Последовательно-параллельные АЦП конвейерного типа

Последовательно-параллельные АЦП занимают промежуточное положение между параллельными и последовательными АЦП по разрешающей способности и быстродействию. Показанный на рис.29.9 АЦП является 12-разрядным двухступенчатым конвейерным, или субинтервальным, преобразователем. Первое преобразование выполняется 6-разрядным АЦП, который управляет 6-разрядным ЦАП. На выходе 6-разрядного ЦАП получается 6-разрядное приближение аналогового входного сигнала. УВХ 2 осуществляет временную задержку аналогового сигнала, пока первый АЦП производит преобразование и ЦАП устанавливает требуемый сигнал на выходе. Затем полученное с помощью ЦАП приближение вычитается из аналогового сигнала на выходе УВХ 2, результат усиливается и оцифровывается вторым 6-разрядным АЦП. Результаты этих двух преобразований объединяются и подаются на выход.

Введение элементов задержки аналогового и цифрового сигналов между ступенями преобразования реализует конвейерный принцип преобразования. Роль аналогового элемента задержки выполняет УВХ 2, цифрового – буферный регистр, который задерживает передачу старших разрядов на один такт.

Конвейерная архитектура значительно увеличивает частоту выборок многоступенчатого АЦП. Это дает возможность без проигрыша в быстродействии увеличивать количество ступеней АЦП, понизив разрядность каждой ступени. Однако, выполнение преобразования за три, четыре или, возможно, даже большее количество конвейерных ступеней вызывает дополнительную задержку выходных данных. Поэтому, если АЦП используется в событийно-управляемом или однократном режиме, требующем однозначного соответствия времени между каждым отсчетом и соответствующими данными, то конвейерная задержка может привести к нежелательному результату. В этом случае более предпочтительна архитектура последовательного или параллельного типа. Конвейерная задержка может создать проблемы в высокоскоростных системах управления с обратной связью или в приложениях с мультиплексированием данных. Кроме того, некоторые конвейерные преобразователи рассчитаны на определенную минимально допустимую скорость преобразования.

Рис.29.9. Конвейерный АЦП

Сигма-дельта АЦП

Когда требуется разрешение лучше 16 двоичных разрядов при высокой частоте выборок, рассматривавшиеся до сих пор методы преобразования становятся недостаточно эффективными, особенно при малых уровнях сигналов. Требование точно откалиброванного многоразрядного ЦАП в качестве элемента схемы преобразования становится чрезмерно жестким. Даже малые отклонения уровней на выходе ЦАП от их номинальных значений, обусловленные разбросом параметров и различное время срабатывания ключей могут привести к провалам в проходной характеристике и даже к пропуску отдельных двоичных комбинаций на выходе.

Сегодняшние скоростные цифровые схемы позволяют создавать преобразователи, действующие по принципу избыточной дискретизации и работающие с частотой выборок, значительно превосходящей теоретический минимум, определяемый шириной занимаемой сигналом полосы. Выгода от применения избыточной дискретизации заключается в том, что спектр шума квантования можно распределить по более широкому интервалу частот. Это дает возможность большую часть шума оставить вне зоны используемых частот при обратной фильтрации дискретизованного сигнала с сохранением компонентов только в полосе исходного сигнала.

Рассмотрим методику избыточной дискретизации с анализом в частотной области. Там, где преобразование постоянного напряжения имеет ошибку квантования до ½ младшего разряда (МЗР), дискретная система, работающая с переменным входным сигналом, обладает шумом квантования. Идеальный классический N-разрядный АЦП имеет среднеквадратичное значение шума квантования, равное h/ 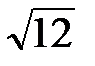. Шум квантования равномерно распределен в пределах полосы Котельникова от 0 до f_В/2 (где h – значение младшего значащего бита и fв— частота дискретизации), как показано на рис.29.9, а. Поэтому, его отношение сигнал/шум для полнодиапазонного синусоидального входного сигнала будет (6,02N+1,76)дБ. Если АЦП несовершенен и его реальный шум больше, чем его теоретический минимальный шум квантования, то эффективная разрешающая способность будет меньше, чем N-разрядов.

Если выбрать более высокую частоту дискретизации K f_В (рис.29.10, а), то среднеквадратичное значение шума квантования остается h / 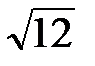, но шум теперь распределен по более широкой полосе от 0 до f_В/2. Если затем использовать на выходе цифровой низкочастотный фильтр, то значительно уменьшится шум квантования, но сохранится полезный сигнал, улучшая таким способом эффективное число разрядов. Таким образом, выполняется аналого-цифровое преобразование с высоким разрешением при использовании аналого-цифрового преобразователя с низкой разрешающей способностью. Коэффициент K здесь упоминается, как коэффициент избыточной дискретизации. При этом необходимо отметить, что избыточная дискретизация дополнительно выгодна еще и тем, что она понижает требования к аналоговому ФНЧ.

Так как ширина полосы пропускания уменьшена выходным цифровым фильтром, скорость выдачи выходных данных может быть ниже, чем первоначальная частота дискретизации (K_fВ), и при этом все же удовлетворять теореме Котельникова. Это достигается посредством передачи на выход каждого М-го результата и отбрасывания остальных результатов. Такой процесс называют децимацией с коэффициентом М. Несмотря на происхождение термина (decem по-латыни — десять), М может принимать любое целое значение, при условии, что частота выходных данных больше, чем удвоенная ширина полосы сигнала. Прореживание не вызывает никакой потери информации (см. рис.29.10, б).

Если использовать избыточную дискретизацию только для улучшения разрешающей способности, необходимо применять коэффициент избыточности 2^2N, чтобы получить N- разрядное увеличение разрешающей способности. Сигма-дельта (Σ∆) преобразователь не нуждается в таком высоком коэффициенте избыточной дискретизации. Он не только ограничивает полосу пропускания сигнала, но также задает форму кривой распределения шума квантования таким образом, что большая ее часть выходит за пределы этой полосы пропускания, как это показано на рис.29.10, в.

Рис.29.10. Спектры шумов квантования в простом АЦП (а), АЦП с избыточной дискретизацией, цифровым фильтром и децимацией (б) и Σ∆-АЦП с избыточной дискретизацией, цифровым фильтром и децимацией (в)

В методе избыточной дискретизации типичное значение коэффициента избыточности составляет 256 и более. Применяя обработку, обеспечивающую оптимальное формирование спектра шума, можно достичь разрешения в 18 бит и более при 1-разрядном преобразователе (1-разрядный АЦП – обыкновенный аналоговый компаратор).

Отличительной чертой 1-разрядного АЦП по сравнению с многоразрядными преобразователями является то, что в нем одни и те же аналоговые компоненты используются многократно в течение интервала времени между появлением выборок на выходе. Аналоговое входное напряжение преобразуется в цифровые биты по принципу повторного использования компонентов снова и снова, а не посредством применения различных элементов, относящихся к различным значениям, как это делается в многоразрядном преобразователе. Большая тактовая частота, с которой осуществляются повторения, позволяет достичь высокой точности, несмотря на разброс элементов компонентов.

Если посмотреть на сигнал, прошедший 1-разрядное преобразование, на частоте, равной частоте взятия выборок при избыточной дискретизации, то можно увидеть повышенную концентрацию двоичных единиц, когда аналоговый сигнал имеет большое значение, и повышенную концентрацию нулей, когда величина напряжения на входе мала.

На рис.29.11 представлена функциональная схема Σ∆-АЦП. Дифференциальный усилитель на входе непрерывно сравнивает входной сигнал с напряжением на выходе 1-разрядного ЦАП, который в типичном случае работает на частоте в 256 раз большей, чем требуемая частота окончательных выборок на цифровом выходе. Например, при частоте окончательных выборок 44,1 кГц тактовая частота внутренней избыточной дискретизации должна равняться 11,2896 МГц. Сигнал с выхода дифференциального усилителя интегрируется и подается на компаратор, а выходной сигнал компаратора стробируется с частотой избыточной дискретизации. Если сигнал на выходе интегратора больше 0 В, то на выходе компаратора идет поток двоичных единиц, а если оно меньше 0 В, то результатом будет последовательность нулей. Компаратор, по существу, является 1-разрядным АЦП, и он генерирует последовательность единиц и нулей в соответствии с результатом интегрирования выходного сигнала дифференциального усилителя.

Рис.29.11. Σ∆-АЦП

Петля обратной связи замыкает путем подачи стробированного сигнала с выхода компаратора на вход 1-разрядного ЦАП. Это приводит к тому, что на выходе дифференциального усилителя возникает разность между мгновенным значением напряжения на аналоговом входе и средним значением аналоговых выборок, непосредственно предшествующих данному моменту времени. Петля ЦАП – дифференциальный усилитель – компаратор поддерживает нулевой заряд на конденсаторе интегратора. На стробированном выходе компаратора каждый раз появляется достаточное количество со значением «логическая 1», чтобы компенсировать заряд, поступивший в интегратор со стороны аналогового входа через дифференциальный усилитель. Другими словами, на выходе логического элемента И возникает поток битов, следующий с высокой частотой (в типичном случае – 11,2896 МГц), причем плотность логических единиц пропорциональна напряжению на аналоговом входе.

Чтобы выполнить преобразование потока битов в двоичное число, можно воспользоваться счетчиком и регистром-защелкой. На практике это выполняется с помощью цифрового фильтра нижних частот, на выходе которого вновь берутся выборки с частотой 44,1 кГц. Фильтр нижних частот сглаживает быстрые изменения в цифровом сигнале и, следовательно, осуществляет усреднение его по времени, подготавливая сигнал к тому, чтобы из него вновь могли быть взяты выборки с требуемой частотой. Эта процедура называется прореживанием или децимацией.

Дополнительный выигрыш, получаемый от применения избыточной дискретизации, состоит в том, что исключаются сложные аналоговые фильтры, необходимые для того, чтобы избежать перекрытия спектров.

Сегодняшние высокоскоростные средства обработки сигналов позволяют сделать преобразователи с избыточной дискретизацией не только более точными, чем многоразрядные схемы, но и более дешевыми, поскольку вместо трудно осуществимой точности значений параметров здесь требуется точность стробирования, а это значительно проще. Избыточная дискретизация в большой степени терпима к несовершенствам аппаратных средств. В общем случае, отпадает необходимость схемы выборки-хранения, поскольку частота преобразования входного сигнала исключительно велика по сравнению с частотой аналогового входного сигнала.

Недостатком сигма-дельта АЦП является то, что при скачкообразном изменении входного сигнала они начинают давать результат только через три – четыре отсчета.

В настоящее время ряд ведущих фирм-производителей АЦП полностью перешли в области аналого-цифрового преобразования высокого разрешения на сигма-дельта АЦП. Эти АЦП имеют развитую цифровую часть, включающую микроконтроллер. Это позволяет реализовывать режимы автоматической установки нуля, самокалибровки полной шкалы, хранить калибровочные коэффициенты и передавать их по запросу внешнего процессора.

С внедрением усовершенствованных АЦП и ЦАП различие между аналоговыми и цифровыми сигналами становится почти незаметным. Конечно, нужно позаботиться о том, чтобы избежать перекрестных искажений при взаимодействии аналоговой и цифровой частей в схеме, но преобразование сегодня все в большей степени сводится просто еще к одной интегральной микросхеме на печатной плате. Это способствует тому, что цифровая обработка сигналов применяется для выполнения все новых и новых функций в электронике.