Эффективность без цен

Эффективность в обмене

Рассмотрим модель, в которой происходит распределение фиксированного количества благ между индивидами. В этой модели количества благ заданы заранее, и изменения благосостояния индивидов могут иметь место только в результате обмена. Поэтому данную модель называют "экономикой обмена". Существует условие эффективности в обмене, которое мы можем сформулировать сразу: блага размещены эффективно, если предельные нормы замены между любыми двумя благами одинаковы для всех индивидов.[2]

Представим, что происходит обмен двумя благами между индивидами - Андреем и Борисом. Формально условие эффективности в обмене можно записать как:

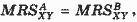
где MRS^A_XY - предельная норма замены блага Y благом X для Андрея; MRS^B_XY- предельная норма замены блага Y благом X для Бориса. Любое распределение этих благ между Андреем и Борисом, при котором не выполняется это равенство, является парето-неэффективным (т. е. их благосостояние может быть улучшено).

Покажем справедливость этого утверждения. Пусть благо X, имеющееся в количестве 50 ед., и благо Y, имеющееся в количестве 100 ед., распределены между Андреем и Борисом поровну. При этом предельные нормы замены не равны: у Андрея MRS^A_XY = 2 (он готов отдать 2 ед. X за единицу Y), а у Бориса MRS^B_XY = 1. Легко заметить, что индивиды могут улучшить свое благосостояние путем обмена. Если взять 1 ед. X у Бориса и передать ее Андрею, забрав у него 2 ед. Y, то благосостояние Андрея не изменится. Если из полученных 2 ед. Y отдать Борису, то его благосостояние тоже останется таким же, как и до обмена. Таким образом, новое распределение (Андрей имеет 26 ед. X и 48 ед. Y, а Борис - 24 ед. X и 51 ед. Y) приносит такое же количество полезности индивидам, что и ранее, но 1 ед. блага Y остается свободной. Если отдать ее Андрею или Борису, то произойдет парето-улучшение и уровень их благосостояния увеличится. Следовательно, первоначальное распределение было неэффективным.

Отсюда вытекает, что при любом размещении с разными нормами замены благосостояние может быть увеличено путем перераспределения благ (обмена) между индивидами.

Приведем более строгое доказательство условия эффективности в обмене:

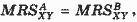
Задача заключается в том, чтобы максимизировать полезность одного индивида, скажем А, в то время как полезность другого, B,, принимается фиксированной на постоянном уровне, скажем Ü^B .

Индивидуальные функции полезности заданы как:

U^A = U^A(X,Y),

U^B = U^B(X,Y),

где X и Y, как и ранее, блага в экономике обмена, состоящей из двух индивидов и двух благ. Сформируем функцию Лагранжа:

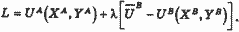
Дифференцируя L по Х и Y и приравнивая полученные выражения к нулю, имеем:

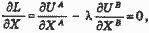
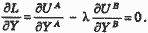
После ряда преобразований и вспомнив теорию потребления, получаем:

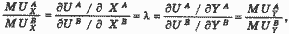
где MU - предельная полезность. В итоге небольших перестановок приходим к следующему результату:

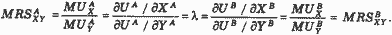
В рассматриваемой нами экономике обмена может иметь место множество различных парето-эффективных размещений. Для двух субъектов и двух благ это можно наглядно продемонстрировать с помощью так называемой коробки Эджуорта (рис. 2).

Горизонтальная сторона этой коробки показывает общее количество блага X, а вертикальная - общее количество блага Y. Точка О_А является началом координат для Андрея, а точка О_B - для Бориса. Любая точка внутри коробки характеризует размещение благ Х и Y между индивидами. Например, в точке G Андрей обладает количеством блага X^G_А блага X и количеством блага Y^G_А, блага Y, Борис обладает оставшимися количествами этих благ соответственно X^G_Bи Y^G_B.

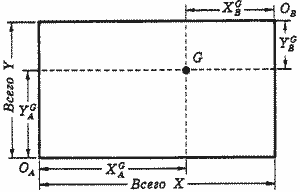
Рис. 2. Диаграмма "коробка Эджуорта".

Таким образом, множество точек внутри коробки Эджуорта представляет все возможные способы размещения двух благ между двумя индивидами. Какие же точки из этого множества являются парето-эффективными?

Чтобы ответить на этот вопрос, мы должны знать предпочтения индивидов. Поскольку коробка Эджуорта представляет собой для каждого индивида пространство благ, для изображения предпочтений мы воспользуемся картой безразличия. Кривые безразличия для Андрея обозначаются буквами U_А, они выпуклы по отношению к его началу координат O_А, и увеличение полезности означает переход на более высокие кривые (рис. 3). Кривые безразличия для Бориса обозначаются буквами U_B, они выпуклы по отношению к его началу координат О_B, а увеличение полезности означает переход на более низкие кривые (карта предпочтений Бориса в нашей коробке как бы перевернута на 180°).

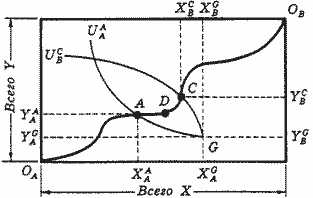
Рис. 3. Эффективность в обмене.

Используя эти кривые безразличия, можно найти точки парето-эффективных размещений.

Парето-эффективное размещение наблюдается тогда, когда при заданном уровне полезности одного индивида другой получает максимально возможный уровень полезности. Это означает, что на каждой кривой безраличия одного из индивидов нужно найти точку, в которой полезность другого индивида максимальна. Например, для кривой безразличия Бориса U^D_B - это точка D, точка касания самой высокой кривой безразличия Андрея. Любая другая точка на кривой U^D_B, например точка K, не будет парето-эффективной, так как, перемещаясь по направлению к точке D, мы будет увеличивать уровень полезности Андрея, не изменяя уровень полезности Бориса.

Нетрудно понять, что множество точек касания кривых безразличия Андрея с кривыми безразличия Бориса задает все возможные парето-эффективные размещения между индивидами. Заметим, что во всех этих точках выполняется сформулированное ранее условие эффективности в обмене - предельные нормы замены Андрея и Бориса равны, так как равны наклоны кривых безразличия в точках их касания.

Множество этих точек составляет контрактную кривую - на рис. 3 это линия, соединяющая точки О_A и О_B. Поскольку каждое размещение на этой кривой парето-эффективно, при перемещении по контрактной кривой увеличение полезности одного индивида достигается только за счет уменьшения полезности другого. Поэтому контрактную кривую называют также конкурентной.

Этого нельзя сказать о точках вне контрактной кривой. Например, точка G не является парето-эффективным размещением, так как из нее индивиды могут переместиться в другую точку (например, в точку D), увеличив полезность каждого.

Заметим, что контрактная кривая является аналогом кривой возможных полезностей, только в первом случае на осях откладываются количества благ, а во втором - уровни полезности индивидов, получаемые от наборов благ. Если предположить, что уровень полезности измерим количественно, мы сможем построить рис. 1 по данным об уровнях полезности на контрактной кривой на рис. 3. Без введения количественной меры полезностей наборов благ X и Y о форме этой кривой нельзя сказать ничего определенного, и поэтому кривую возможных полезностей, как правило, изображают не имеющей постоянного знака выпуклости. Единственное, что можно сказать определенно, так это то, что она должна иметь отрицательный наклон. Ведь увеличение уровня поезности одного индивида может произойти только за счет снижения уровня полезности другого (при условии парето-эффективного размещения).

Предположим теперь, что существует некоторое изначальное наделение (endowment) индивидов благами, которое является случайным; например, Андрей и Борис оказались после кораблекрушения на необитаемом острове, причем каждый сумел захватить с собой с тонущего корабля некоторое количество блага X и некоторое количество блага Y.

Маловероятно, что получившееся распределение благ будет парето-эффективным.

Попробуем сделать выводы о возможных вариантах добровольного обмена.

Следовательно, Андрей и Борис могут увеличить свою полезность, обменявшись некоторым количеством благ, и эта возможность улучшить свое положение побудит их вступить в обмен добровольно. Какими могут быть условия этого добровольного обмена?

Мы можем определить множество возможных вариантов обмена исходя из предположения, что ни один из индивидов не станет заключать сделки, если его положение ухудшится. Предположим, что исходное размещение представлено точкой G, которая не является парето-эффективной (рис. 4). Выбирая вариант обмена, Андрей не согласится на уровень полезности ниже U^A_A, а Борис не согласится на уровень полезности ниже U^C_B. Отсюда следует, что сделка будет заключена только в том случае, если новое состояние окажется где-то внутри области, заключенной между кривыми безразличия U^A_A и U^C_B.

Рис. 4. Эффективность в обмене и исходная неэффективная аллокация.

Обсуждая условия сделки, Андрей и Борис могут найти парето-эффективное состояние, если выберут точку на участке АС, принадлежащем контрактной кривой. Но какую именно точку они должны будут выбрать, определить невозможно. Все точки на участке АС представляют собой состояния, после достижения которых дальнейшее добровольное перезаключение сделок невозможно, так как один из индивидов будет что-то при этом терять. Андрей будет стремиться к тому, чтобы эта точка была поближе к точке С, Борис будет стремиться к тому, чтобы эта точка была поближе к точке А. Результат этого "перетягивания каната" не будет определен до тех пор, пока не будут сделаны какие-то дополнительные предположения о поведении индивидов. Заметим, что этот анализ по сути дела аналогичен анализу двусторонней монополии, которая также не имеет единственно возможного равновесия, а имеет только диапазон возможных цен сделки.

Однако анализ экономики обмена с двумя индивидами и двумя благами представляет собой лишь иллюстрацию на частном примере основных понятий экономики обмена. В дальнейшем, при анализе экономики с использованием механизма цен, мы убедимся в единственности равновесия, и этот вывод можно будет распространить на произвольное число субъектов.

Эффективность в производстве

Парето-эффективоность в производстве означает, что нельзя увеличить выпуск одного блага без того, чтобы в результате не сократился выпуск какого-либо другого блага.

Предположим, что фирма использует два вида ограниченных ресурсов (капитал - K и труд - L) для выпуска двух разных благ (Х и Y). Вариант производства парето-эффективен, если невозможно перегруппировать ресурсы таким образом, чтобы увеличить выпуск блага Х без сокращения выпуска Y. Для этого необходимо выполнение условия:

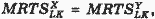
где MRTS^X_LK - предельная норма технической замены трудом капитала в производстве блага X, а MRTS^Y_LK - предельная норма технической замены трудом капитала в производстве блага Y.

Пусть фирма располагает 100 чел.-ч и 100 маш.-ч, которые она может распределить между производством пылесосов (X) и холодильников (Y). Допустим, фирма решила половину из каждого ресурса направить на производство пылесосов, а другую половину - на производство холодильников. Предельные нормы технической замены для этих продуктов будут при этом различаться: в производстве пылесосов MRTS^X_LK = 2, а в производстве холодильников MRTS^Y_LK = 1. Легко показать, что при таких значениях MRTS размещение ресурсов парето-неэффективно. Если мы заберем 1 чел.-ч из производства холодильников и пустим его на производство пылесосов, то из производства пылесосов мы сможем забрать 2 маш.-ч без уменьшения выпуска последних. Из этих 2 маш.-ч один нам нужно будет "вернуть" в производство холодильников, чтобы компенсировать изъятие 1 чел.-ч, а 1 маш.-ч остается "лишним" и может быть использован для увеличения производства одного из благ без уменьшения производства другого. Таким образом, нераспределение ресурсов приводит к парето-улучшению. Попытаемся проиллюстрировать вышесказанное с помощью рис. 5, на котором изображена коробка Эджуорта для производства.

Вертикальная сторона показывает общее количество доступного фирме капитала, горизонтальная сторона - труда. Точка O_X является началом координат для карты изоквант, показывающих различные уровни выпуска блага Х, которые могут быть произведены с использованием различных комбинаций ресурсов K и L. Точка O_Y является началом координат для карты изоквант блага Y.

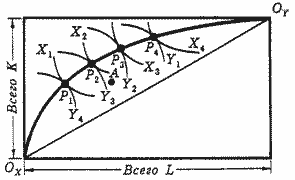
Рис. 5. Эффективные размещения ресурсов внутри одной фирмы.

Любая точка в коробке представляет размещение обоих ресурсов между производством Х и Y. Местоположение парето-эффективных способов размещения K и L представлено точками (P₁,...,P₄) касания изоквант производства X (X₁,...,X₄) и изоквант производства Y (Y₄,...,Y₁). Множество всех таких точек касания образует линию O_XO_Y, аналогичную контрактной кривой. Во всех точках линии O_XO_Y предельные нормы замены для обоих продуктов равны.

В соответствии с условием эффективности в производстве:

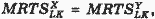
Задача заключается в том, чтобы максимизировать количество блага Х при данном уровне выпуска блага Y, скажем , и располагаемом количестве капитала и труда (K и L). Нижние индексы X и Y указывают продукцию, на производство которой направлен соответствующий ресурс. Таким образом, имеются ресурсные ограничения:

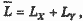
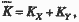
производственные функции:

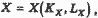
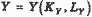
и цель максимизировать при ограничении:

Cоставляем функцию Лагранжа:

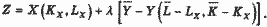
Дифференцируем по K_X и L_X и приравниваем к нулю:

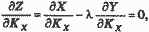
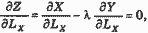
так что:

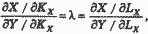
и в итоге имеем:

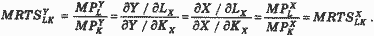
Точки вне линии O_XO_Y (например, точка А) парето-неэффективны. Переместившись из точки А на линию O_XO_Y (например, в точку P₂), фирма может произвести больше и блага X, и блага Y.

Поскольку линия O_XO_Y показывает максимальный выпуск Y, который может быть осуществлен при любом данном выпуске Х, эту информацию можно использовать для построения границы производственных возможностей, которая показывает альтернативные комбинации благ, которые могут быть произведены при данном количестве эффективно используемых ресурсов. Эту границу называют линией трансформации: она показывает, как один продукт "трансформируется в другой" путем переключения ресурсов с производства одного блага на производство другого. На рис. 6 такая граница производственных возможностей (T_XT_Y) построена для благ Х и Y на основе рис. 5. Данные о выпуске благ X и Y "считаны" с соответствующих касающихся друг друга изоквант и представлены на осях. Точки P₁,P₂,P₃,P₄ на рис. 6 соответствуют аналогичным точкам на рис. 5. Точка А по-прежнему показывает неэффективность в производстве, которая становится более наглядной на рис. 6 (в результате неэффективного размещения ресурсов фирма не дотягивает до границы производственных возможностей).

Заштрихованная область показывает уровни выпуска благ X и Y, являющиеся предпочтительными по отношению к их выпуску относительно точки А.

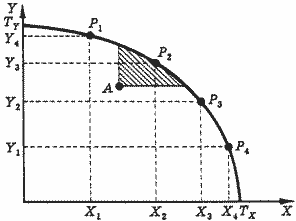
Рис. 6. Граница производственных возможностей.

Наклон границы производственных возможностей показывает, в какой пропорции выпуск одного блага может быть заменен выпуском другого блага при условии, что общее количество используемых ресурсов остается постоянным и применяется эффективно.

Величина, показывающая, на сколько единиц нужно сократить производство одного блага, чтобы увеличить производство другого на единицу, называется предельной нормой трансформации:

Заметим, что трансформация одного продукта в другой происходит не в результате обмена, а в результате изменения структуры выпуска вследствие перемещения ограниченных ресурсов между производством одного и другого продуктов.

Предполагается, что граница производственных возможностей вогнута к началу координат. Это означает, что при увеличении выпуска блага X (и соответствующем уменьшении выпуска блага Y) предельная норма трансформации MRT_XY возрастает: для увеличения выпуска X на единицу приходится жертвовать все большими количествами Y.

Если один ресурс является "более подходящим" для производства, скажем, блага Х, чем для блага Y (и наоборот), то тогда вогнутая форма границы производственных возможностей также может быть объяснена. В этом случае увеличение выпуска блага X требует привлечения все менее подходящих для этого ресурсов. Предельные издержки блага Х возрастали бы, тогда как, с другой стороны, предельные издержки блага Y уменьшались бы по мере сокращения выпуска, так как в его производстве оставались бы все более пригодные ресурсы. Однако такое объяснение приходит в противоречие с предпосылкой об однородности ресурсов, которая занимает важное место в микроэкономическом анализе. Даже если ресурсы однородны и производственные функции характеризуются постоянной отдачей от масштаба, граница производственных возможностей будет вогнутой при условии, что в производстве благ Х и Y ресурсы используются в различных пропорциях.[3] В диаграмме на рис. 5 благо X является капиталоинтенсивным по отношению к благу Y. Так, в каждой точке линии O_XO_Y отношение K к L в производстве блага Х превышает отношение K к L в производстве блага Y: дугообразная линия O_XO_Y постоянно находится выше диагонали. Если бы, напротив, благо Y было капиталоинтенсивным, то дугообразная линия O_XO_Y всегда располагалась бы ниже диагонали. Когда комбинации благ Х и Y перемещаются слева направо по O_XO_Y (рис. 5), то соотношение капитал-труд уменьшается в производстве обоих благ. Однако, так как благо X капиталоинтенсивное, такое изменение данного соотношения увеличивает MC_X.

В то же время, поскольку благо Y трудоинтенсивное, это же изменение приводит к тому, что MC_Y падает. Следовательно, относительные предельные издержки блага Х увеличиваются, что и показывает вогнутая форма границы производственных возможностей на рис. 6. До сих пор в нашей модели присутствовала одна фирма. Если фирм больше, то рассмотренное условие эффективности в производстве дополняется еще двумя.[4]

Эффективность структуры продукции

Для достижения полной парето-эффективности экономики условия эффективности как в производстве, так и в обмене должны выполняться одновременно. Парето-эффективность в производстве и обмене предполагает такой выбор структуры продукции, когда предельная норма замены для любых двух благ (нормы замены равны для всех индивидов, если имеет место парето-эффективность в обмене) равна предельной норме трансформации этих двух благ (нормы трансформации равны для всех фирм, если имеет место парето-эффективность в производстве). Для варианта с двумя индивидами (А и В) и двумя благами (Х и Y) это можно формально записать следующим образом:

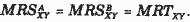
Допустим, что индивиды желают обменять 2 яблока на 1 грушу, но ресурсы размещены так, что только 1 яблоко могло бы быть заменено в производстве на 1 грушу. В этом случае парето-эффективность структуры продукции не достигнута. В этой ситуации производится слишком мало груш, так как индивиды оценивают груши выше: по условиям производства выращивание одной дополнительной груши потребовало бы отказа от 1 яблока, но наши индивиды готовы пожертвовать 2 яблоками за 1 грушу. Когда пропорция, в которой индивиды желают обменивать блага, отличается от пропорции, в которой они могут это сделать, возможно парето-улучшение. Эффективность структуры продукции показана на рис. 7. С внутренней стороны границы производственных возможностей T_XT_Y расположена коробка Эджуорта (О_А и О_B, как и на рис. 3, представляют начала координат, относительно которых строятся карты безразличия Андрея и Бориса), демонстрирующая достижение эффективности в обмене в точке D.

Если угол наклона кривых безразличия в точке их касания равен углу наклона границы производственных возможностей в точке P_D, то парето-эффективность в обмене сочетается с парето-эффективностью в производстве (предполагается, что у всех фирм одинаковы, а сам факт нахождения на границе производственных возможностей свидетельствует о соответствии всем остальным условиям парето-эффективности в производстве).

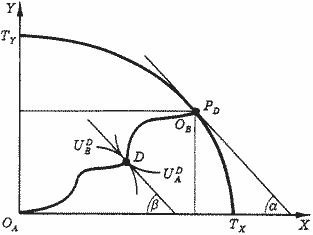
Рис. 7. Эффективность структуры продукции. Угловые коэффициенты: α = MRT_XY = MC_X / MC_Y; α = MRS^A_XY = MRS^B_XY = (MU_X/ MU_Y)^A / (MU_X/ MU_Y)^B.

Иногда эффективность структуры продукции представляют с помощью модели, которая называется "экономика Робинзона". В этой модели один индивид (Робинзон) производит и потребляет два блага (X и Y). Поскольку мы имеем дело с функцией полезности одного индивида, оптимальная структура продукции будет иметь место там, где индивидуальная кривая безразличия (U₂) касается границы производственных возможностей (рис. 8). В точке Е достигается максимальная полезность для Робинзона (эффективность в обмене тождественна эффективности в потреблении), тогда как нахождение на границе производственных возможностей означает эффективность в производстве.

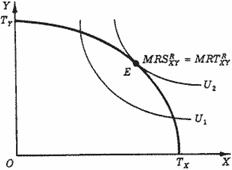
Рис. 8. Эффективность структуры продукции в "экономике Робинзона".

^[2] Это условие справедливо только для случая, когда индивиды потребляют оба блага. В случае "углового решения" (когда индивиды предпочитают потреблять лишь какое-либо одно благо) предельные нормы замены могут быть не равны при эффективной аллокации. В данной лекции угловые решения не рассматриваются (это относится и к излагаемой далее проблеме эффективности в производстве).

^[3] Если при однородных ресурсах и постоянной отдаче от масштаба в производстве каждого из благ ресурсы K и L используются в одинаковой пропорции при эффективной их аллокации, то граница производственных возможностей будет прямой линией.

^[4] Первое условие состоит в следующем: если производство эффективно, то ресурсы должны быть размещены таким образом, чтобы предельные продукты данного ресурса в производстве одного и того же блага были равны между собой независимо от того, какая фирма производит это благо. В случае для двух фирм (фирма 1 и фирма 2) и одного ресурса (допустим, труда) его можно записать как MP¹_L = MP²_L.
Второе условие: если фирмы производят одни и те же блага, то они должны выбирать такие комбинации этих благ на границах производственных возможностей, где их предельные нормы трансформации равны. Для тех же двух фирм и продуктов X и Y его можно записать как . Это равенство говорит об отсутствии сравнительных преимуществ между фирмами в производстве продуктов х и y, т. е. относительные издержки производства этих благ одинаковы у обеих фирм.