Способы измерения дифференциации доходов. Кривые Лоренца
Как велико неравенство доходов различных групп населения? Каким образом количественно оценить степень дифференциации доходов? Каково соотношение групп населения с относительно высокими и относительно низкими доходами? Какие статистические показатели имеются в нашем распоряжении?
Показатель среднего дохода, исчисленный как средняя арифметическая, очень чувствителен к увеличению или уменьшению доли высокодоходных или низкодоходных групп населения. В статистике большинства развитых стран для характеристики общего уровня доходов приводится не средний, а медианный их уровень, т. е. уровень, выше и ниже которого получает доход одинаковое число работников. Еще одной характеристикой, применяемой при исследовании доходов, является мода, представляющая собой наиболее распространенный уровень дохода.
Пусть, например, необходимо найти средний доход для совокупности из семи работников.
Мы можем действовать несколькими способами. Во-первых, просуммировав все доходы и поделив найденную величину на 7, мы получим среднюю арифметическую доходов. Во-вторых, проранжировав работников в порядке возрастания (или убывания) доходов, за средний доход мы можем принять доход работника, занимающего в ранжированной совокупности четвертую позицию, т. е. доход, выше и ниже которого получает доходы одинаковое число единиц данной совокупности (по три работника). В этом случае мы имеем дело с медианным уровнем дохода, отличие которого от среднего арифметического уровня заключается в том, что он характеризует действительный доход среднего человека, а не средний доход абстрактного человека. И наконец, в-третьих, за средний доход мы можем принять наиболее часто встречающийся в данной совокупности уровень дохода; если, например, у двух работников доходы совпадают, а у всех остальных различны, то данный уровень дохода можно считать средним для всей совокупности. Этот доход и получил название модального дохода. Таким образом, численное значение моды попадает в интервал дохода, которому соответствует наибольшая частота, или доля населения, получающая данный доход.
Таблица 1. Доходы населения в СССР: средний, медианный и модальный уровни (руб./мес.)
| Доход | |||||
| Средний Медианный Модальный | 109,6 101,9 89,0 | 125,8 116,6 89,1 | 141,2 132,8 112,5 | 149,6 140,8 118,2 | 164,6 158,0 133,8 |
Примечание. Рассчитано по данным статистических ежегодников “Народное хозяйство СССР” за 1988, 1989, 1990 гг.
На основе данных Госкомстата СССР о распределении населения по среднедушевому совокупному доходу попробуем сравнить показатели среднего, медианного и модального доходов (табл. 1). Из таблицы видно, что средний доход по абсолютной величине превосходит медианный и модальный доходы, причем рост его происходит в основном за счет увеличения доли лиц, имеющих высокие доходы, т. е. использование показателя среднего дохода приводит к существенному завышению уровня доходов основной массы населения и в значительной мере скрывает процесс их дифференциации. Значения модального дохода тяготеют к нижним группам распределения и отклоняются от медианного дохода в меньшую сторону. Однако попадание моды в тот или иной интервал зачастую носит случайный характер: достаточно небольшого изменения в распределении — и мода окажется уже в соседнем интервале. Например, в 1989 г. наиболее распространенным являлся уровень дохода от 100 до 125 рублей (такой доход получали 16.1 % населения), однако ввиду незначительных сдвигов в доходах, происшедших за 1989—1990 гг., наиболее распространенным интервалом оказался следующий интервал (125—150 руб.), а само значение моды возросло на 15.6 руб. Кроме того, доля населения в модальном интервале дохода может превышать другие доли весьма незначительно.
Однако все эти характеристики по-прежнему не позволяют ответить на вопрос о том, во сколько раз доходы одних групп населения превышают доходы других. В этом отношении анализ доходов целесообразно дополнить характеристиками, измеряющими разрыв между высокодоходными и низкодоходными группами населения. Такими характеристиками могут являться децильные, квартальные, квантильные и другие коэффициенты, которые подразумевают разбиение исходной совокупности на равные части и измеряют соотношение между доходами двух крайних групп. Если все население разбить на четыре группы и найти отношение среднего дохода последней группы (т. е. той четверти населения, которая имеет наиболее высокие доходы) к среднему доходу первой группы (т. е. группы, включающей низкодоходные слои населения), то мы получим квартальный коэффициент дифференциации доходов. Аналогично, разбив исходную совокупность на пять частей и найдя отношение среднего дохода последней группы к первой, получим квантильный коэффициент дифференциации. При нахождении же децильных коэффициентов совокупность разбивается на 10 равных групп (частей).
Еще один интересный прием анализа доходов населения с точки зрения их дифференциации состоит в расчете так называемых накопленных, или кумулятивных, частот (долей) и построении кумулятивных кривых, или кривых Лоренца (по имени американского статистика М. Лоренца). Рассмотрим на простом примере, как строится кривая Лоренца.
Четыре индивида (назовем их А, В, С и D) получают суммарный доход в 10000 руб. в месяц, который распределяется между ними в соответствии с данными табл. 2. Ясно, что такое распределение дохода не является равномерным. Подсчитав удельный вес дохода каждого индивида в общем доходе, мы можем сказать следующее: наименьшую долю дохода (10 %) получает А; А и В получают 10 + 15 = 25 % дохода, или, иными словами, одна половина людей получает четвертую часть, а другая — три четверти общего дохода.
А, B и С получают 10 + 15 + 30 = 55 % дохода, т. е. на долю D приходится 45 % общего дохода. Полученные последовательным суммированием долей новые удельные веса и называются накопленными, или кумулятивными, частотами. Графически изобразить и измерить неравенство доходов можно с помощью кривой Лоренца. Для ее построения отложим по оси абсцисс последовательно просуммированные удельные веса индивидов в их общем числе, учитывая, что удельный вес каждого из них составляет одну четверть, или 25 %, а по оси ординат — кумулятивные доли доходов этих людей. Соединив все точки, получим кривую Лоренца (рис. 3).
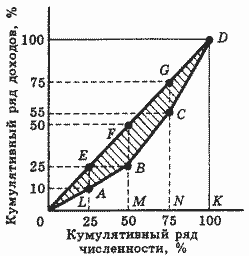
Рис. 3. Кривая распределения доходов четырех индивидов
| Таблица 2. Распределение дохода между четырьмя индивидами
|
Чтобы понять, каким образом эта кривая отражает неравенство доходов, попытаемся ответить на вопрос: какой бы вид имела кривая Лоренца в случае полного равенства доходов? Очевидно, что в такой ситуации каждый получал бы 2500 руб. дохода, т. е. ордината точки А переместилась бы в точку Е, точки B — в точку F и т. д., следовательно, мы получили бы прямую OD, составляющую с осями координат угол в 45о. Таким образом, неравенство доходов характеризуется степенью отклонения кривой Лоренца от биссектрисы 1-го координатного угла. Это отклонение можно измерить через отношение площади заштрихованной фигуры между кривой Лоренца и прямой OD к площади всего треугольника ODK. В результате получим показатель, который в литературе называется коэффициентом концентрации (или коэффициентом Джини (по имени итальянского статистика и экономиста К. Джини)):
G = площадь ODBCA/площадь ODK.
Попробуем рассчитать значение данного коэффициента для нашего примера. Площадь фигуры ODCBA можно с определенной степенью точности найти вычитанием из площади треугольника ODK суммы площадей треугольника OAL и трапеций ABML, BCNM и CDKN, основания которых численно равны накопленным частотам доходов, а высоты — соответствующим удельным весам индивидов. Таким образом, имеем:
| ODK = 100.100 = 5000, |
| OAL = 25.10= 125, |
| ABML = 25 = 437.5, |
| BCNM = 25 = 1000, |
| CDKN = 25 = 1937.5. |
Просуммировав соответствующие площади, получим, что площадь фигуры ODCBA составит 5000 – 3500 = = 1500, поэтому значение коэффициента концентрации для нашего примера будет равно:
| G = 1500/5000 = 0.3. |
Очевидно, что чем ближе значение этого коэффициента к единице, тем выше дифференциация доходов, и, наоборот, чем ближе его значение к нулю, тем более равномерным является распределение доходов.
Обратимся к данным табл. 3, характеризующим распределение населения СССР по среднедушевому совокупному доходу в 1990 г. и попробуем на основе этих данных построить кривую Лоренца и вычислить значение коэффициента Джини. Однако здесь мы сталкиваемся с некоторыми трудностями. Как видно из предыдущего примера, для построения кривой Лоренца и расчета коэффициента Джини необходимы данные о доле дохода каждой группы населения в совокупном доходе. Эти данные в табл. 3 отсутствуют (в нашей стране они до сих пор не публикуются). Поэтому, чтобы получить некоторое приближение к такому распределению, воспользуемся простым приемом [8]: (см. табл. 3): умножим средние для каждого интервала доходы (определим их как середину интервала) на соответствующие удельные веса (доли) населения, получив тем самым так называемые процентные числа групповых доходов (табл. 3). Затем, рассчитав удельные веса групп в общем доходе и просуммировав их, получим кумулятивный ряд по доходам, выраженный в процентах.
Таблица 3. Распределение населения СССР по среднедушевому совокупному доходу в 1990 г. и расчет накопленных частот
| Доход, руб. | Середина интервала, руб. | Удельный вес населения, % | Кумулятивный ряд численности, % | Групповые доходы (процентные числа) (2<+3) | Удельный вес групп в общем доходе, % | Кумулятивный ряд доходов (накопленные частоты), % |
| До 50 50-75 75-100 100-125 125-150 150-175 175-200 200-250 250 и более | 37,5 62,5 87,5 112,5 137,5 162,5 187,5 225,0 275,0 | 108 5,9 10,6 13,7 14,3 13,2 10,8 14,9 14,8 | 1,8 7,7 18,3 32,0 46,3 59,5 70,3 85,2 100,0 | 67,5 368,75 927,50 1 541,25 1 966,25 2 145,00 2 025,00 3 352,50 4 070,00 | 0,4 2,2 5,6 9,4 11,9 13,0 12,3 20,4 24,8 | 0,4 2,6 8,2 17,6 29,5 42,5 54,8 75,2 100,00 |
| Всего | — | 100,0 | — | 16 463,75 | 100,0 | — |
Источник: СССР в цифрах в 1990 году : Краткий статистический сборник. М., 1991. С. 129.
Нанесем на график точки, абсциссы которых соответствуют кумулятивному ряду численности населения, рассчитанному путем суммирования соответствующих удельных весов населения, а ординаты — кумулятивному ряду доходов (рис. 4). В результате получим кривую Лоренца, отражающую распределение доходов различных групп населения.
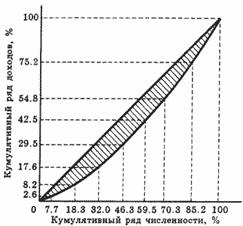
Рис. 4. Кривая распределения доходов населения в СССР в 1990 г.
Теперь мы можем рассчитать значение коэффициента концентрации для данной кривой. Просуммировав соответствующие площади, получим, что площадь заштрихованной фигуры составит 5000 – 3846 = 1154, поэтому значение коэффициента концентрации в данном случае будет:
| G = 1154/5000 = 0.231. |
С помощью кривых Лоренца можно также наглядно продемонстрировать процесс выравнивания доходов через проведение мер налоговой и социальной политики. Так, например, с более высоких доходов при прогрессивном налогообложении взимается более высокий налог, а такие правительственные программы, как социальное страхование, выплата различных пособий, продовольственная помощь, увеличивают доходы относительно бедных слоев населения. При наличии соответствующих данных можно построить кривые Лоренца, отражающие уровни доходов до выплаты налогов, доходов за вычетом налогов и доходов после получения различных выплат и пособий в соответствии с социальными программами (рис. 5), и, сравнив соответствующие коэффициенты концентрации, сделать выводы о влиянии проводимой налоговой и социальной политики на процесс выравнивания доходов населения.
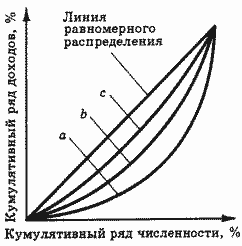
Рис. 5. Распределение населения по доходам с учетом налоговой и социальной политики. а — уровень доходов до уплаты налогов; b — уровень доходов после уплаты налогов; с — уровень доходов после осуществления мер социальной политики.
[8] Необходимо учитывать, что расчеты данным способом связаны с определенными погрешностями и неточностями, которые следует принимать во внимание при экономической интерпретации результатов.
Дата добавления: 2015-12-29; просмотров: 1191;
