От Ирвинга Фишера до Александра Конюса
В предыдущем разделе мы познакомились с индексами. Мы увидели, что в практике индексного исчисления приходится вводить некоторые допущения, не соответствующие логике теории.
Историческое развитие науки об индексах складывалось в борьбе разных позиций по поводу оправданности подобных допущений с точки зрения практического применения индексов.
Это вполне естественно, потому что индексы родились и совершенствовались в первую очередь как инструмент прикладного анализа. Между тем далеко не сразу практическая ценность индексов была признана широкими статистическими и экономическими кругами. Дело в том, что индекс можно исчислить по разным формулам, а это приводит к различным результатам. Представим себе человека, который потреблял только хлеб и молоко в течение двух месяцев. Данные о потреблении отражены в табл. 1.
Таблица 1. Исходные данные для примера о хлебе и молоке
| Продукт | Цена, руб./ед. | Объем, ед. | ||
| январь | февраль | январь | февраль | |
| p0 | p1 | q0 | q0 | |
| Хлеб, кг Молоко, л | 1 2 | 2 6 | 10 8 | 15 6 |
Наш потребитель захотел узнать, как же изменился уровень цен в феврале по сравнению с январем, и сосчитал индекс цен, применив для этого формулу простой арифметической средней:
| a = (Sp1/0)/n, (9) |
где а - простая арифметическая средняя из индивидуальных индексов цен р - индивидуальный индекс цен i-го продукта n - число потребляемых продуктов.
Вышло, что цены выросли на 150 ;%:
a = (2/1 + 6/2)/2 = 2,5.
В то же самое время государственные органы статистики исчислили индекс цен за февраль по формуле простой гармонической средней:
| h = n/(S1/p1/0), (10) |
где h - простая средняя гармоническая из индивидуальных индексов цен, и объявили, что цены выросли на 140 %:
| h = 2/[1/(2/1) + 1/(6/2)] = 2,4 |
Естественно, потребитель решил, что чиновники вздумали его обманывать, занижая действительный индекс цен. Он возмутился и обратился за объяснениями к статистикам.
Однако в начале XX в. статистики не смогли бы помочь возмущенному потребителю.
Дело доходило до того, что, например, голландский экономист H. Персоне в 1896 г. сделал следующее резюме: "Единственно возможным выводом... должно быть решение оставить навсегда всякие попытки вычислить и изобразить среднее движение цен при помощи индексов или чего-либо сходного".
Но... от индексного аппарата не отказались. Сегодня в экономической практике используется несколько десятков различных индексов.
Формулы, из-за употребления которых возник спор у нашего потребителя и его оппонентов, действительно используются для исчисления индексов относительно редко.
Формулы (9) и (10) относятся к категории простых, или невзвешенных. Они предполагают слишком грубое допущение: оба продукта считаются равнозначными для потребителя. Никак не учитывается тот факт, что хлеба и молока потребляется разное количество, а значит, изменение цен на эти продукты должно по-разному влиять на рассчитываемое значение индекса.
Для устранения этого недостатка статистиками были предложены так называемые агрегатные индексы. Рассмотрим явление, уровень которого характеризуется набором чисел (x1, x2, ..., xn) — примером могут служить цены различных товаров. Оценивая их совместное изменение, следует учесть значимость каждого индивидуального показателя, для этой цели используется набор так называемых весов (f1, f2, ..., fn). Агрегатный индекс представляет собой отношение:
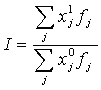 . .
|
Но в качестве весов берутся показатели реальных процессов, принимающие различные значения для базисного и отчетного периодов. Поэтому формула агрегатного индекса как бы раздваивается:
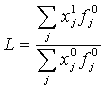 , (11) , (11)
|
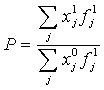 . (12) . (12)
|
В формуле (11) взвешивание выполняется по базисным значениям Индексы такого вида получили название индексов Ласпейреса[1]. В формуле (12) в роли весов выступают текущие значения такие индексы называются индексами Пааше [2]. С этими названиями связаны использованные нами обозначения индексов L и Р.
Стоит отметить, что веса совсем не обязательно должны быть физическими объемами и измеряться в тоннах, кубометрах и т. д. При исчислении индекса объемов в качестве весов могут выступать цены соответствующих продуктов.
В предыдущем разделе мы познакомились с индексами реального дохода и цен. Первый из них (7) - индекс Ласпейреса, в качестве весов использованы базисные цены; второй (8) - индекс Пааше, и здесь веса - это текущие объемы.
А сколько вообще индексов можно придумать? Какие их типы существуют? Есть ли основания, чтобы принимать одни и отвергать другие формулы?
Эти вопросы очень остро обсуждались в 20-е гг. нашего века. В то время были заложены основы современных представлений о том, что такое индексы. В 1922 г. американский статистик Ирвинг Фишер опубликовал работу, которая называлась “Построение индексов.
Учение об их разновидностях, тестах и достоверности”. Анализ проблемы индексов, проведенный автором, был настолько глубок, что практически все послефишеровские исследования в этой области так или иначе опираются на него.
Идея Фишера достаточно проста. Ясно, что в общем случае цены отдельных товаров за один период времени изменяются по-разному. Фишер заметил, что точки, соответствующие этим показателям (частным индексам цен), окажутся разбросанными, подобно осколкам разорвавшейся гранаты. Как у гранаты существует центр тяжести, относительно которого рассеиваются ее осколки, так и здесь есть явно выраженный сгусток точек, отражающий среднее движение цен.
Такой сгусток обязательно существует, потому что цены на отдельные продукты не являются независимыми величинами. Иногда эту взаимосвязь проследить легко, например между ценами на взаимозаменяемые или взаимодополняемые товары, иногда ее можно “увидеть” только с помощью специальных статистических методов. Продолжая аналогию с физикой, можно заметить, что для описания этого движения удобнее пользоваться именно средним показателем, вместо того чтобы иметь дело с изменением цен каждого отдельного товара.
Для понимания фишеровской концепции очень важно, что автор формировал ее с целью нахождения способа "легкого и быстрого исчисления индексов", а одним из неформальных требований к индексной формуле Фишер считал следующее: индекс должен быть “прост и понятен для непосвященных”.
Итак, индекс - это некоторая средняя из индивидуальных индексов цен. Но любой математик может предложить неограниченное количество формул, применяемых для нахождения среднего. Какую же из них выбрать?
Фишер применил простой исходный принцип, который оказался очень эффективным. В соответствии с ним достаточно сложное явление, такое как, например, движение уровня цен, может изучаться при помощи другого, которое подобно данному, но значительно проще его. Таким простым явлением в данном случае стало движение индивидуальных цен товаров.
Существует масса условий, которые с очевидностью выполняются для любого частного индекса. Фишер выбрал два из них в качестве формальных критериев (тестов) определения "идеальности" индексной формулы. Для нее тесты должны были выполняться без систематической ошибки.
Первый критерий Фишер назвал тестом обратимости во времени, или обратимости ситуаций. Его суть заключается в том, что произведение прямого индекса цен на обратный ему должно равняться единице. Математически это выражается следующей формулой:
| I1/0I0/1 = 1, (13) |
где I1/0 — прямой индекс цен I0/1 — обратный ему индекс цен, в котором исследуемый и базовый периоды (ситуации) меняются местами.
Для индивидуальных индексов равенство (13), естественно, выполняется. Например, если яблоки в Москве в два раза дороже, чем в Самаре, и, следовательно, в Самаре в два раза дешевле, чем в Москве, то произведение этих двух индексов будет равно единице:
(pM/pC)(pC/pM)(2/1)(1/2) = 1,
где pM — цена на яблоки в Москве рC — цена на яблоки в Самаре.
Второй критерий назывался тестом обратимости факторов и сводился к следующему утверждению: индекс стоимости равен произведению индекса объема на индекс цен:
| IvIq = Ip, |
где Iv - индекс стоимости Iq - индекс объема Ip - индекс цен.
Например, любой покупатель прекрасно понимает, что если он купил яблок в два раза больше, чем месяц назад, но по вдвое меньшей цене, то количество потраченных им денег не изменилось:
(q1/q0)(p1/p0) = (2/1)(1/2) = 1 = (v1/v0),
где q1, p1, v1 - соответственно количество, цена яблок и потраченные для их покупки деньги в текущем периоде; q0, p0, v0 - то же в базовом периоде.
Фишер применил эти критерии к 134 индексным формулам, многие из которых он вывел впервые. Огромнейшая вычислительная работа (вспомним, что в те времена не было калькуляторов) была проделана на основе массива данных о ценах и объемах на рынках США по 36 товарным позициям за шесть предвоенных и послевоенных лет.
Совершенной формулы Фишер не нашел: не было ни одной средней, одновременно отвечающей предложенным тестам. Впрочем, это только подтвердило его первоначальное предположение о том, что идеальной формулы среднего индекса не существует. Лучшей же оказалась формула, представляющая собой комбинацию индексов Ласпейреса и Пааше. Она получила название идеального индекса Фишера:
| ___ | ||
| F = | √ | LP |
Таблица 2. Расчетные формулы и результаты вычислений по тестам Фишера для примера о хлебе и молоке
| Индекс | Индексные формулы | Абсолютная ошибка в текстах | |||||
| прямой индекс цен (I1/0p) | обратный индекс цен (I0/1p) | индекс объема (I1/0q) | индекс стоимости (I1/0v) | ||||
| Ласпейерса, L | (Sp1q0)/(Sp0q0) | (Sp0q1)/(Sp1q1) | (Sq1p0)/(Sq0p0) | } | (Sq1p1)/(Sq0p0) | + 0,0699 | + 0,1660 |
| Пааше, P | (Sp1q1)/(Sp0q1) | (Sp0q0)/(Sp1q0) | (Sq1p1)/(Sq0p1) | - 0,0654 | - 0,1775 | ||
| Фишера, F | ЦL1/0pP1/0p | ЦL1/0pP1/0p | ЦL1/0pP1/0p |
Индекс Фишера удовлетворяет и тесту обратимости во времени, и тесту обратимости факторов. Мы можем проиллюстрировать эти свойства индекса Фишера на примере нашего потребителя, покупающего в январе и феврале только хлеб и молоко. В табл. 2 показаны расчетные формулы и результаты испытаний по фишеровским тестам для формул Ласпейреса, Пааше и Фишера в условиях этого примера. Расчеты же самого Фишера показали, что имеется около десятка индексных формул, дающих приблизительно одинаковые отклонения от тестов. В результате он сформулировал следующее утверждение: “Практические цели, поставленные перед индексом, не должны играть никакой роли при выборе формулы, по которой будет исчисляться данный индекс”.
Другими словами, если массив исходной информации сформирован, то можно применять любую из достаточно хороших по фишеровской классификации формул.
В чем же тогда кроется главная причина получения странных результатов при расчете по разным формулам? Фишер утверждал, что основные ошибки накапливаются на этапе группировки товаров в агрегированные группы.
Надо отметить, что при ограниченной номенклатуре товарного набора и небольшом периоде сравнения искажения результата несущественны. Другое дело, когда товаров настолько много, что включить их все в расчетную формулу невозможно (это обычная ситуация для любого потребительского набора). Приходится использовать некоторые наиболее типичные товары-представители, например, из всех сортов яблок - один.
Формализованных методов подобного отбора не существует. В результате проблема построения “хорошего” индекса смещается в сферу во многом интуитивных оценок: сколько и каких товаров оставить в наборе, чтобы, с одной стороны, не исказить результат, а с другой - обеспечить практическую выполнимость задачи получения исходной информации о ценах и объемах.
Экономическая практика в принципе подтвердила основные выводы Ирвинга Фишера.
Например, отсутствие удовлетворительных экономических аргументов в пользу того или иного индекса не мешает для измерения движения цен в нашей стране свыше 70 лет применять индекс Пааше, а в США - Ласпейреса.
Между тем в начале 20-х гг. работа Фишера вызвала бурю как хвалебных высказываний, так и критики. Впрочем, автор был готов к такому повороту событий, написав во вступительной статье: “Результаты иногда покажутся не совсем надежными, так как одни из них - выводы из наблюденного, а другие получены эмпирически (а эти области не всегда сочетаются)”.
Главным пафосом оппонентов Фишера был тезис о том, что его индексы не имеют четкого экономического смысла, а сам подход никак не сочетается с экономическими теориями, господствовавшими в то время. На волне подобных критических замечаний (не отвергавших, впрочем, огромную ценность работы) родился новый подход к исчислению индексов. Его впервые обосновал и сформулировал сотрудник московского Конъюнктурного института Александр Александрович Конюс в своей статье “Проблема истинного индекса стоимости жизни”. Конюс попытался ликвидировать “экономический пробел” в теории Фишера. Для этого он привлек концепции уровня и стоимости жизни.
Уровень жизни данной семьи - это состояние удовлетворения потребностей, определяемое потреблением тех или иных благ, т.е. то, что мы называем уровнем полезности потребительского набора. Уровень жизни, - чисто качественная характеристика. Понятно, что одно и то же состояние удовлетворения потребностей может достигаться при различных комбинациях цен за счет изменения общего расхода потребителя.
Однако для построения индекса нужен какой-то измеримый количественный показатель. У Конюса - это стоимость жизни, денежная стоимость благ, которые потребляются в течение некоторого промежутка времени.
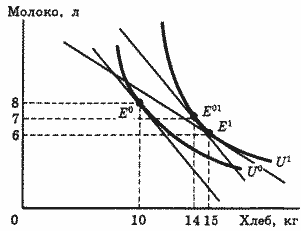
Рис. 4. Геометрическая иллюстрация к построению индекса Конюса
На основе такой экономической начинки Конюс предложил отличную от фишеровской форму индекса цен (или стоимости жизни). Индекс стоимости жизни - частное от деления стоимости жизни в одном промежутке времени на стоимость жизни в другом промежутке времени, если в течение обоих промежутков уровень жизни был одинаковым (рис. 4):
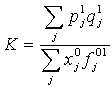 , ,
|
где q1j - количество благ, фактически потребленных в текущем периоде, p0j, p1j - цены в базисном и текущем периодах; q01j - количество благ, которые выбрал бы рациональный потребитель, если бы цены изменились до текущего уровня , чтобы сохранить базисный уровень жизни.
Таким образом, индекс Конюса показывает, как изменилась денежная стоимость благ, необходимых для поддержания определенного уровня полезности потребительского набора. При этом состав набора может быть различным в исследуемые периоды, что соответствует экономической действительности.
Стоит отметить, что экономической действительности совсем не соответствует одно следствие из теории Конюса, а именно: состояние предпочтений потребителя (карта безразличия) стабильно во времени. Конюсу оставалось надеяться, что при достаточно малых промежутках времени данный постулат будет более или менее реальным.
Обратимся опять к примеру о потребителе, покупающем только хлеб и молоко (рис. 4). Изменение ценовых пропорций и бюджетных ограничений, приводит к тому, что в феврале стал потребляться не набор Е0 (10 кг хлеба + 8 л молока), а набор Е1 (15 кг хлеба + 6 л молока).
При этом общая полезность набора повысилась до уровня U1.
Для построения индекса нам необходимо знать, сколько хлеба и молока покупал бы наш потребитель, чтобы сохранить этот уровень жизни при обратном изменении цен (до 1 руб./кг и 2 руб./л соответственно). На бумаге все выглядит очень просто. При верности гипотезы о рациональном поведении потребителя этой совокупностью будет набор из 14 кг хлеба и 7 л молока. На практике же Конюс столкнулся с серьезнейшими трудностями.
Ведь в действительности набор гипотетический, его нельзя увидеть ни в какой статистической отчетности. А можно ли в принципе его определить?
Теоретически - да. Для этого необходимо вывести уравнение кривой безразличия в текущем периоде (кривая U1 на рис. 4), т. е. нарисовать то, что считается известным при графическом способе.
Математически такая задача решается составлением такого количества бюджетных уравнений для данного потребителя, которое равно квадрату числа исследуемых продуктов. Для нашего примера достаточно четырех уравнений. В общем же случае надо провести n бюджетных исследований в n периодах времени, где n - число продуктов.[3]
Для индивидуального потребителя проводить такую работу бессмысленно. Его предпочтения меняются слишком быстро, да и практическая ценность результата невелика. Задачу можно пытаться решать для группы потребителей, считая, что их “усредненные” предпочтения - гораздо более устойчивая характеристика во времени и по отношению к изменению ценовых пропорций.
Зная угол наклона гипотетической бюджетной линии, соответствующей набору Е01 (см. формулу (2)), а также то, что она является касательной к найденной кривой безразличия, без труда определяется набор Е01.
Сотрудники Конъюнктурного института, конечно, проводили бюджетные исследования.
Существовали даже специальные агенты, которые ежедневно ходили на московские рынки и участвовали в торгах с продавцами, чтобы определить реальную цену в момент совершения покупки.
Однако вспомним, что n - это число позиции в потребительском наборе, которых вряд ли может быть менее 30—40. Добыть такое количество исходной информации было невозможно, тем более в Советской России, статистическое хозяйство которой было в плачевном состоянии. В результате индекс Конюса так и остался чисто теоретической конструкцией. Собственно говоря, воплотить его идеи в практическую экономику не удалось никому, хотя такие попытки были.
Имена Ирвинга Фишера и Александра Конюса очень важны для истории индексной науки. С ними связывают два больших направления в теории индексов. Фишеровские индексы называют статистическими, а индексы, основанные на идеях Конюса, - экономическими, или функциональными.
Эти названия достаточно точно отражают идеологию каждого из направлений.
С точки зрения теории отдать предпочтение ни одному из этих подходов нельзя. Практика же исчисления индексов показывает явный перевес статистического подхода.
Этот результат вполне закономерен, если вспомнить слова Фишера о своей книге: “Этот труд - комбинация практического и теоретического анализа, но теоретическая часть целиком подчинена практической”. Остается добавить, что “любой индекс - только модель, которая с разной степенью приближения отражает реальное состояние дел”. С этим выводом А. Конюса следует согласиться.
Дата добавления: 2015-12-29; просмотров: 716;
