Стабильность равновесия

РАЗДЕЛ 1. Понятие устойчивости равновесия. Паутинообразная модель

В лекции 1, раздел 2, мы обсуждали проблемы существования и единственности равновесия. Однако является ли само по себе существование равновесия гарантией того, что система действительно достигает равновесного состояния? Воспользуемся весьма простым примером. Очевидно, что шарик, лежащий на дне лунки, находится в состоянии равновесия. Однако, если постараться, можно установить этот же шарик и на макушке сферы. Таким образом, и в том и в другом случае равновесие существует. Но если в первом случае физические силы естественным образом двигают шарик к положению равновесия, то во втором равновесие нашего шарика носит весьма шаткий характер - малейшее колебание неизбежно заставит его скатиться вниз.

Обратимся теперь к рыночному равновесию (рис. 1).

Представим себе, что в силу каких-либо причин цена отклонилась от первоначального равновесного значения Р' (например, цены P₁ и P₂). Зададимся следующим вопросом: вернется ли рынок с течением времени к первоначальному состоянию равновесия в точке Е и примет ли цена первоначальное равновесное значение Р', или этого не произойдет?

Эта проблема носит название проблемы устойчивости (стабильности) равновесия.

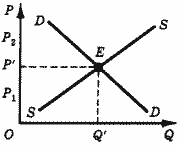
Рис. 1.Равновесие на рынке.

Интерес экономической теории к проблеме устойчивости равновесия легко объясним.

Ведь выводы об устойчивости (неустойчивости) рыночного равновесия могут привести в свою очередь к важным выводам о ненужности (или, напротив, необходимости) государственного вмешательства в экономику. В самом деле, не стоит всерьез беспокоиться о судьбе шарика, брошенного в лунку, - рано или поздно он займет свое место. Но если только мы хотим удержать в равновесии шарик, лежащий на макушке сферы, то нередкими будут ситуации, когда придется придерживать этот шарик руками.

Очевидно, что анализ экономического равновесия с точки зрения его устойчивости требует от нас определения динамики изменения цены во времени (рис. 2, 3); иными словами, фактор времени должен быть включен в анализ явным образом. На рис. 2 цена возвращается к первоначальному равновесному значению. Такое равновесие является устойчивым. На рис. 3 цена стремится к первоначальному значению, никогда не достигая его. Такое равновесие называется асимптотически или условно устойчивым равновесием.

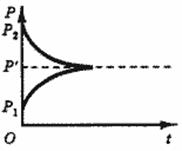
Рис. 2. Устойчивое равновесие.

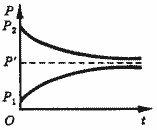
Рис. 3. Асимптотически устойчивое равновесие.

Динамика изменения цены может характеризоваться также циклическими колебаниями различного вида (рис. 4-6).

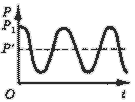
Рис. 4.Рис. 4. Равномерные колебания.

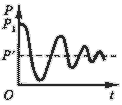
Рис. 5. Затухающие колебания.

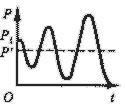
Рис. 6. Взрывные колебания.

Равновесие может быть устойчивым для всех возможных значений цены (глобальная устойчивость - рис. 7) или только для значений цены в некоторой окрестности Р' (локальная устойчивость - рис. 8).

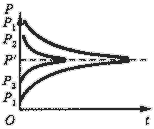
Рис. 7. Глобальная устойчивость.

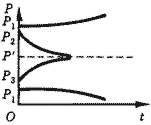
Рис. 8. Локальная устойчивость.

Заметим, что до сих пор мы рассматривали устойчивость как способность цены после некоторого возмущения вернуться к первоначальному значению равновесия Р'. Однако если это возвращение не происходит, то возможны различные случаи: цена неограниченно возрастает или падает (рис. 9), или принимает новое равновесное значение, отличное от Р' (рис. 10).

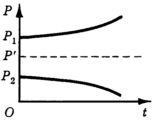
Рис. 9. Цена неограниченно возрастает или падает.

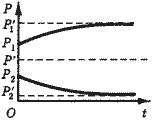
Рис. 10. Цена принимает новое равновесное значение.

В этом смысле также говорят иногда об устойчивости равновесия как о способности системы достигнуть состояния равновесия в точке, отличной от первоначального равновесного положения.

В экономике, говоря об устойчивости, чаще всего имеют в виду устойчивость первоначального равновесного значения, однако пользоваться термином "устойчивость" следует все же весьма осторожно, так как его конкретный смысл часто обусловлен особенностями рассматриваемой модели.

Перейдем теперь непосредственно к анализу устойчивости рыночного равновесия. Как мы уже знаем, такой анализ требует построения модели, в которой фактор времени был бы учтен явным образом (динамическая модель рынка). Рассмотрим в качестве примера одну из простейших динамических моделей, так называемую паутинообразную модель.

Представим себе производителей пшеницы, картофеля или какой-либо иной сельскохозяйственной культуры. Очевидно, что, принимая во время сева решения об объеме производства продукции, они не могут знать цены на эту продукцию в период ее реализации после сбора урожая. В этом случае решения об объеме производства могут основываться только на ожидаемых производителями будущих ценах на их продукцию.

Предположим теперь, что производители ожидают в будущем периоде сохранения фактически установившихся в настоящем периоде цен. Тогда объем рыночного предложения товара в каждом периоде зависит от цены этого товара в предыдущем периоде:

где Q^S_t - объем предложения товара в период t; P_t-1 - фактическая цена товара в период t-1.

Такой подход применим, разумеется, не только к сельскому хозяйству, но и к любой отрасли с фиксированным циклом производства. Даже предложение такого специфического товара, как инженеры, зависит, наверное, от заработной платы инженера пять лет назад, когда нынешние выпускники были абитуриентами. Оговоримся сразу, что наша модель поведения производителей (как и любая модель) является некоторым упрощением действительности. Так, мы предполагаем, что производитель, приняв решение об определенном объеме предложения, уже не сможет скорректировать это решение, даже если фактическая цена товара окажется, например, ниже ожидаемой (хотя на самом деле пшеницу можно оставить на поле неубранной, а студент может бросить институт). Мы не предполагаем также возможности образования запасов и их последующей реализации и, уж конечно, не учитываем таких случайных явлений, как естественные колебания урожайности. Однако даже при всех этих допущениях наша гипотеза о поведении производителей, не знающих заранее цены выпускаемого ими товара, представляется довольно правдоподобной, так что интересно посмотреть, к каким выводам относительно устойчивости равновесия приводит основанная на этой гипотезе динамическая модель. Попробуем решить эту проблему графически (рис. 11).

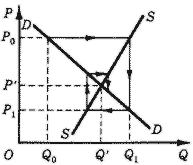
Рис. 11. Паутинообразиая модель.

На рис. 11 линия SS характеризует зависимость объема предложения товара от фактической цены этого товара в предыдущем, периоде. Линия DD характеризует зависимость объема спроса на товар от цены товара в данном, периоде (ведь потребителям нет нужды определять объем закупок заранее, не имея точной информации о ценах):

где Q^D_t- объем спроса на товар в период t; P - цена товара в период t.

Пусть цена в некоторый начальный период t = 0 была равна P₀ , по ней было куплено Q₀ единиц товара. Тогда в следующем периоде t = 1 производители выбросят на рынок Q₁ единиц товара. Этот объем предложения будет в свою очередь реализован по цене P₁ и т. д. (дальнейшее движение не составит труда для читателя). На рис. 11 показано, что система стремится к положению равновесия в точке с координатами (P', Q'), т. е. равновесие является устойчивым. Однако всегда ли дело будет обстоять именно так?

Заметим, что на рис. 11 линия предложения (SS) круче линии спроса (DD). Рассмотрим теперь случаи, когда линия спроса круче линии предложения (рис. 12) и когда углы наклона линий спроса и предложения равны (рис. 13).

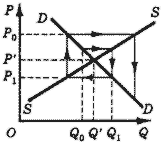
Рис. 12. Неустойчивое равновесие.

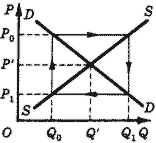
Рис. 13. Регулярные колебания вокруг положения равновесия.

Сформулируем следующие выводы из графического анализа (эти выводы могут быть строго доказаны с помощью математического аппарата разностных уравнений):

1) равновесие является устойчивым, если угол наклона кривой предложения круче угла наклона кривой спроса;

2) равновесие является неустойчивым, с взрывными колебаниями цены, если угол наклона кривой спроса круче угла наклона кривой предложения;

3) цена совершает регулярные колебания вокруг положения равновесия, если углы наклона кривых спроса и предложения равны.

Представим графически динамику изменения цены во времени во всех трех перечисленных случаях (рис. 14-16).

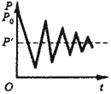
Рис. 14. Затухающие колебания.

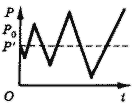
Рис. 15. Взрывные колебания.

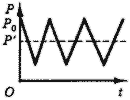
Рис. 16. Регулярные колебания.

Таким образом, теоретически паутинообразная модель предполагает возможность неустойчивости рыночного равновесия. Однако насколько реальна такая возможность на практике? Ведь увидев, что их ожидания постоянно не реализуются, производители наверняка постараются усовершенствовать механизм формирования этих ожиданий. В самом деле, зная динамику изменения цены за несколько предшествующих периодов, можно получить гораздо более точное представление о будущих ценах, чем если просто распространять фактическую цену данного периода на следующий период. Другим стабилизирующим равновесие фактором может послужить образование запасов товаpa и изменение этих запасов (увеличение запасов в одни периоды и уменьшение - в другие).

Дальнейший анализ приводит нас к построению весьма сложных моделей, рассмотрение которых невозможно в рамках настоящего издания.

Однако даже простейшая паутинообразная модель является хорошей иллюстрацией динамического подхода к проблеме устойчивости рыночного равновесия, позволяя понять некоторые особенности этого подхода.

РАЗДЕЛ 2. Сравнение подходов Вальраса и Маршалла к проблеме устойчивости равновесия

Анализ рыночного равновесия с точки зрения его устойчивости требует от нас определенного представления о том механизме, посредством которого устанавливается равновесие на рынке. По-разному понимали действие этого механизма два крупнейших экономиста XIX в. - Л. Вальрас и А. Маршалл.

Проследим вначале за аргументацией Вальраса.

Каким образом система достигает положения равновесия?

Допустим, первоначальное значение цены - P₁ (рис. 17).

По этой цене производители готовы продать Q₁ единиц товара, а потребители хотят купить Q₂ > Q₁ единиц товара.

Возникает избыточный спрос ВС = Q₂ - Q₁.

Рис. 17. Устойчивость равновесия по Вальрасу.

Потребители начинают конкурировать между собой за обладание товаром, и вследствие этого цена повышается. Процесс (который Вальрас называл процессом "нащупывания" равновесной цены) идет непрерывно до тех пор, пока избыточный спрос не становится равным нулю в точке -Е. Аналогично, если первоначальное значение цены - Р₂, возникает избыточное предложение AL;конкуренция среди продавцов понижает цену, пока избыточное предложение не становится равно нулю в точке Е.

Таким образом, в точке Е на рынке устанавливается равновесие, так как здесь нет ни избыточного спроса, ни избыточного предложения и нет стимулов к изменению цены.

По-иному объяснял механизм установления равновесия Маршалл (рис. 18).

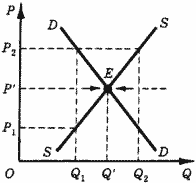
Рис. 18. Устойчивость равновесия по Маршаллу.

Он предположил, что продавцы реагируют на разность цены спроса и цены предложения.

Так, при объеме предложения Q₁ цена спроса P₂ больше цены предложения P₁, и продавцы будут увеличивать объем предложения до достижения точки Е. Если цена спроса меньше цены предложения, предложение будет, наоборот, сокращаться, пока рынок не окажется в состоянии равновесия в точке Е.

Таким образом, в случае, когда кривая спроса имеет отрицательный, а кривая предложения - положительный наклон, модели Вальраса и Маршалла приводят к одному и тому же устойчивому положению равновесия. Однако всегда ли кривые спроса и предложения имеют такой вид? Вспомним рис. 6,а из лекции 1, раздел 2, где изображена так называемая загибающаяся кривая предложения труда. В верхней своей части эта кривая имеет отрицательный наклон. Отрицательным наклоном могут характеризоваться также кривые предложения на валютном рынке. Рассмотрим теперь рынок с отрицательно наклоненной кривой предложения, чтобы посмотреть, к одинаковым ли выводам относительно условий устойчивости равновесия приведут нас модели Вальраса и Маршалла в этом случае.

Рассмотрим сначала случай, когда кривая предложения направлена вниз и угол наклона кривой предложения круче угла наклона кривой спроса. Воспользуемся сначала аргументацией Вальраса (рис. 19, а). Пусть первоначальная цена Р₀. При этой цене образуется избыточный спрос Q₁Q₂ и цена повышается до точки Е. Равновесие устойчиво.

Применим теперь подход Маршалла (рис. 19, б). Пусть первоначальное предложение равна Q₀. Цена спроса превышает цену предложения (P₂ > P₁), предложение увеличивается, и цена спроса ещё более превышает цену предложения. Движение происходит в направлении, противоположном положению равновесия. Равновесие неустойчиво.

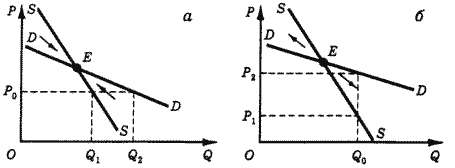
Рис. 19. Равновесие, устойчивое по Вальрасу (а), но неустойчивое по Маршаллу (б).

Пусть теперь кривая предложения снова направлена вниз, но угол ее наклона к оси Р менее крут, чем угол наклона кривой спроса (рис. 20). Читатель без труда убедится, что равновесие устойчиво по Маршаллу и неустойчиво по Вальрасу.

Рис. 20. Равновесие, неустойчивое по Вальрасу (а), но устойчивое по Маршаллу (б).

Таким образом, модели Вальраса и Маршалла приводят, хотя бы с теоретической точки зрения, к различным условиям устойчивости равновесия. Причиной этих различий являются различные исходные представления о функционировании рыночного механизма, лежащие в основе рассматриваемых нами моделей.

Можно ли сказать, что модель Вальраса правильно описывает действие рыночного механизма, а модель Маршалла - неправильно (или наоборот)? Наверное, нет. В самом деле, процесс установления равновесия в коротком периоде лучше описывается с помощью модели Вальраса, когда, например, избыточный спрос ведет к повышению цены до равновесного значения.

В то же время для анализа достижения равновесия в длительном периоде удобнее пользоваться моделью Маршалла, в которой объем предложения возрастает, если цена спроса превышает цену предложения.

Отметим, что модели Вальраса и Маршалла имеют одно общее свойство, которое отличает их от рассмотренной в разделе 1 настоящей лекции паутинообразной модели.

Вспомним, как вводился фактор времени в паутинообразную модель. Время было разбито на интервалы одинаковой продолжительности, причем в течение каждого интервала переменные модели оставались постоянными. Цена в паутинообразной модели изменялась скачками от предыдущего периода к последующему. По-другому обстоит дело в моделях Вальраса и Маршалла.

Здесь время является непрерывно изменяющейся переменной, непрерывно изменяется и цена. В паутинообразной модели объем предложения в данном периоде обусловливается ценой продукции в предыдущем периоде. Это обстоятельство вызывает в свою очередь теоретическую возможность неустойчивости равновесия даже при "нормальном" виде кривых спроса и предложения (кривая предложения имеет положительный, а кривая спроса - отрицательный наклон). В моделях Вальраса и Маршалла такая возможность исключена.

Наш вывод состоит в том, что для анализа устойчивости рыночного равновесия могут применяться различные динамические модели (в зависимости от особенностей конкретного рынка и целей исследования), причем эти модели приводят к различным условиям устойчивости.