Заменяемость и дополняемость
РАЗДЕЛ 1. Кривая безразличия и норма замены
Сейчас мы приступаем к более подробному рассмотрению фундаментальных для экономического знания представлений о заменяемости и дополняемости. Для этого читателю необходимо познакомиться с рядом новых понятий.
Как, вероятно, помнит читатель (лекция 2), взаимосвязь между спросом на товар и его ценой определяется полезностью товара с позиции потребителя. В лекции 2 полезность каждого товара рассматривалась изолированно - полезность зависела лишь от количества приобретаемых единиц данного товара. Очевидно, однако, что в реальной действительности спрос потребителя на некоторый товар зависит от намерений по закупке других товаров не только с точки зрения ограниченного бюджета (чем больше средств тратится на яблоки, тем меньше остается на книги), но и с точки зрения полезности (чем больше покупается яблок, тем меньше нужно груш). Иными словами, потребитель сталкивается с необходимостью выбора оптимального набора или комбинации нескольких (а в более широком смысле - всех) приобретаемых им товаров, причем сокращение потребления одного товара может быть заменено (компенсировано) увеличением потребления другого товара без снижения общей полезности данного товарного набора.
Проблема выбора оптимального набора товаров привела в экономической науке к возникновению техники, так называемых кривых безразличия, которая и будет проиллюстрирована в настоящем разделе на примере двух товаров.
Представим себе, что потребителю нужно выбрать некоторую комбинацию двух товаров.
Очевидно, любой акт выбора имеет две стороны: желания (которые определяются вкусами и предпочтениями) и возможности (доступность товаров для потребителя).
Для анализа потребительских предпочтений как раз и служат кривые безразличия.
Поясним это на примере. Пусть некто решает приобрести 10 яблок и 20 конфет.
Попробуем определить, какие другие наборы (комбинации) яблок и конфет имеют, с точки зрения потребителя, общую полезность, равную полезности этого первоначального набора. Иначе говоря, потребителю безразлично, какой из этих наборов выбрать (причем безразлично с точки зрения вкуса, а не цен). Представим полученные данные в табл. 1.
Таблица 1. Наборы яблок и конфет, имеющие для потребителя равную суммарную полезность
| Набор | Яблоки | Конфеты |
| А | ||
| В | ||
| С | ||
| D | ||
| Е | ||
| F |
Представим теперь информацию табл. 1 графически. Будем откладывать по вертикальной оси количество яблок, а по горизонтальной - количество конфет с тем, чтобы каждому наборуэтих двух товаров соответствовала бы точка в графическом "пространстве товаров".
Отметим теперь на графике точки, соответствующие наборам А-F из табл. 1.
На рис. 1 эти точки соединены плавной линией ii. Разумно предположить, что все точки, лежащие на этой линии, характеризуют комбинации товаров, имеющие для потребителя равную общую полезность (т. е. потребителю безразлично, какую из этих комбинаций выбрать). Поэтому линия ii называется кривой безразличия.
Рассмотрим любую комбинацию товаров, лежащую выше кривой ii (например, комбинацию К - 20 яблок и 20 конфет).
Доставит ли эта комбинация потребителю большее удовлетворение, чем комбинации, лежащие на кривой безразличия (например, комбинация А)? Рассмотрим количество яблок и конфет в обоих наборах:
Комбинация А Комбинация К
30 яблок 20 яблок
б конфет 20 конфет
Вопрос остался открытым, так как неизвестно, что в этом случае предпочтительнее для потребителя: 10 лишних яблок или 15 лишних конфет. Однако мы знаем другое: общая полезность набора А равняется общей полезности набора С (13 яблок и 15 конфет).
Сравним тогда комбинацию К с комбинацией С:
Комбинация С Комбинация К
13 яблок 20 яблок
15 конфет 20 конфет
Очевидно, что комбинация К будет иметь для потребителя полезность большую, чем полезность комбинации С, а следовательно, и комбинации А и всех других комбинаций, лежащих на кривой безразличия ii.
Из приведенных выше рассуждений можно с уверенностью заключить, что любая точка, лежащая выше кривой безразличия ii, будет более предпочтительной для потребителя, чем точки кривой безразличия. С другой стороны, любая точка, лежащая ниже кривой безразличия ii (например, точка Н на рис. 1), дает потребителю меньшее удовлетворение, чем точки кривой безразличия.
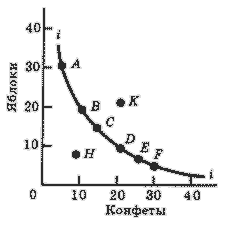
Рис. 1. Кривая безразличия.
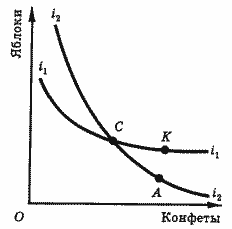
Рис. 2. Пересечение кривых безразличия: такого быть не может!
Сформулируем теперь некоторые общие свойства кривых безразличия.
1.Через любую точку в графическом пространстве товаров (рис. 1) может быть проведена соответствующая кривая безразличия, т. е. для любой комбинации товаров (яблок и конфет) могут быть найдены другие комбинации, имеющие для потребителя такую же общую полезность.
Это свойство основывается на простом предположении о том, что потребитель может сравнивать с помощью отношений предпочтения или безразличия все возможные наборы товаров.
2.Две кривые безразличия не могут пересекаться.
Рассмотрим рис. 2. Предположим, что кривые безразличия i1i1 и i2i2 пересекаются в точке С. Тогда потребитель безразличен в выборе между С и А и в выборе между С и А.
Следовательно, потребитель безразличен в выборе между К и А. Но точка А лежит ниже кривой i1i1 , поэтому, как нам уже известно, полезность комбинации А меньше полезности комбинации К. Очевидно, что пересечение кривых безразличия невозможно.
3. На основании свойств 1 и 2 может быть построена карта безразличия потребителя (рис. 3).
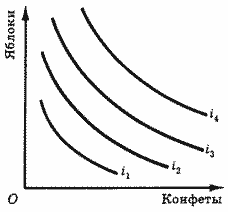
Рис. 3. Карта безразличия.
Комбинации товаров, лежащие на более высоких кривых безразличия, имеют для потребителя большую полезность (по правилу о точках, лежащих выше кривой безразличия).
4. Кривые безразличия имеют отрицательный наклон, так как уменьшение количества одного товара должно быть заменено (компенсировано) увеличением количества другого товара для сохранения общей полезности набора товаров.
5. Свойства 1-4 достаточно наглядны и не вызовут, вероятно, возражений читателя.
Однако они не объясняют в полной мере используемой нами формы кривых безразличия.
Действительно, эти свойства характеризуют, например, кривые, изображенные на рис. 4.
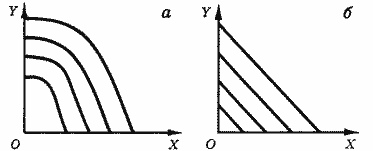
Рис. 4. Кривые безразличия.
Применяемые же нами кривые безразличия (рис. 1-3) имеют вполне определенную форму - все они являются выпуклыми по отношению к началу координат (наклон кривых безразличия уменьшается при движении вправо вдоль горизонтальной оси). Попробуем объяснить, с чем связано такое предположение. Рассмотрим еще раз пример с конфетами и яблоками (табл. 1).
Легко заметить, что при переходе от набора А к набору В, от набора В к набору С и т. д. потребитель всякий раз получает пять дополнительных конфет, но количество яблок, которое он при этом теряет, все время уменьшается от 12 (при переходе от А к В) до одного (при переходе от Е к F). В этом случае говорят об уменьшающейся предельной норме замены. Предельной нормой замены одного товара другим (яблок конфетами) называется количество яблок, которое потребитель согласен потерять с тем, чтобы получить одну дополнительную конфету (при одинаковой общей полезности комбинаций товаров).
Предельная норма замены = -ΔY / ΔX.
Таблица 2. Уменьшение предельной нормы замены
| Переход | Изменение количества яблок(ΔY) | Изменение количества конфет(ΔX) | Предельная норма замены |
| От набора А к набору В | -12 | +5 | 12 / 5 = 2.4 |
| От набора В к набору С | -5 | +5 | 5 / 5 = 1 |
| От набора С к набору D | -3 | +5 | 3 / 5 = 0.6 |
| От набора Л к набору Е | -1 | +5 | 2 / 5 = 0.4 |
| От набора Е к набору F | -1 | +5 | 1 / 5 =0.2 |
Как видно из табл. 2, предельная норма замены на кривой безразличия ii (рис. 5) уменьшается от 2.4 до 0.2. Это уменьшение легко объяснить логически. В точке А потребитель имеет относительно много яблок и относительно мало конфет. При движении от точки А вправо по кривой безразличия количество яблок уменьшается, а количество конфет увеличивается. Очевидно, чем больше конфет уже имеется у потребителя, тем меньшим количеством все более дефицитных яблок он готов пожертвовать, чтобы получить дополнительную конфету.
На рис. 5 легко увидеть (и доказать), что предельная норма замены графически характеризуется наклоном кривой безразличия. Таким образом, предположение об уменьшающейся предельной норме замены привело нас к пятому свойству кривых безразличия: наклон кривой безразличия уменьшается при движении вправо, кривые безразличия выпуклы по отношению к началу координат.
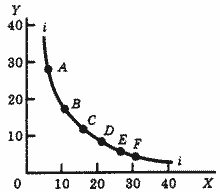
Рис. 5. Уменьшающаяся предельная норма замены.
Рассмотрим теперь два особых случая конфигурации кривых безразличия. Отметим прежде всего, что многие товары находятся друг с другом в отношениях взаимозаменяемости и взаимодополняемости с точки зрения потребителей.
Взаимозаменяемыми называют товары, которые служат для удовлетворения одинаковых или сходных потребностей, так что потребитель может выбрать какой-то один из этих товаров (сигареты различных марок). С другой стороны, товары, которые потребляются совместно (спички и сигареты), называются взаимодополняемыми. Представим кривые безразличия для двух крайних случаев: совершенной взаимозаменяемости (если потребителю все равно, какие сигареты купить) и жесткой взаимодополняемости (если спички используются только при курении).
В случае совершенной взаимозаменяемости два товара рассматриваются как один товар, и кривая безразличия вырождается в прямую линию (рис. 6), т. е. предельная норма замены становится постоянной величиной.
При жесткой взаимодополняемости (рис. 7) каждому уровню удовлетворения потребителя соответствует одна комбинация товаров.
Увеличение количества одного товара без увеличения количества другого не изменяет полезности этой комбинации для потребителя (предельная норма замены равна нулю).
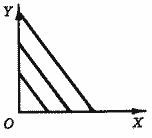
Рис. 6. Совершенная взаимозаменяемость.

Рис. 7. Жесткая взаимодополняемость.
Такие ситуации редки на практике. Большинство реальных кривых безразличия находятся между двумя крайними положениями, а многие товары являются взаимозаменяемыми и взаимодополняемыми в той или иной мере.
Так, все продукты питания в какой-то степени взаимозаменяемы, в то же время они могут быть взаимодополняемыми при приготовлении салатов, пирогов, подготовке праздничного ужина т. д. (и все это зависит от вкусов). Вообще поиск связей в отношении взаимодополняемости и взаимозаменяемости товаров - необыкновенно интересное и сложное занятие. Как связано между собой потребление пива и газет, билетов на концерт и садовых домиков, автомобилей и магнитофонных кассет? Пусть читатель сам ответит на эти вопросы или попробует придумать другие, более интересные цепочки товаров.
Дата добавления: 2015-12-29; просмотров: 939;
