Эластичность спроса и предложения. РАЗДЕЛ 1. Что показывает эластичность
РАЗДЕЛ 1. Что показывает эластичность
Функция спроса Q = D(P) устанавливает зависимость объема спроса Q от цены P. Главный вопрос, возникающий при анализе этой зависимости, - это вопрос о том, насколько резко изменится объем спроса при том или ином изменении цены.
Обычно степень влияния одной переменной на другую, зависимую от нее, измеряют производной соответствующей функции. Если ΔР - изменение цены, ΔQ - вызванное им изменение объема спроса, то значение производной покажет, на сколько единиц изменится спрос в расчете на единичное изменение цены в бесконечно малой окрестности исходного значения. Графически этому соответствует крутизна наклона касательной к кривой спроса по отношению к оси цен.
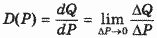 , (1) , (1)
|
Напомним читателю, что в экономической литературе принято откладывать объемы по горизонтальной оси, а цены - по вертикальной. Если в качестве аргумента рассматривается цена, а объем выступает в роли функции (как в настоящей лекции), читателю нужно иметь в виду, что оси аргумента и функции расположены непривычным образом.
Однако непосредственное использование производной как характеристики реакции спроса на изменение цен не дает ответа на ряд вопросов, интересующих экономиста. Пусть повышение цены за 1 кг картофеля на 10 коп. снижает годовой объем спроса на 10 кг, т. е. ΔР = 0.1 руб./кг, ΔQ = -10 кг/год (знак "минус" соответствует уменьшению). Считая эти изменения малыми, можно приближенно оценить производную:
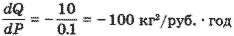 , ,
|
(обратите внимание на размерность!). Допустим, аналогичным образом мы установили, что для обуви:
 , ,
|
Какая из этих величин больше? Вопрос бессмыслен, и не только из-за того, что величины, измеренные в различных единицах, несопоставимы. Даже формальное совпадение единиц не разрешило бы трудности, так как 1 кг картофеля для потребителя не эквивалентен такому же количеству, скажем, чая.
Перечисленные (и иные) трудности можно преодолеть, если в качестве основного показателя реакции спроса на изменение цены использовать не производную, а эластичность спроса по цене - предел отношения относительного приращения объема δQ = ΔQ/Q к относительному приращению цены δР = ΔР / Р при условии, что последнее стремится к нулю:
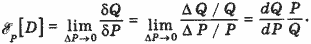 , (2) , (2)
|
При анализе относительных изменений эластичность играет примерно такую же роль, что производная - при анализе абсолютных изменений. Свойства этой характеристики зависимостей изложены в Математическом приложении (далее - МП), II.
Эластичность - безразмерная величина; ее использование снимает сложности, связанные с единицами и масштабами рассматриваемых величин. Эластичность и производная не связаны друг с другом однозначно, хотя и совпадают по знаку (поскольку Р и Q - положительные величины), и в одних и тех же случаях стремятся к нулю (когда реакция спроса на изменение цены отсутствует) или к бесконечности (когда потребитель "бесконечно сильно" реагирует на ничтожное изменение цены). Крутизна наклона кривой в общем случае не характеризует величину эластичности, ее геометрические свойства несколько менее наглядны.
В нормальных случаях с увеличением цены объем спроса уменьшается. Поэтому можно считать, что всегда Εp[D] < 0, и при анализе спроса знак эластичности не представляет интереса. Для измерения величины реакции спроса на изменение цены удобнее использовать абсолютную величину эластичности:
η = |Εp[D]|(3)
Некоторые авторы, чтобы иметь дело с положительными показателями, определяют эластичность потребления по спросу как:
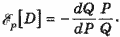 , (1) , (1)
|
Такое определение не соответствует общему определению эластичности функции.
Спрос называют неэластичным, если 0 < η < 1, и эластичным, если η > 1. Посмотрим, с какими реальными обстоятельствами связана эластичность спроса по цене (табл. 1; рис.1).
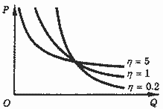
Рис. 1. Кривые спроса с низкой (=0.2), единичной (=1) и высокой (=5) эластичностью.
Таблица 1. Реакция покупателей на изменения цены
| η | Характер спроса | Поведение покупателей | |
| при снижении цены | при возрастании цены | ||
| η = ∞ | Совершенно эластичный | Повышают объем закупок на неограниченную величину | Снижают объем закупок на неограниченную величину (полностью отказываются от товара) |
| 1 < η < ∞ | Эластичный | Значительно повышают объем закупок (спрос растет более высоким темпом, чем снижается цена) | Значительно снижают объем закупок (спрос снижается более высоким темпом, чем растет цена) |
| η=1 | Единичная эластичность | Спрос растет в том же темпе, что и падает цена | Спрос снижается в том же темпе, что и растет цена |
| 0< η <1 | Неэластичный | Темп роста спроса меньше темпа снижения цены | Темп снижения спроса меньше темпа роста цены |
| η = 0 | Совершенно неэластичный | Совершенно не изменяется объем закупок | Совершенно не изменяется объем закупок |
1. Чем больше товаров, являющихся, с точки зрения покупателя, заменителями данного, тем эластичнее спрос. Например, спрос на мыло определенной марки. Если цена на эту марку мыла повысится, то большинство покупателей безболезненно перейдут на другие сорта, хотя кто-то, возможно, останется верен своей привычке (вот почему так важен оборот "с точки зрения покупателя" в первой фразе этого пункта). Другой пример - магнитофоны. Спрос на импортную аудиотехнику на черном рынке достаточно эластичен.
Однако представим себе, что подобные устройства вообще не выпускались бы в России. Думается, покупатели были бы более снисходительны.
Отсюда следует и такой вывод: чем более агрегированный товар мы рассматриваем, тем ниже эластичность. Так, спрос на мыло вообще малоэластичен (его заменить нечем), однако спрос на мыло "Консул" может иметь весьма высокую эластичность.
2. Чем выше доля расходов на данный товар в бюджете потребителя, тем выше эластичность. Если потребитель расходует на данный товар незначительную часть своего бюджета, ему не нужно изменять свои привычки и пристрастия при изменении цены. С этой точки зрения интересна история такого товара, как соль. Совершенная неэластичность спроса на соль отмечалась в разделе 0. Но так было не всегда. В середине XIX в. в России пуд соли стоил от 50 коп. до 1 руб. из-за высокого налога на соляное производство. Для многих, особенно в деревне, это было непомерно дорого. После отмены акцизного налога в 1880 г. цена соли упала в два раза, а потребление выросло на 70 %.
Но одна и та же сумма при большом доходе составила бы малую долю бюджета, а при низком доходе - значительную. Поэтому эластичность спроса на один и тот же товар у потребителей с высоким доходом меньше, чем с низким.
3. Эластичность спроса ниже всего у тех товаров, которые, с точки зрения потребителя, являются необходимыми. Речь тут идет не только о хлебе. Для одного необходимыми товарами являются табак и алкоголь, для другого - марки и спичечные этикетки, для третьего - джинсы "Levi Strauss". Это дело вкуса.
Разновидностью данной закономерности является особенно низкая эластичность спроса на те товары, потребление которых (опять-таки с точки зрения потребителя) не может быть отложено. "Мне очень нужно" плюс "мне срочно нужно" - и покупатель становится сговорчивым. Пример: спрос на цветы 8 марта, 1 сентября и т.п.
Ранее мы разделяли эластичность на высокую и низкую, сравнивая ее абсолютное значение с единицей. Значение η = 1 интересно во многих отношениях. Одна из его особенностей обнаруживается при анализе зависимости от цены суммарных расходов потребителей R(P) = PD(P) на приобретение данного товара.
Формула (5) (см. МП, II) показывает, что Εp[R] = Εp[D] + 1. Это значит, что при Εp[D] >-1 (т. е. при низкой эластичности, η < 1) затраты возрастают при увеличении цены, а при Εp[D] < -1 (т. е. при высокой эластичности, η > 1) - убывают: резкая реакция покупателей на возрастание цены приводит к сокращению объема спроса более значительному, чем вызвавшее его повышение цены.
Таблица 2. Общие расходы при изменениях цен
| Εp[D] | η | Характер спроса | dR/dP | Изменение общих расходов | |
| При уменьшении цены | При увеличении цены | ||||
| Εp[D]< -1 | >1 | Эластичный | <0 | Возрастают | Уменьшаются |
| Εp[D]=1 | =1 | Единичная эластичность | Не изменяются | Не изменяются | |
| Εp[D]> -1 | <1 | Неэластичный | >0 | Уменьшаются | Возрастают |
Постоянной эластичностью n = 1 обладает степенная функция с показателем степени - 1 (см. МП, II, формула (9) и упражнение 3), т. е. обратная пропорциональность D(P) = а / Р.
Непосредственно видно, что для такой функции спроса справедливо равенство:
R(P) = P·a/p = a ,
т. е. суммарные расходы на приобретение товара не зависят от его цены.
Если эластичность спроса на товар - переменная величина, то суммарные расходы будут возрастающей функцией цены на участках с низкой эластичностью и убывающей - на участках с высокой эластичностью. Максимумам суммарных расходов (переходам от возрастания к убыванию) и минимумам (обратным переходам) соответствуют цены, при которых η = 1.
В качестве иллюстрации рассмотрим линейную функцию спроса (рис. 2,а).
Эта функция имеет постоянную производную, но ее эластичность изменяется во всем диапазоне возможных значений: когда цена стремится к нулю, эластичность также стремится к нулю, по мере приближения к цене P0 эластичность стремится к бесконечности. В середине этого интервала, т. е. при Р =P0 / 2, выполняется равенство η = 1 (см. МП, II, упражнение 1), и суммарные расходы принимают наибольшее значение. На рис. 2,б представлен график функции суммарных расходов R(P) и показано положение максимума.
Читатель может самостоятельно в качестве упражнения представить функцию спроса в аналитической форме и после необходимых выкладок убедиться в том, что суммарные расходы будут максимальными в указанной на рисунке точке.
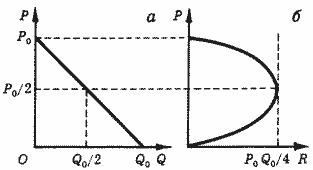
Рис. 2. Линейная функция спроса (а) и функция суммарных расходов (б).
До сих пор мы интересовались зависимостью объема спроса на определенный товар от цены на этот товар. В действительности же спрос зависит от многих факторов. В качестве важнейших из них можно выделить цены на другие товары и доходы потребителей. При анализе зависимости спроса от этих факторов также широко используется аппарат эластичности.
Мерой реакции спроса на данный товар на изменение цены некоторого другого товара служит перекрестная (или взаимная) эластичность спроса по цене. Для ее определения может быть использована уже знакомая нам формула (1), с тем лишь отличием, что объем спроса (Q) относится к одному товару, а цена (Р) - к другому. Спрос на данный товар при увеличении цены на другой товар может и возрастать, и убывать - в зависимости от отношения потребителя к совместному использованию того и другого товара. Например, рост цены на бензин должен снижать спрос на автомобили; в то же время повышение цены на хозяйственное мыло увеличивает спрос на стиральный порошок. Таким образом, перекрестная эластичность может быть и положительной, и отрицательной, и ее знак представляет не меньший интерес, чем абсолютная величина. Первый пример относился к взаимодополняемым товарам; для них характерна отрицательная перекрестная эластичность. Во втором примере речь идет о взаимозамещаемых товарах; здесь мы обычно сталкиваемся с положительной перекрестной эластичностью. Теперь обратимся к эластичности спроса по доходам. Ее можно определить аналогично эластичности спроса по цене:
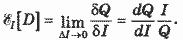 , (4) , (4)
|
Здесь Q - объем спроса на определенный товар, I - доход потребителя, символ δ, как и раньше, обозначает относительные приращения. Такие зависимости обычно изучают путем сопоставления спроса в группах потребителей, каждая из которых более или менее однородна по уровню дохода.
Рост дохода увеличивает возможность совершения покупок, так что спрос на большинство товаров с увеличением дохода возрастает, и эластичность спроса по доходам оказывается положительной. Но по абсолютной величине эти эластичности могут резко различаться. Эластичность спроса на товары первой необходимости весьма мала, а на предметы роскоши - велика. Кроме того, существуют товары, которые при достаточно высоком уровне доходов вытесняются лучшими товарами-заменителями, и спрос на них при дальнейшем увеличении дохода падает. На этом участке эластичность оказывается отрицательной. Такие товары называют низшими благами (рис. 3).
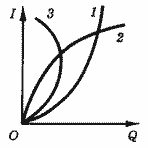
Рис. 3. Зависимости спроса (Q) от доходов (I). 1 - товары первой необходимости (ΕI <1); 2 - предметы роскоши (ΕI > 1); 3 - низшие блага (ΕI<0 при больших доходах).
Итак, мы видим, что такой показатель, как эластичность спроса, служит весьма полезным инструментом выявления отношения потребителей к различным товарам. Но этот же инструмент может быть использован и для анализа предложения.
Эластичность предложения по цене:
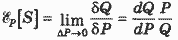 , (5) , (5)
|
определяется аналогично эластичности спроса, но здесь Q - объем предложения, связанный с ценой функцией Q = S(P) (рис. 4). Так как объем предложения - неубывающая функция цены, эластичность предложения в обычных случаях - неотрицательная величина. В лекции 6 отмечался различный характер функции предложения в различных периодах. Это различие находит свое отражение в эластичности:
а) для мгновенного предложения, когда продукт уже произведен, его количество является величиной постоянной, Εp[S] = 0;
б) в коротком периоде предложение может в некоторой степени приспособиться к изменяющейся цене и на значительной части кривой предложения Εp[S] = 0 ; однако при этом возможности производства не безграничны, и по мере приближения к предельно возможному объему Q* (рис. 4) эластичность снижается, стремясь к нулю;
в) в длительном периоде возможности приспособления еще шире, а коэффициент эластичности больше, чем в среднем периоде. Ограниченность возможностей предложения при этом обычно не играет существенной роли.
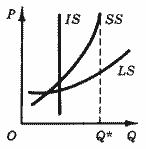
Рис. 4. Кривые предложения в различных периодах:мгновенном (IS), коротком (SS) и длительном (LS).
Дата добавления: 2015-12-29; просмотров: 814;
