Законы рассеяния (распределения) размеров
В результате возникновения случайных погрешностей при обработке партии заготовок на настроенном станке истинный размер каждой заготовки является случай величиной и может принимать любое значение в границах определенного интервала.
Совокупность значений истинных размеров заготовок, обработанных неизменных условиях и расположенных в возрастающем порядке с указанием частоты повторения этих размеров или частостей, называется распределением размеров заготовок. Под частостью понимается отношение числа заготовок одного размера к общему числу заготовок партии.
Распределение размеров заготовок можно представить в виде таблиц или графиков. На практике измеренные значения истинных размеров заготовок разбивают на интерн или разряды таким образом, чтобы цена интервала (разность между наибольшим и наименьшим размерами в пределах одного интервала) была несколько больше и деления шкалы измерительного устройства. Этим компенсируются погрешности измерения. Частость в этом случае представляет собой отношение числа m заготовок действительные размеры которых попали в данный интервал, к общему количеству n измеренных заготовок партии.
Например, после измерения 100 шт. заготовок с действительными размерами в пределах от 20,00 до 20,35 мм распределение размеров этих заготовок может иметь приведенный в табл. 3.3.
Таблица 3.3.
Распределение размеров заготовок
| Интервал, мм | Частота т | Частость rn/n |
| 20,00-20,05 | 0,02 | |
| 20,05-20,10 | 0,11 | |
| 20,10-20,15 | 0,19 | |
| 20,15-20,20 | 0,28 | |
| 20,20-20,25 | 0,22 | |
| 20,25-20,30 | 0,15 | |
| 20,30-20,35 | 0,03 | |
| Итого: | п =2Г-т = 100 | JET т/п |
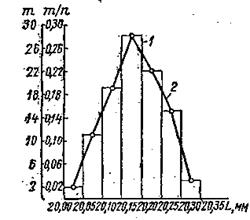
Рис. 3.9 Распределение измеренных размеров заготовок
Распределение измеренных размеров таких заготовок можно представтъ в графика (рис.3. 9). По оси абсцисс откладывают интервалы размеров в соответственно табл.3. 3, а по оси ординат соответствующие им частоты т или частоты т п. В результате построения получается ступенчатая линия 1, называемая гистограммы! распределения. Если последовательно соединить между собой точки, соответствующие середине каждого интервала, то образуется ломаная кривая, которая носит название эмпирической кривой распределения, или полигона 2 распределения. При значительном количестве замере заготовок и большом числе интервалов размеров ломаная эмпирическая кривая приближается по форме к плавной кривой, именуемой кривой распределения, построения гистограммного распределения рекомендуется измеренные размеры разбивать не менее чем на шесть интервалов при общем числе измеряемых заготовок не меньше 50 шт.
При разных условиях обработки заготовок рассеяние их истинных размеров подчиняется различным математическим законам. В технологии машиностроения большое практическое значение имеют следующие законы: нормального распределения (закон Гаусса), равнобедренного треугольника (закон Симпсона). эксцентриситета (закон Релея), законы равной вероятности и функции распределения, представляющие с композицию этих законов.
Закон нормального распределения(закон Гаусса).
Многочисленные исследования, проведенные профессорами А.Б. Яхиным, А.А. Зыковым и другими, показали, что распределение действительных размеров заготовок, обработанных на настроенных станках, очень часто подчиняется закону нормального распределения (закону Гаусса).
Это объясняется известным положением теории вероятностей о том, распределение суммы большого числа взаимно независимых случайных слагаемых величин (при ничтожно малом и примерно одинаковом влиянии каждой из них на общую сумму и при отсутствии влияния доминирующих факторов) подчиняется закону нормального распределения Гаусса.
Результирующая погрешность обработки обычно формируется в результате одновременного воздействия большого числа погрешностей, зависящих от станка, приспособления, инструмента и заготовки, которые по существу представляют с взаимно независимые случайные величины; влияние каждой из них на результирующую погрешность имеет один порядок, поэтому распределение результирующей погрепп обработки, а значит, и распределение действительных размеров обрабатываемых заготовок подчиняются закону нормального распределения.
Уравнение кривой нормального распределения имеет следующий вид:
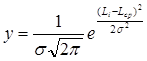
 где σ - среднее квадратическое отклонение, определяемое по формуле:
где σ - среднее квадратическое отклонение, определяемое по формуле:
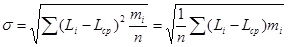
Li - текущий действительный размер; Lcp - среднее взвешенное арифметическое значение действительных размеров заготовок данной партии. Значение Lcp можно определить из выражения:
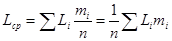
|
|
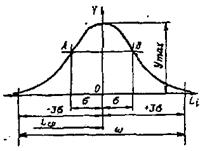
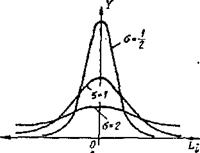
| Рис.3.10. Кривая нормального распределения (закон Гаусса) | Рис.3.11 Влияние среднего квадратического отклонения на форму кривой нормального распределения |
где mi - частота (количество заготовок данного интервала размеров); n - количество заготовок в партии.
Кривая, характеризующая дифференциальный закон нормального распределения, показана на рис.3.10. Среднее арифметическое Lcp действительных размеров заготовок данной партии характеризует положение центра группирования размеров.
Анализ уравнения (3.2) показывает, что кривая нормального распределения симметрична относительно оси ординат. Значениям х и -х соответствует одинаковая величина ординаты у. При Li = Lcp кривая имеет максимум, равный:
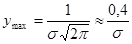 (3.5)
(3.5)
На расстоянии ±σ от вершины кривая имеет две точки перегиба (точки А и В). Ордината точек перегиба:
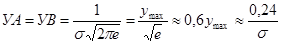 (3.6)
(3.6)
Кривая ассимптотически приближается к оси абсцисс. На расстоянии ±3σ от положения вершины кривой ее ветви так близко подходят к оси абсцисс, что в этих пределах оказывается 99,73% площади, заключенной между всей кривой нормального распределения с осью абсцисс, ограничивая 100% площади между кривой и осью абсцисс. Возникающая при этом допущении погрешность, составляющая 0,27%, практического значения не имеет.
При увеличении σ значение ординаты у^ уменьшается (см. формулу 3.9), а поле рассеяния о = 6а возрастает; в результате этого кривая становится более пологой и низкой, что свидетельствует о большем рассеянии размеров и, следовательно, о меньшей точности. В этом смысле среднее квадратическое отклонение а является мерой рассеяния или мерой точности. Влияние σ на форму кривой нормального распределения показано на рис.3.11.
Фактическое поле рассеяния размеров заготовок ω = 6σ
Закон равнобедренного треугольника (закон Симпсона). При обработке заготовок с точностью 7-го и 8-го, а в некоторых случаях и 6-го квалитетов распределение их размеров в большинстве случаев подчиняется закону Симпсона, который графически выражается равнобедренным треугольником (рис.3.15, а) с полем рассеяния
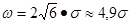 (3.7)
(3.7)
Величина среднего квадратического отклонения σ и в этом случае определяется по формуле (3.3).
- 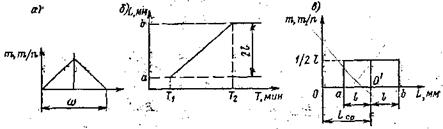
Рис.3.12 Распределение размеров обработанных заготовок по закону Симпсона а) и по закону равной вероятности б), в)
Закон равной вероятности. Если рассеяние размеров зависит только от переменных систематических погрешностей (например, от износа режущего инструмента), то распределение действительных размеров партии обработанных заготовок подчиняется закону равной вероятности.
Например, при установившемся износе режущего инструмента уменьшение его размеров во времени подчиняется прямолинейному закону, что соответственно увеличивает (при обработке валов) или уменьшает (при обработке отверстий) диаметры обрабатываемых заготовок
Естественно, что изменение размеров обрабатываемых заготовок на величину 21 = b - а за период Т2 - Т1 в этом случае тоже происходит по закону прямой линии (рис.3.12, б). Распределение размеров заготовок в интервале от а до b по закону равной вероятности выражается прямоугольником (рис.3.12, в) с основанием 21 и высотой (ординатой) 1/21.
Площадь прямоугольника равна единице что означает 100%-ную вероятность появления размера заготовки в
интервале от а до Ь.
Среднее арифметическое значение размера:
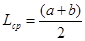 (3.8)
(3.8)
Среднее квадратическое:
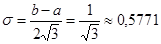 (3.9)
(3.9)
Фактическое поле рассеяния:
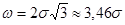 (3.10)
(3.10)
Закон равной вероятности распространяется на распределение размеров заготовок повышенной точности (5-6-й квалитеты и выше) при их обработке по методу пробных ходов. Из-за сложности получения размеров очень высокой точности вероятность попадания размера заготовки в узкие границы допуска по среднему, наибольшему или наименьшему его значению становится одинаковой.
Закон эксцентриситета (закон Релея). Распределение таких существенно положительных величин, как эксцентриситет, биение, разностенность, непараллельность, неперпендикулярность, овальность, конусообразность и некоторых других, характеризующихся их абсолютными значениями (то есть без учета знака), подчиняется закону распределения эксцентриситета (закону Релея).
Распределение по закону Релея формируется (в частности) тогда, когда случайная величина R является радиус-вектором при двумерном гауссовом распределении, то есть если она представляет собой геометрическую сумму двух. случайных величин х и у
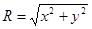 , (3.11)
, (3.11)
каждая из которых подчиняется закону Гаусса с параметрами:
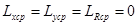
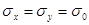
Закон распределения Релея однопараметрический, и уравнение его кривой распределения имеет вид
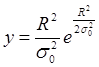 (3.12)
(3.12)
где σ0 - среднее квадратическое отклонение значении координат х и у.
На рис.3.13, б) показано, что для теоретической кривой распределения по закону Релея характерны крутой подъем восходящей ветви и более пологий спуск нисходящей ветви. Вершина кривой более заострена, чем у кривой нормального распределения, и смещена от среднего значения переменной величины R в сторону начала координат.
Из уравнения (3.12) следует, что при R=0 и у=0, то есть начало кривой распределения эксцентриситета совпадает с началом координат. Нисходящая ветвь этой кривой асимптотически приближается к оси абсцисс.
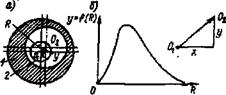
Рис.3.13. Образование эксцентриситета (радиуса-вектора R) втулки 1 при ее обработке на цилиндрической оправке 2 при различии зазора между оправкой и отверстием втулки (а) и функции y=f (R) распределения размеров по закону Релея (б).
Дата добавления: 2015-12-26; просмотров: 7812;
