Формулы средней ошибки выборки.
В связи с тем, что признаки в изучаемой совокупности варьируют, то состав единиц, попавших в выборку, может не совпадать с составом единиц всей совокупности. Это означает, что Р и 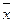 не совпадают с W и
не совпадают с W и 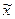 . Возможное расхождение между этими характеристиками определяется ошибкой выборки, которая определяется по формуле:
. Возможное расхождение между этими характеристиками определяется ошибкой выборки, которая определяется по формуле:
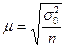
где 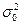 - генеральная дисперсия.
- генеральная дисперсия.
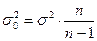
где 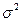 - выборочная дисперсия.
- выборочная дисперсия.
Отсюда видно, где генеральная дисперсия отличается от выборочной дисперсии в 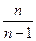 раз.
раз.
Существует повторный и бесповторный отбор. Сущность повторного отбора состоит в том, что каждая, попавшая в выборку единица, после наблюдения возвращается в генеральную совокупность и может быть исследована повторно. При повторном отборе средняя ошибка выборки рассчитывается:
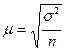
Для показателя доли альтернативного признака дисперсия выборки определяется по формуле:
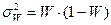
На практике повторный отбор применяется редко. При бесповторном отборе, численность генеральной совокупности N в ходе выборки сокращается, формула средней ошибки выборки для количественного признака имеет вид:
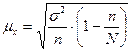 , тогда
, тогда 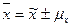
Одно из возможных значений, в которых может находиться доля изучаемого признака равно:
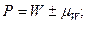
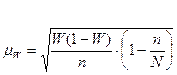
где 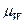 - ошибка выборки альтернативного признака.
- ошибка выборки альтернативного признака.
Пример.
При выборочном обследовании 10 % изделий партии готовой продукции по методу без повторного отбора получены следующие данные о содержании влаг в образцах.
| Влажность % | Число образцов | хi |
| До 13 | ||
| 13-15 | ||
| 15-17 | ||
| 17-19 | ||
| 19 и выше | ||
Определить средний % влажности, дисперсию, среднее квадратическое отклонение, с вероятностью 0,954 возможные пределы, в которых ожидается ср. % влажности всей готовой продукции, с вероятность 0,987 возможные пределы удельного веса стандартной продукции при условии, что к нестандартной партии относятся изделия с влажностью до 13 и выше 19 %.
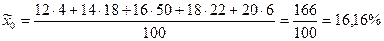
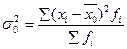
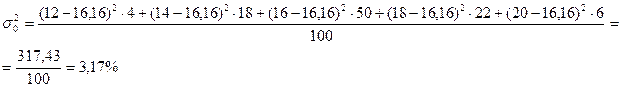
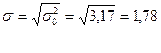
Лишь с определенной вероятностью можно утверждать, что генеральная доля от выборочной доли и генеральная средняя от выборочной средней, отклоняются в t раз.
В статистике эти отклонения называются предельнымиошибкамивыборки и обозначаются 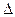 .
.
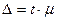
Вероятность суждений можно повысить или понизить в t раз. При вероятности 0,683 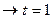 , при 0,954
, при 0,954 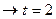 , при 0,987
, при 0,987 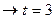 , тогда показатели генеральной совокупности по показателям выборки определяются:
, тогда показатели генеральной совокупности по показателям выборки определяются:
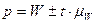
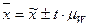
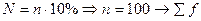
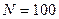
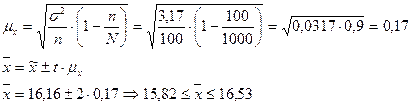
Средний процент влажности генеральной совокупности может быть любым значением, находящемся в пределах от 15,82 до 16,33.
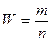 ;
; 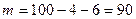
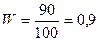
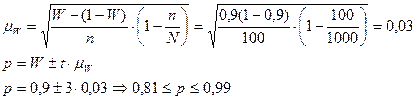
Таким образом, удельный вес стандартных изделий в генеральной совокупности находится в пределах 81 % – 99 %.
Из расчета задачи видно, что возможные пределы удельного веса единиц генеральной совокупности будут находиться:
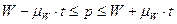
А среднее значение генеральной совокупности находится в пределах :
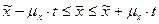
Дата добавления: 2015-12-26; просмотров: 1069;
