Методические рекомендации по чтению лекций
Предусмотрено сочетание традиционных видов учебной активности, таких как конспектирование лекций и контроль усвоения теоретического материала в виде коллоквиумов, так и интерактивных технологий, таких как собеседования, ситуационные игры на выбор методов защиты информации на практических занятиях.
Подготовка студентами докладов по темам, не входящим в план лекций, а также выполнение расчетных работ, позволяют расширить научный кругозор студентов, повысить навык работы с учебной и научной отечественной и зарубежной литературой, развить языковые навыки, повысить математическую подготовку, укрепить междисциплинарные связи, повысить навык программирования
В условиях интеграции автоматизированных систем в глобальное информационное пространство актуальными являются проблемы их информационной безопасности. Поэтому будущий специалист специальности 090202 в рамках изучения дисциплины «Теория информации» должен знать аксиоматические определения понятия информации, её свойства, алгоритмы кодирования источника, алгоритмы сжимающего кодирования, алгоритмы помехоустойчивого кодирования, уметь вычислять предельные соотношения для систем передачи данных. Знания и умения, полученные студентами при изучении этой дисциплины, используются при изучении теории защиты информации, основ информационной безопасности систем и телекоммуникаций, безопасности вычислительных сетей, комплексного обеспечения информационной безопасности автоматизированных систем.
Содержание дисциплины «Основы теории информации» включает следующие темы, изучаемые на лекциях:
Тема 1.1. Формальное представление знаний. Виды информации.
Тема 1.2. Способы измерения информации.
Тема 2.1. Теорема отчетов
Тема 2.2. Смысл энтропии Шеннона.
Тема 3.1. Сжатие информации.
Тема 3.2. Арифметическое кодирование.
Тема 4.1. Стандарты шифрования данных. Криптография.
Методические рекомендации по разделу 1.
Базовые понятия теории информации
Алфавитный подход
В курсе знакомство учащихся с алфавитным подходом к измерению информации чаще всего происходит в контексте компьютерного представления информации. Основное утверждение звучит так:
Количество информации измеряется размером двоичного кода, с помощью которого эта информация представлена
Поскольку любые виды информации представляются в компьютерной памяти в форме двоичного кода, то это определение универсально. Оно справедливо для символьной, числовой, графической и звуковой информации.
Один знак (разряд) двоичного кода несет 1 бит информации.
При объяснении способа измерения информационного объема текста в базовом курсе данный вопрос раскрывается через следующую последовательность понятий: алфавит — размер двоичного кода символа — информационный объем текста.
Логика рассуждений разворачивается от частных примеров к получению общего правила. Пусть в алфавите некоторого языка имеется всего 4 символа. Обозначим их: 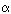 ,
, 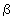 ,
, 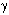 ,
, 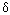 . Эти символы можно закодировать с помощью четырех двухразрядных двоичных кодов:
. Эти символы можно закодировать с помощью четырех двухразрядных двоичных кодов: 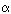 — 00,
— 00, 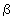 — 01,
— 01, 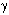 — 10,
— 10, 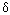 — 11. Здесь использованы все варианты размещений из двух символов по два, число которых равно 22 = 4. Отсюда делается вывод: информационный вес символа из 4-символьного алфавита равен двум битам.
— 11. Здесь использованы все варианты размещений из двух символов по два, число которых равно 22 = 4. Отсюда делается вывод: информационный вес символа из 4-символьного алфавита равен двум битам.
Следующий частный случай — 8-символьный алфавит, каждый символ которого можно закодировать 3-разрядным двоичным кодом, поскольку число размещений из двух знаков группами по 3 равно 23 = 8. Следовательно, информационный вес символа из 8-символьного алфавита равен 3 битам. И т.д.
Обобщая частные примеры, получаем общее правило: с помощью b-разрядного двоичного кода можно закодировать алфавит, состоящий из N = 2b — символов.
Пример 1. Для записи текста используются только строчные буквы русского алфавита и “пробел” для разделения слов. Какой информационный объем имеет текст, состоящий из 2000 символов (одна печатная страница)?
Решение. В русском алфавите 33 буквы. Сократив его на две буквы (например, “ё” и “й”) и введя символ пробела, получаем очень удобное число символов — 32. Используя приближение равной вероятности символов, запишем формулу Хартли:
2i =32 = 25
Отсюда: i = 5 бит — информационный вес каждого символа русского алфавита. Тогда информационный объем всего текста равен:
I = 2000 · 5 = 10 000бит
Пример 2. Вычислить информационный объем текста размером в 2000 символов, в записи которого использован алфавит компьютерного представления текстов мощностью 256.
Решение. В данном алфавите информационный вес каждого символа равен 1 байту (8 бит). Следовательно, информационный объем текста равен 2000 байт.
В практических заданиях по данной теме важно отрабатывать навыки учеников в пересчете количества информации в разные единицы: биты — байты — килобайты — мегабайты — гигабайты. Если пересчитать информационный объем текста из примера 2 в килобайты, то получим:
2000 байт = 2000/1024 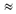 1,9531 Кб
1,9531 Кб
Пример 3. Объем сообщения, содержащего 2048 символов, составил 1/512 часть мегабайта. Каков размер алфавита, с помощью которого записано сообщение?
Решение. Переведем информационный объем сообщения из мегабайтов в биты. Для этого данную величину умножим дважды на 1024 (получим байты) и один раз — на 8:
I = 1/512 · 1024 · 1024 · 8 = 16 384 бита.
Поскольку такой объем информации несут 1024 символа (К), то на один символ приходится:
i = I/K = 16 384/1024 = 16 бит.
Отсюда следует, что размер (мощность) использованного алфавита равен 216 = 65 536 символов.
Объемный подход
Можно оставить знания учащихся об объемном подходе к измерению информации на том же уровне, что описан выше, т.е. в контексте объема двоичного компьютерного кода.
При изучении на профильном уровне объемный подход следует рассматривать с более общих математических позиций, с использованием представлений о частотности символов в тексте, о вероятностях и связи вероятностей с информационными весами символов.
Знание этих вопросов оказывается важным для более глубокого понимания различия в использовании равномерного и неравномерного двоичного кодирования
Пример 4. В алфавите племени ЗУМУ всего 4 буквы (А, У, М, К), один знак препинания (точка) и для разделения слов используется пробел. Подсчитали, что в популярном романе “Зумука” содержится всего 10 000 знаков, из них: букв А — 4000, букв У — 1000, букв М — 2000, букв К — 1500, точек — 500, пробелов — 1000. Какой объем информации содержит книга?
Решение.Поскольку объем книги достаточно большой, то можно допустить, что вычисленная по ней частота встречаемости в тексте каждого из символов алфавита характерна для любого текста на языке МУМУ. Подсчитаем частоту встречаемости каждого символа во всем тексте книги (т.е. вероятность) и информационные веса символов
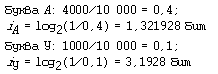

Общий объем информации в книге вычислим как сумму произведений информационного веса каждого символа на число повторений этого символа в книге:

Дата добавления: 2015-12-26; просмотров: 889;
