Криптосистема с открытым ключом
Первую и наиболее известную систему с открытым ключом разработали в 1978 году американцы Р. Ривест (Rivest R.), Э. Шамир (Shamir A.) и Л. Адлеман (Adleman L.). По их именам эта система получила название RSA.
Пусть абоненты  и
и 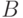 решили организовать для себя возможность секретной переписки. Для этого каждый из них независимо выбирает два больших простых числа (
решили организовать для себя возможность секретной переписки. Для этого каждый из них независимо выбирает два больших простых числа ( 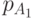 ,
,  и
и  ,
,  ), находит их произведение (
), находит их произведение ( 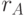 и
и  ),функцию Эйлера от этого произведения (
),функцию Эйлера от этого произведения ( 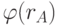 и
и 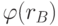 ) и случайное число (
) и случайное число ( 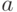 и
и 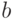 ), меньшее вычисленного значения функции Эйлера и взаимно простое с ним. Кроме того,
), меньшее вычисленного значения функции Эйлера и взаимно простое с ним. Кроме того,  из уравнения
из уравнения  находит
находит  (
( 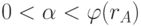 ), а
), а 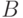 из уравнения
из уравнения  находит
находит 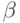 (
(  ). Затем
). Затем  и
и 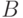 печатают доступную всем книгу паролей вида:
печатают доступную всем книгу паролей вида:
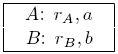
Теперь кто-угодно может отправлять конфиденциальные сообщения  или
или 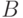 . Например, если пользователь книги паролей хочет отправить сообщение
. Например, если пользователь книги паролей хочет отправить сообщение 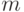 для
для 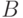 (
( 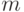 должно быть меньшим
должно быть меньшим  , или делиться на куски, меньшие
, или делиться на куски, меньшие  ), то он использует ключ
), то он использует ключ 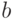 из книги паролей для получения шифрованного сообщения
из книги паролей для получения шифрованного сообщения 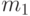 по формуле
по формуле 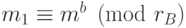 , которое и отправляется
, которое и отправляется 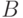 .
. 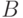 для дешифровки
для дешифровки 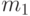 использует ключ
использует ключ 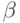 в формуле
в формуле 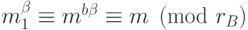 , т.к.
, т.к.  , следовательно,
, следовательно,  для некоторого целого
для некоторого целого 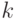 и
и 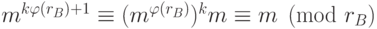 , т.к.
, т.к. 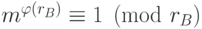 по теореме Эйлера-Ферма. Доказано1 что задача нахождения секретного ключа
по теореме Эйлера-Ферма. Доказано1 что задача нахождения секретного ключа 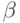 по данным из книги паролей имеет ту же сложность, что и задача разложения числа
по данным из книги паролей имеет ту же сложность, что и задача разложения числа  на простые множители.
на простые множители.
Пример. Пусть для 
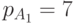 и
и 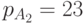 , тогда
, тогда 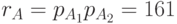 ,
,  ,
,  ,
, 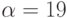 (из уравнения
(из уравнения 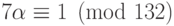 ). Следовательно, запись в книге паролей для
). Следовательно, запись в книге паролей для  будет иметь вид
будет иметь вид 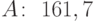 . Если кто-то захочет отправить
. Если кто-то захочет отправить  секретное сообщение
секретное сообщение  , то он должен сначала превратить его в шифровку
, то он должен сначала превратить его в шифровку 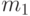 по формуле
по формуле 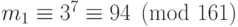 . Когда
. Когда  получит
получит 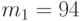 он дешифрует его поформуле
он дешифрует его поформуле 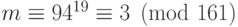 .
.
Упражнение 49 Нужно послать секретные сообщения 25 и 2 для JB и 14 для CIA, используя следующие записи открытой книги паролей криптосистемы RSA:
JB: 77,7;
CIA: 667,15.
Упражнение 50 Пользователь системы RSA выбрал  и
и  . Какие из чисел 12, 33, 125, 513 он может выбрать для открытого ключа? Вычислить для них закрытый ключ.
. Какие из чисел 12, 33, 125, 513 он может выбрать для открытого ключа? Вычислить для них закрытый ключ.
Упражнение 51 Пользователь системы RSA, выбравший  ,
,  и
и 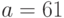 , получил шифрованное сообщение
, получил шифрованное сообщение 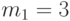 . Дешифровать
. Дешифровать 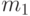 .
.
Дата добавления: 2015-12-26; просмотров: 1251;
