Тема 2.1.1. Теорема отсчетов Котельникова и Найквиста — Шеннона
Базисным понятием всей теории информации является понятие энтропии. Энтропия – мера неопределенности некоторой ситуации. Можно также назвать ее мерой рассеяния и в этом смысле она подобна дисперсии. Но если дисперсия является адекватной мерой рассеяния лишь для специальных распределений вероятностей случайных величин (а именно – для двухмоментных распределений, в частности, для гауссова распределения), то энтропия не зависит от типа распределения. С другой стороны, энтропия вводится так, чтобы обладать, кроме универсальности и другими желательными свойствами. Так, если некий опыт имеет n равновероятных исходов, а другой опыт m равновероятных исходов, то составной опыт имеет nm таких исходов. Если мы вводим меру неопределенности f , то естественно потребовать, чтобы она была такова, чтобы во-первых, неопределенность росла с ростом числа возможных исходов, а во-вторых, неопределенность составного опыта была равна просто сумме неопределенности отдельных опытов, иначе говоря, мера неопределенности была аддитивной: f(nm)=f(n)+f(m). Именно такая удобная мера неопределенности была введена К. Шенноном:
H(X)= — 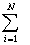 P (Xi) log P (Xi),
P (Xi) log P (Xi),
где Х – дискретная случайная величина с диапазоном изменчивости N, P(Xi) – вероятность i – го уровня X.
В дальнейшем мы будем рассматривать Х как некоторую физическую величину, меняющуюся во времени или пространстве. Временной или пространственный ряд Xj (j – индекс временной или пространственной координаты r) будем называть, как это принято в ряде естественных наук, “вариацией”. В самой теории информации такое пространственно-временное упорядочение совершенно не обязательно, но, во-первых, анализ именно таких вариаций составляет суть всех естественных наук, во-вторых, это с первых шагов позволяет лучше ощутить смысл новых понятий. Заметим также, что если даже пространственная или временная упорядоченность величины Х в явном виде отсутствует, она неизбежно существует неявно. Например, положим, что j– номер различимой частицы, а Хj – ее импульс. Х – неупорядоченная случайная величина (ее номер j присваивается произвольно), но все эти частицы неизбежно разнесены в пространстве (раз мы можем их различить) и, при необходимости, мы можем их соединить некоторой (ломаной) осью и восстановить упорядоченность. Но для понимания проще представлять Х как сигнал, который может быть записан самописцем, как рельеф местности вдоль некоторого профиля, как пространственное распределение плотности энергии поля и т.п.
Таким образом, чтобы рассчитать H(X), берется запись вариации Xj , разность между максимальным и минимальными значениями Хj разбивается на N квантов (обычно равных разрешающей способности прибора) и подсчитывается число mi заполнения каждого i -го уровня (число благоприятных случаев). Общее число случаев M – это число пространственных или временных ячеек, опять-таки обычно определяемых разрешением прибора. В результате мы получаем распределение вероятностей P(Xi)=mi/M, которое подставляем в формулу H(x).
В теории информации в формуле для энтропии обычно используют двоичные логарифмы, тогда (энтропия и информация) измеряется в битах. Это удобно тем, что выбор между двумя равновероятными уровнями Xi (как в двоичном) сигнале характеризуется неопределенностью 1 бит. В популярной литературе иногда пользуются десятичными логарифмами и единицей энтропии является дит. В физике удобнее пользоваться натуральными логарифмами и единицей энтропии является нат (поскольку в дальнейшем наш подход существенно физический, мы также используем натуральные логарифмы). Выбор основания – лишь вопрос масштаба, в любом случае энтропия безразмерна. Возможная величина энтропии заключена в пределах:
0£ H(X)£ logN.
Нижняя грань соответствует вырожденному распределению. Неопределенность величинs Х отсутствует. В вариационном ряду это соответствует Xj=const.Верхняя грань соответствует равномерному распределению. Все N значений Xi встречаются с равной вероятностью. В вариационном ряду это может соответствовать, в частности, линейному тренду Xj=arj.
Если две случайные величины X и Y, каким-то образом связанные друг с другом (например на входе и выходе какой-то системы) , то знание одной из них, очевидно уменьшает неопределенность значений другой. Остающаяся неопределенность оценивается условной энтропией. Так, условная энтропия Х при условии знания Y определяется как:
H(X|Y)= 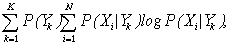
где 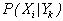 – условные вероятности (вероятность i-го значения X при условии Y=Yk), диапазоны изменчивости X и Y (соответственно N и K) не обязательно совпадают.
– условные вероятности (вероятность i-го значения X при условии Y=Yk), диапазоны изменчивости X и Y (соответственно N и K) не обязательно совпадают.
Чтобы рассчитать H(X|Y), рассчитывают К энтропий Х, соответствующих фиксированному Yk и затем суммируют результаты с весами P(Yk). Очевидно, условная энтропия меньше безусловной, точнее:
0£ H(X|Y)£ H(X).
Нижняя грань соответствует однозначной зависимости Х от Y, верхняя – полной независимости.
Информация определяется разностью между безусловной и условной энтропиями. Это уменьшение неопределенности “знания чего-то за счет того, что известно что-то”. При этом замечательно, что информация I симметрична, т.е. IYX=IXY:
IXY=H(X)-H(X|Y)=H(Y)-H(Y|X)= IYX.
Информация всегда неотрицательна; она равна нулю, когда Х и Y независимы; информация максимальна и равна безусловной энтропии, когда между Х и Yимеется однозначная зависимость. Таким образом, безусловная энтропия – это максимальная информация, потенциально содержащаяся в системе (вариационном ряде). Заметим, что мы сказали однозначная, но не взаимно-однозначная зависимость. Это значит, что несмотря на симметрию, верхние граниIXY и IYX отличаются:
0£ IXY£ H(X), 0£ IYX£ H(Y).
Как это может быть? Положим, XÞ Y (но обратное неверно). Тогда H(Y|X)=0, H(X|Y)¹ 0, IYX=H(Y)= IXY. Очевидно, это возможно только когда H(X)>H(Y).
Информация – это всего лишь характеристика степени зависимости некоторых переменных, ничего более загадочного в ней нет. Зато это предельно общая характеристика. Ее можно сравнить с корреляцией, но если корреляция характеризует лишь линейную связь переменных, информация характеризует любуюсвязь . Тип связи может быть совершенно любым и, более того, неизвестным нам. Это не помешает рассчитать информацию, количественно сравнивать между собой разнотипные зависимости и т.д. Платой за общность является лишь невозможность, зная количество информации написать уравнение связи переменных (в отличие от того, как корреляция позволяет легко переходить к регрессии). Можно определить и совместную энтропию Х и Y по их двумерному распределению. При этом:
H(XY)=H(X)+H(Y|X)=H(Y)+H(X|Y).
Иначе говоря, энтропия субаддитивна, аддитивность (H(XY)= H(X)+H(Y)) достигается только при полной независимости X и Y.
С помощью совместной энтропии можно написать выражение для информации IXY= IYX=I в симметричном виде:
I=H(X)+H(Y)-H(XY).
Интуитивно ясно, что включение в рассмотрение третьей переменной может лишь увеличить информацию. Это действительно так:
I(YX)Z³ IXZ, I(XY)Z³ IYZ.
Симметрия случая трех переменного описывается формулой тройной информации:
I(XY)Z+IXY=I(YZ)X+IYZ=I(XZ)Y+IXZ.
Важную роль в теории информации играет представление о максимальной скорости передачи сообщения. При этом имеется в виду скорость при которой еще возможен безошибочное получение информации на приемном конце канала связи. “Канал связи” при создании теории информации рассматривался действительно как технический канал (и задача состояла в изучении его потенциальных возможностей, тех теоретических пределов его использования, которые нельзя превзойти в принципе). В действительности “каналом связи” является любая естественная или искусственная система в которой можно выделить начальное состояние (входной сигнал) X и конечное (выходной сигнал ) Y. Законы передачи информации по каналу связи универсальны, поэтому ,например, любое физическое взаимодействие в реальных системах подчиняется не только соответствующему физическому закону, но и им также. Несмотря на сложившуюся терминологию, лучше говорить не о скорости передачи, а о скорости приема информации, которая ограничена неравенством
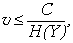
где C – пропускная способность канала (иногда ее называют также информационной емкостью, иногда емкостью называется произведение dt· C, где dt – длительность элементарного сигнала).При отсутствии шумов:
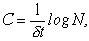
при наличии шумов:
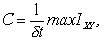
максимум отыскивается при возможном варьировании входного сигнала X. Таким образом, в общем случае:

Чем больше шумов или, на физическом языке, чем более открыта система, тем медленнее выход (конечное состояние) может воспроизвести изменения входа (начального состояния). Важную роль играет также понятие избыточности R:

Нижняя грань достигается при равномерном распределении, верхняя – при вырожденном (Xj=const). Чем больше избыточность поля, тем, очевидно, меньше скорость передачи информации. Но тем меньше вероятность ошибки при приеме! Например, чрезмерно избыточный текст скучно читать (избыток “воды”). Но малоизбыточный читать трудно, он требует крайнего внимания, в пределе (недостижимом в обычном языке) ни одну утерянную букву невозможно восстановить по смыслу. Таким образом, избыточный сигнал содержит внутренние корреляции, которые используются при восстановлении (декодировании) сообщения. Увеличивая избыточность и, соответственно, уменьшая скорость приема-передачи можно воспроизвести на выходе информацию, поданную на вход при любом уровне шумов.
Канал, для которого H(Y|X)=0 называют детерминированным, для которого H(X|Y)=0 – бесшумовым. Последний термин неудачен, поскольку зашумленной может быть не только величина X, но и Y. Канал, для которого H(Y|X)=H(X|Y)=0, называют идеальным. В идеальном канале X и Y являются взаимно – однозначными функциями. Среди нескольких теорем Шеннона особую роль в естественно- научных приложениях играет 7-я теорема, которая гласит, что в замкнутой системе энтропия при любом преобразовании не увеличивается:
H(Y)£ H(X).
На менее строгом языке это можно перефразировать так, что информацию на пути от входа к выходу можно только потерять, но не увеличить. Интуитивно это очевидно. Но если Х – начальное состояние замкнутой физической системы, а Y – конечное, то эта теорема означает необратимое уменьшение энтропии, что диаметрально противоположно общеизвестной формулировке второго начала термодинамики. Мы рассмотрим этот вопрос в п.4.
Следует отметить одну исторически обусловленную особенность приложений теории информации. С момента зарождения [11] и после наиболее мощного импульса в ее развитии приданного работами К. Шеннона [2], несмотря на общность математического аппарата и быстро замеченную ассоциированность с термодинамикой [1, 2], теория информации развивалась как раздел теории связи, Приложения быстро вышли за пределы теории связи как таковой [12]. Но и в расширенных приложениях от теории связи в неявном виде унаследовано представление об одушевленном потребителе информации. Более того, на начальном этапе авторы специально приносили своего рода извинения за то, что термин “информация” в теории имеет более широкий смысл, чем его бытовое употребление, подразумевающее некоторую ценность для потребителя. В дальнейшем оказалось, что и понятие ценности информации может быть формализовано [9].
Существует однако более общая концепция приложения понятия информации как универсальной меры физического взаимодействия. Этому посвящен ряд работ с достаточно специальным подходом, например, [13-17], наиболее общая трактовка дана Х. Хармутом [18]. Наша трактовка опирается именно на эту концепцию. Но прежде чем применить ее, необходимо подробно разобрать такое базисное понятие как энтропия, поскольку, с одной стороны возможны различные формулировки, а с другой, наоборот – одинаковые математические формы имеют разный смысл (и приводят к различным результатам) взависимости от наполнения.
1. Различные формы энтропии
Энтропия (S или H) независимо вводилась Клазиусом:
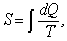 (1)
(1)
где Q – энергия, Т – температура; Л. Больцманом:
S = H = ln W, (2)
где W – вероятность состояния; К. Шенноном:
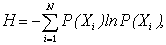 (3)
(3)
где Р – вероятность i-го уровня переменной (сигнала) Х с диапазоном изменчивости N; фон Нейманом:
H=-trr lnr, (4)
где плотность r определяется через волновую функцию y : r=|y ><y |.
Оказалось, что (1) и (3) являются следствиями (1) [1,2,10], хотя для их применения, соответственно в термодинамике и в теории информации, это не имеет большого значения. (4) является квантовомеханическим обобщением (3), при этом (4)  (3) для чистых состояний. Классический уровень предоставляет слишком широкие возможности для обобщений, чтобы затрагивать в данном обзоре и квантовый, поэтому мы не будем переходить на последний и лишь слегка коснемся удивительных особенностей квантовой энтропии в Заключении.
(3) для чистых состояний. Классический уровень предоставляет слишком широкие возможности для обобщений, чтобы затрагивать в данном обзоре и квантовый, поэтому мы не будем переходить на последний и лишь слегка коснемся удивительных особенностей квантовой энтропии в Заключении.
Можно заметить, что в отличие от (2) – (4) согласно определению (1) энтропии размерна (Дж/К). Здесь мы просто сохранили оригинальные определения. Безразмерная энтропия, конечно удобнее и, чтобы привести (1) к безразмерному виду, надо просто разделить правую часть на постоянную Больцмана k . Эта постоянная не имеет большего смысла, чем коэффициент связи между единицами измерения энергии и температуры. Если бы мы стали измерять температуру в джоулях (что неудобно, но законно), то надобность в этой константе отпала бы. Однако здесь есть чисто количественный нюанс. Величина k весьма мала: 1,38· 10-23 Дж/К. Разделив (1) на k мы сразу получаем представление о том, насколько велики изменения энтропии в самых заурядных термодинамических процессах по сравнению с теми, которыми мы оперируем в информатике. Это дает представление о том, насколько велика недоступная на макроуровне информация о микросостоянии вещества. Определение (1) – практически самое важное для теплофизике [1], но, пользуясь им, трудно увидеть универсальность понятия энтропии. Принципиальным недостатком (1) является также то, что это формула верна только для квазиравновесных состояний. Поэтому мы сосредоточимся на определениях (2) и (3).
Вероятность состояния W определяется как отношение числа микросостояний K, благоприятных данному макросостоянию, к полному числу возможных микросостояний L:
W = K/L. (5)
Пусть рассматриваются пространственные или временные вариации некоторого параметра Х (в дискретном виде). Тогда К – это число вариаций, удовлетворяющих данному распределению вероятностей P(Xi), L – полное число возможных вариаций.
Пусть М – число членов статистического ансамбля (в нашем контексте это объем, а для одномерного случая – длина ряда, выраженная числом искусственных квантов пространства, т.е. отсчетов), mi – число заполнения i-го уровня (т.е. P(Xi)=mi/M). Тогда
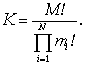 (6)
(6)
Число L однозначно определить обычно сложнее. Поэтому вместо W пользуются К (так называемая абсолютная или термодинамическая вероятность) и определяют не нормированную энтропию (2), а абсолютную На :
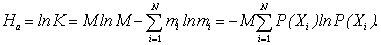 (7)
(7)
Можно показать[10], что энтропия Клазиуса (1) является частным случаем (7). Нормируя на число членов ансамбля (длину ряда), получаем абсолютную удельную энтропию
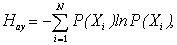 (8)
(8)
0£ Hay£ ln N, (9)
совпадающую с (3), которая была введена К.Шенноном просто как удобный функционал и была названа им “энтропия” именно из-за обнаруженного родства с термодинамической энтропией. Верхняя грань достигается при равномерном распределении, нижняя – при вырожденном (Х не зависит от координаты r: Xj = const).
Микросостояния в нашем случае различимы, следовательно ансамбль удовлетворяет статистике Максвелла-Больцмана. Роль различимой частицы в геофизической интерпретации играет квант пространства (или времени). Для этой статистики в термодинамике число L определяется как [10]:
L1=NM (10)
и соответствует в теории информации числу возможных сообщений [8]. На нашем языке это можно перефразировать как число различимых вариаций в диапазоне N при объеме (или длине ряда) М. Тогда согласно (5) нормированная удельная энтропия равна:
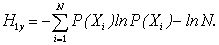 (11)
(11)
Вполне естественное для термодинамики (М – число частиц в фиксированном объеме N) и теории технического канала связи (М – длина сообщения, N – фиксированный диапазон уровней) определение l1 трудно считать адекватным в контексте естественных процессов. Здесь М может быть естественным образом ограничена, и даже искусственное ограничение не вызывает особых затруднений (подобно спектральному анализу и вообще выборочной статистике), но диапазон N трудно считать фиксированным, в особенности для естественных полей. Так при гауссовом распределении 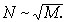
В статистике Бозе-Эйнштейна принято другое определение L [10], которое в нашем контексте может быть интерпретировано как число различимых вариаций с данным интегралом (точнее, суммой) U при объеме М:
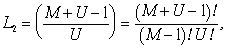 (12)
(12)
где U= 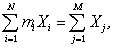 причем все Xj³ 0 (практически это легко достигается рассмотрением вместо уровней Х “энергетических” уровней Х2 ). Тогда
причем все Xj³ 0 (практически это легко достигается рассмотрением вместо уровней Х “энергетических” уровней Х2 ). Тогда
 (13)
(13)
При M>>1, U>>1 (естественное условие применения любой статистики):
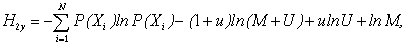 (13`)
(13`)
где u=U/M.
Таким образом, L – это , в итоге, не вообще полное число различимых вариаций (которое бесконечно), а полное число при некоторых ограничениях – при фиксированном диапазоне N или при фиксированном интеграле U, который может в ряде случаев интерпретироваться как энергия вариации. Возможны и другие варианты ограничений.
Нормированные энтропии (11) и (13) имели бы наиболее ясный физический смысл, однако в случае изучения вариаций естественных полей возникают дополнительные трудности.
Так из (9) и (11) следует
- ln N£ H1y £ 0.
Но для геофизических вариационных рядов N определяется естественно только из самой реализации. Нижняя грань соответствует Xj=const, т.е. N = 1, и оба противоположных случая равномерного и вырожденного распределений смыкаются.
Нижняя грань H2y для вырожденного распределения (Х j = const) определяется из (13`) как
inf H2y= -2 ln 2.
Заметим, что это выражение совпадает с классическим пределом энтропии квантовомеханического ансамбля, выведенным из других соображений [15].
Верхняя грань H2y соответствует, однако, не равномерному распределению, а определяется из уравнения
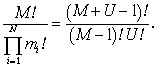
Единственное решение этого уравнения U=1 соответствует импульсной функции в вариационном ряду Xj . Для геофизического вариационного ряда естественная длина для финитной функции Xj в данном случае получается М=1. Это вырожденный случай для самого функционала энтропии. Таким образом, формальное соотношение
-2ln2 £ H2y £ 0
не имеет такого же ясного смысла как (9).
По этим причинам мы в дальнейшем в основном будем пользоваться абсолютной удельной энтропией (8), опуская для краткости нижние индексы подобно (3).
Теорема отсчетов
Теорема отсчетов является центральной темой дискретизации сигналов. Дискретизация – это получение отсчетов (sampling) сигнала. При произвольной частоте отсчетов  дискретизация является неоднозначным процессом. Из нижеследующей иллюстрации очевидно следует, что одной и той же последовательности отсчетов может соответствовать бесчисленное множество функций. Как часто, с какой частотой FS следует брать отсчеты, чтобы не допустить потери информации в сигнале? Ответ на этот вопрос дает теорема отсчетов. Чтобы её сформулировать рассмотрим более подробно процесс дискретизации в частотной области. Как показано в предыдущей лекции, спектр дискретного сигнала при частоте отсчетов
дискретизация является неоднозначным процессом. Из нижеследующей иллюстрации очевидно следует, что одной и той же последовательности отсчетов может соответствовать бесчисленное множество функций. Как часто, с какой частотой FS следует брать отсчеты, чтобы не допустить потери информации в сигнале? Ответ на этот вопрос дает теорема отсчетов. Чтобы её сформулировать рассмотрим более подробно процесс дискретизации в частотной области. Как показано в предыдущей лекции, спектр дискретного сигнала при частоте отсчетов 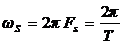 имеет вид
имеет вид 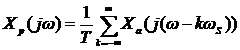 ,здесь
,здесь  - спектр аналогового сигнала (до дискретизации). Т.о., спектр дискретного сигнала Xp(jω) – периодический с периодом
- спектр аналогового сигнала (до дискретизации). Т.о., спектр дискретного сигнала Xp(jω) – периодический с периодом 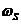 .
.
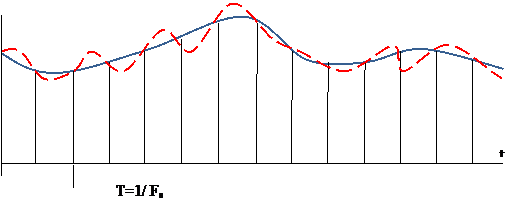
Будем рассматривать аналоговый сигнал xa(t) с ограниченной полосой частот (ограниченным или финитным спектром), при этом ωm – верхняя граничная частота спектра сигнала. Такой сигнал называют частотно – ограниченным, англ. bandlimited signal. При дискретизации таких сигналов возможны два случая.
1. Частота отсчетов  , при этом поведение спектров имеет следующий вид
, при этом поведение спектров имеет следующий вид
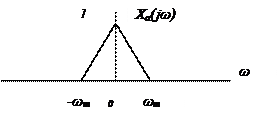
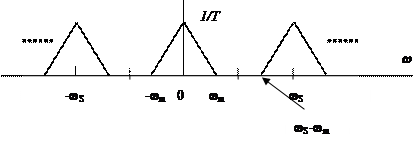

В этом случае при дискретизации не происходит наложение спектров. Поэтому если после дискретизации пропустить сигнал через фильтр нижних частот с усилением Т и частотой среза 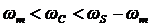 , то возможно восстановление исходного аналогового сигнала. Выходной сигнал фильтра
, то возможно восстановление исходного аналогового сигнала. Выходной сигнал фильтра 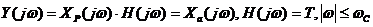
2. Частота отсчетов 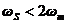 , при этом происходит наложение (aliasing) повторяющихся спектров. Спектр дискретного сигнала имеет следующий характер
, при этом происходит наложение (aliasing) повторяющихся спектров. Спектр дискретного сигнала имеет следующий характер
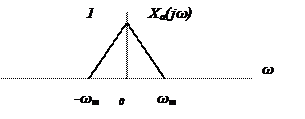

При дискретизации с частотой 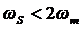 спектр аналогового сигнала Xa(jω) не может быть точно восстановлен пропусканием его через ФНЧ из-за наложения репликаций(повторений) соседних спектров. Происходит наложение (aliasing) соседних копий спектра на основную полосу частот сигнала. Таким образом, мы обосновали основной результат в дискретизации сигналов – теорему отсчетов. Если сигнал не имеет спектральных составляющих с частотами выше fm, то он полностью определяется своими отсчетами в дискретные моменты времени через интервал отсчетов
спектр аналогового сигнала Xa(jω) не может быть точно восстановлен пропусканием его через ФНЧ из-за наложения репликаций(повторений) соседних спектров. Происходит наложение (aliasing) соседних копий спектра на основную полосу частот сигнала. Таким образом, мы обосновали основной результат в дискретизации сигналов – теорему отсчетов. Если сигнал не имеет спектральных составляющих с частотами выше fm, то он полностью определяется своими отсчетами в дискретные моменты времени через интервал отсчетов 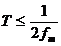 или с частотой отсчетов
или с частотой отсчетов 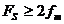 .
.
Т.о., частота отсчетов должна быть не меньше, чем 2fm. то есть при соблюдении условий теоремы отсчетов по дискретному сигналу можно восстановить исходный сигнал с финитным спектром без искажений. Ограничение теоремы имеет смысл неравенства. Минимальная частота отсчетов – это 2fm. На практике обычно используют 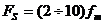 , в зависимости от требуемой точности восстановления сигнала. Например, клиническая ЭКГ имеет полосу частот 0,05 – 100 Гц, и обычно используется частота дискретизации 500 Гц.
, в зависимости от требуемой точности восстановления сигнала. Например, клиническая ЭКГ имеет полосу частот 0,05 – 100 Гц, и обычно используется частота дискретизации 500 Гц.
Теорему отсчетов называют также теоремой Найквиста, теоремой Шеннона, теоремой Котельникова. Результат получен независимо этими тремя авторами в конце 20-х и в начале тридцатых годов ХХ века.
Частота  [рад/с] или FS [Гц] - это частота (скорость) отсчетов. Частота
[рад/с] или FS [Гц] - это частота (скорость) отсчетов. Частота 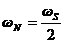 или
или 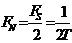 называется частотой Найквиста (частотой Котельникова) или частотой свертывания (folding frequency). При определенной частоте отсчетов FS она определяет максимальную граничную частоту сигнала fm . Необходимое условие дискретизации
называется частотой Найквиста (частотой Котельникова) или частотой свертывания (folding frequency). При определенной частоте отсчетов FS она определяет максимальную граничную частоту сигнала fm . Необходимое условие дискретизации 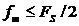 .
.
Наложение (алиасинг, англ. aliasing) гармоник при дискретизации сигналов.Рассмотрим вновь связь аналоговой синусоиды  и дискретной
и дискретной
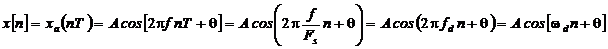 Здесь f –частота аналоговой гармоники,
Здесь f –частота аналоговой гармоники, 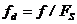 – дискретная частота гармоники, FS – частота отсчетов, Т - интервал отсчетов. Для дискретной синусоиды частота
– дискретная частота гармоники, FS – частота отсчетов, Т - интервал отсчетов. Для дискретной синусоиды частота  - это нормализованная частота, т.е. частота аналогового сигнала, деленная на частоту отсчетов FS,
- это нормализованная частота, т.е. частота аналогового сигнала, деленная на частоту отсчетов FS, 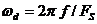 - угловая (круговая) нормализованная частота.
- угловая (круговая) нормализованная частота.
При одинаковых значениях f / FS получаем одно и то же значение x[n].
По теореме отсчетов необходимо, чтобы 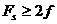 или
или 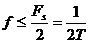 . Таким образом, при частоте отсчетов Fs максимально возможная частота синусоиды
. Таким образом, при частоте отсчетов Fs максимально возможная частота синусоиды  . Если это условие не выполняется, то возникает алиасинг (наложение гармоник).
. Если это условие не выполняется, то возникает алиасинг (наложение гармоник).
Например, если частота отсчетов Fs = 40 Гц и частота одной гармоники f1 = 10 Гц, а другой f2 = 50 Гц, то  .
.
Представим эти дискретные гармоники при дискретизации с частотой 40 Гц

Отсюда видно, что 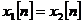 , т.е. при такой частоте дискретизации гармоники с частотами 10 Гц и 50 Гц не различимы. Произошло наложение (aliasing) гармоник. Демонстрация примера в Matlab:
, т.е. при такой частоте дискретизации гармоники с частотами 10 Гц и 50 Гц не различимы. Произошло наложение (aliasing) гармоник. Демонстрация примера в Matlab:
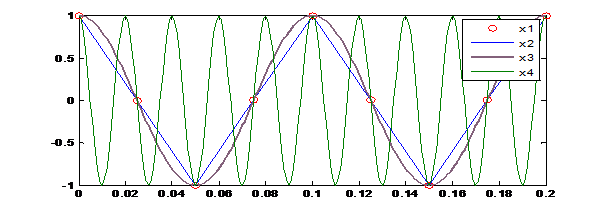
f=40; t=0:1/f:0.2; x1=cos(2*pi*10*t); x2=cos(2*pi*50*t); plot(t,x1,'ro',t,x2)
t1=0:0.001:0.2; hold on x3=cos(2*pi*10*t1); x4=cos(2*pi*50*t1); plot(t1,x3,t1,x4)
legend('x1', 'x2', 'x3', 'x4')
Сигналы x1, x2 дискретизированы с частотой f = 40 Гц, сигналы x3, x4 – с частотой 1000 Гц.
Частота Найквиста 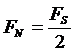 , называемая также частотой свертывания (folding frequency), является также частотой, относительно которой происходит свертывание по частоте гармоник более высоких частот.
, называемая также частотой свертывания (folding frequency), является также частотой, относительно которой происходит свертывание по частоте гармоник более высоких частот.
Диаграмма, поясняющая свертывание гармоник
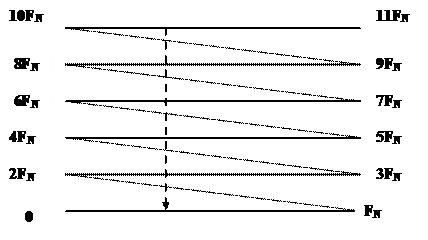
Все гармоники с частотами 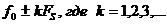 в результате дискретизации налагаются друг на друга (подменяют друг друга). Например, для вышеприведенного примера гармоники с частотой f1= 10 Гц и f2=10+1* 40 = 50 Гц при дискретизации с частотой 40 Гц неразличимы. Частоты
в результате дискретизации налагаются друг на друга (подменяют друг друга). Например, для вышеприведенного примера гармоники с частотой f1= 10 Гц и f2=10+1* 40 = 50 Гц при дискретизации с частотой 40 Гц неразличимы. Частоты 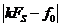 могут образовывать ложные частотные компоненты.
могут образовывать ложные частотные компоненты.
Другой пример алиасинга. Гармоника с частотой 10+1*44,1=54,1 кГц для уха человека – неслышимая. Но помеха с такой частотой, появившаяся от внешнего источника, например, искрящего контактного провода или атмосферного разряда, при дискретизации с частотой 44,1 кГц будет трансформирована в слышимую частоту 10 кГц (10+1*44,1=54,1), если аналоговый сигнал до АЦП предварительно не отфильтрован.
Неправильная дискретизация аналогового сигнала приводит к тому, что высокочастотные составляющие накладываются на низкочастотные, в результате чего восстановление сигнала во времени сопровождается его искажением. В частности, при съемке камерой быстро вращающихся объектов алиасинг может привести к эффекту, когда изображение объекта замедляет вращение или вращается в обратную сторону.
Диаграмма, поясняющая свертывание гармоник
Частота 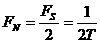 - это частота Найквиста. Можно представлять, что ось частот f над интервалом 0 – FNсложена гармошкой отрезками по FN Гц. Поэтому частота Найквиста называется такжечастотой свертывания.
- это частота Найквиста. Можно представлять, что ось частот f над интервалом 0 – FNсложена гармошкой отрезками по FN Гц. Поэтому частота Найквиста называется такжечастотой свертывания.

Все гармоники с частотами 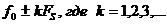 в результате дискретизации налагаются друг на друга (подменяют друг друга). Например, для вышеприведенного примера гармоники с частотой f1= 10 Гц и f2=10+1* 40 = 50 Гц при дискретизации с частотой 40 Гц неразличимы. Частоты
в результате дискретизации налагаются друг на друга (подменяют друг друга). Например, для вышеприведенного примера гармоники с частотой f1= 10 Гц и f2=10+1* 40 = 50 Гц при дискретизации с частотой 40 Гц неразличимы. Частоты 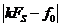 могут образовывать ложные частотные компоненты.
могут образовывать ложные частотные компоненты.
Другой пример алиасинга. Гармоника с частотой 10+1*44,1=54,1 кГц для уха человека – неслышимая. Но помеха с такой частотой, появившаяся от внешнего источника, например, искрящего контактного провода или атмосферного разряда, при дискретизации с частотой 44,1 кГц будет трансформирована в слышимую частоту 10 кГц (10+1*44,1=54,1), если аналоговый сигнал до АЦП предварительно не отфильтрован.
Неправильная дискретизация аналогового сигнала приводит к тому, что высокочастотные составляющие накладываются на низкочастотные, в результате чего восстановление сигнала во времени сопровождается его искажением. В частности, при съемке камерой быстро вращающихся объектов алиасинг может привести к эффекту, когда изображение объекта замедляет вращение или вращается в обратную сторону.
Фильтры защиты от наложений спектров. Из соотношения неопределенности для сигналов
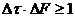
следует, что сигналы конечной длительности 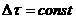 теоретически не могут иметь конечную ширину спектра, поскольку ширина полосы сигнала
теоретически не могут иметь конечную ширину спектра, поскольку ширина полосы сигнала 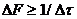 . Поэтому при дискретизации реальных сигналов конечной длительности всегда происходит наложение спектров. Вид спектра после дискретизации для аналоговых сигналов с неограниченным спектром. «Хвосты» спектров продолжаются по всей оси частот
. Поэтому при дискретизации реальных сигналов конечной длительности всегда происходит наложение спектров. Вид спектра после дискретизации для аналоговых сигналов с неограниченным спектром. «Хвосты» спектров продолжаются по всей оси частот  .
.
Очевидно, что в большей или меньшей мере возникает наложение спектров. В результате искажается спектр основной полосы сигнала, а значит, и сам сигнал. Для устранения или по крайней мере для значительного уменьшения влияния наложения спектров при аналого – цифровом преобразовании (АЦП) сигналов используют фильтры защиты от наложений спектров. Их называют также предфильтрами или антиалиасинговыми фильтрами (antialising filter). Такой фильтр должен резко ослаблять частотные составляющие спектра сигнала с частотами выше частоты Найквиста 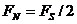 .
.

Фильтр защиты от наложений должен подавлять составляющие частотного спектра сигнала на частотах, превышающих частоту Найквиста до уровня, меньшего, чем погрешность (шум) квантования,
Отсюда минимальное ослабление фильтра на частоте Найквиста должно быть не менее 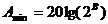 дБ. Здесь В – число бит АЦП, 2В - число уровней квантования.
дБ. Здесь В – число бит АЦП, 2В - число уровней квантования.
Например, для 10-битового АЦП 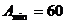 дБ, для 16 –битового АЦП
дБ, для 16 –битового АЦП 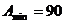 дБ.
дБ.
В относительных единицах 60 дБ составляет 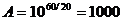 , а 90 дБ -
, а 90 дБ - 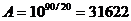 . Т.е. коэффициент передачи фильтра в полосе задерживания должен быть более чем в 30000 раз меньше, чем в полосе пропускания.
. Т.е. коэффициент передачи фильтра в полосе задерживания должен быть более чем в 30000 раз меньше, чем в полосе пропускания.
Таким образом, к низкочастотным фильтрам защиты от наложений спектров предъявляются высокие требования по необходимому ослаблению в переходной полосе и полосе задерживания, а также ширины переходной полосы. Такие аналоговые фильтры являются достаточно сложными и дорогими и удорожают стоимость аппаратуры. Альтернатива: увеличение частоты отсчетов FS значительно выше 2fm (oversampling).
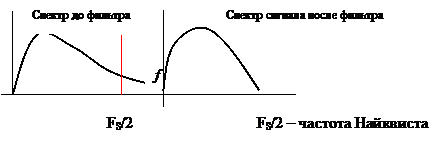
Дата добавления: 2015-12-26; просмотров: 4628;
