Матричное кодирование

Ранее каждая схема кодирования описывалась таблицами, задающими кодовое слово длины 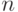для каждого исходного слова длины 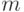. Для блоков большой длины этот способ требует большого объема памяти и поэтому непрактичен. Например, для 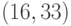-кода потребуется 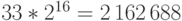бит.

Гораздо меньшего объема памяти требует матричное кодирование. Пусть матрица размерности , состоящая из элементов 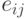, где 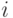- это номер строки, а 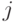- номер столбца. Каждый из элементов матрицы 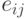может быть либо 0, либо 1. Кодирование реализуется операцией или , где кодовые слова рассматриваются как векторы, т.е как матрицы-строки размера .

Пример. Рассмотрим следующую -матрицу:

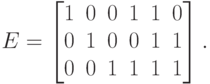
Тогда кодирование задается такими отображениями: , , , , , , , .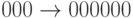

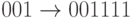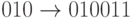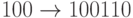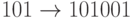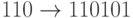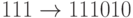Рассмотренный пример показывает преимущества матричного кодирования: достаточно запомнить 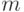кодовых слов вместо 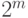слов. Это общий факт.

Кодирование не должно приписывать одно и то же кодовое слово разным исходным сообщениям. Простой способ добиться этого состоит в том, чтобы 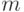столбцов (в предыдущем примере - первых) матрицы образовывали единичную матрицу. При умножении любого вектора на единичную матрицу получается этот же самый вектор, следовательно, разным векторам-сообщениям будут соответствовать разные вектора систематического кода.

Матричные коды называют также линейными кодами. Для линейных 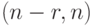-кодов с минимальным расстоянием Хэмминга существует нижняя граница Плоткина (Plotkin)³ для минимального количества контрольных разрядов при ,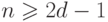

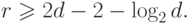
Упражнение 39. Вычислить минимальную оценку по Плоткину количества дополнительных разрядов для кодовых слов матричного кода, если требуется, чтобы минимальное расстояние между ними было . Рассмотреть случаи из предыдущего упражнения.