Тема 2.1. Теорема отчетов

ИНФОРМАЦИЯ И ЭНТРОПИЯ.

	Клоду Шеннону удалось придумать удивительно простую и глубокую модель передачи информации, без которой теперь не обходится ни один учебник. Он ввел понятия: источник сообщения, передатчик, канал связи, приемник, получатель сообщения и источник шума, который может исказить сигнал. Практически любой, даже очень сложный, обмен сообщениями можно успешно описать в этих терминах.

Дискретное сообщение — это любой набор символов, который формируется Источником (им может быть, например, человек). От Источника сообщение переходит к Передатчику, который преобразует его к виду, который уже можно передавать по Каналу связи. Например, Передатчик может кодировать сообщение. Преобразованное сообщение называется Сигналом. Канал связи — это технический комплекс аппаратуры, который позволяет передать Сигнал. В общем случае в процессе передачи сигнал в канале искажается шумом, который исходит от Источника шума. Приемник обычно выполняет операцию, обратную по отношению к той, что производится передатчиком, — т. е. восстанавливает сообщение по сигналам. Процесс преобразования сигнала в сообщения, осуществляемый в Приемнике, называют декодированием. Получатель — это человек или аппарат, для которого предназначено сообщение.

Энтропия

В 1946 г. американский ученый-статистик Джон Тьюки предложил название БИТ (BIT — аббревиатура от BInary digiT), одно из главных понятий XX века. Тьюки избрал бит для обозначения одного двоичного разряда, способного принимать значение 0 или 1. Шеннон использовал бит как единицу измерения информации. Мерой количества информации Шеннон предложил считать функцию, названную им энтропией.

Пусть сообщение — осмысленное предложение на русском языке. Шеннон заметил, что при передаче различных букв мы передаем разное количество информации. Если мы передаем часто встречающиеся буквы, то информация меньше; при передаче редких букв — больше. Это видно при кодировании букв алфавита азбукой Морзе. Наиболее частые буквы передаются коротко, а для редких используют более длинные цепочки. Так, буква «Е» кодируется одной точкой «.», а редкая «Ш» — четырьмя тире «––––» (это самая длинная последовательность на букву в азбуке Морзе).

Количество информации на букву связано с частотой употреблений этой буквы во всех сообщениях, формируемых на языке. Чем более редкую букву мы передаем, тем больше в ней информации.
Энтропия — мера непредсказуемости. Это понятие Шеннон взял из статистической термодинамики. Пусть вероятность i-того символа алфавита, состоящего из n символов (мера частоты, с которой встречается символ во всех сообщениях языка), равна pi. Тогда информация одного символа:

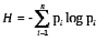
(здесь log — логарифм по основанию 2).
Шеннон пишет: «Величина H играет центральную роль в теории информации в качестве меры количества информации, возможности выбора и неопределенности». Количество информации, передаваемое в сообщении, тесно связано с мерой неопределенности, или непредсказуемости передаваемых символов.

Избыточность

Пусть источник сообщения передает предложение реального языка. Оказывается, каждый следующий символ не полностью случаен, и вероятность его появления не полностью предопределена средней частотой символа во всех сообщениях языка. То, какой символ последует дальше, зависит от символов, уже переданных. Например, в русском языке после символа «Ъ» не может идти символ согласного звука. После двух подряд гласных «Е» третий гласный «Е» следует крайне редко (например, в слове «длинношеее»). Таким образом, каждый следующий символ в некоторой степени предопределен, поэтому можно говорить об условной энтропии символа.

Источник может порождать сообщения строго определенного типа — например, формальную деловую переписку; в таком случае предопределенность следующего символа может быть намного выше, чем в среднем в языке. Тогда энтропия этого источника будет отличаться от максимальной: она будет меньше. Если мы сравним энтропию конкретного источника и максимальную энтропию, то определим избыточность сообщения.

Избыточность обычного английского текста составляет примерно 50%. Это значит, что когда мы пишем по-английски, то половина знаков предопределяется структурой языка и лишь половина выбирается свободно. То есть избыточность — это мера предсказуемости сообщения. Понятия энтропии (непредсказуемости) сообщения и избыточности (предсказуемости) естественно соответствуют интуитивным представлениям о мере информации. Чем более непредсказуемо сообщение (и чем больше его энтропия, потому что меньше вероятность) — тем больше информации оно несет.

Сенсация — это редкое событие, предсказуемость которого очень мала, и потому велика его информационная стоимость. Часто информацией называют новости — сообщения о только что произошедших событиях, о которых мы еще не знаем. Но если о случившемся нам расскажут во второй и третий раз, избыточность сообщения станет очень велика, его непредсказуемость упадет до нуля, и мы просто не станем слушать, отмахиваясь от говорящего со словами: «Знаю, знаю». Поэтому-то средства массовой информации (СМИ) и стараются быть первыми. Вот это соответствие интуитивному чувству новизны, которое рождается неожиданным известием, и сыграло главную роль в том, что статья Шеннона, не рассчитанная на массового читателя, стала сенсацией, которую подхватила пресса и которую приняли как универсальный ключ к познанию природы ученые самых разных специальностей — от лингвистов и литературоведов до биологов.
Но понятие информации, по Шеннону, — это строгая математическая теория, и ее применение за пределами теории связи очень рискованно. Зато в самой теории связи она играет центральную роль.

Тема 2.1. Теорема отчетов