Модель Эрроу-Дебре. Существование конкурентного равновесия
Структурно модель Эрроу-Дебре весьма близка к модели Вальраса. От последней она отличается конкретизацией природы происхождения функций предложения и спроса, а также механизма образования дохода потребителя.
Для каждого производителя j введем множество 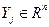 , которое, в отличие от модели Вальраса, здесь будем трактовать как множество производственных планов (а не оптимальных планов), т.е. это есть множество
, которое, в отличие от модели Вальраса, здесь будем трактовать как множество производственных планов (а не оптимальных планов), т.е. это есть множество  - мерных векторов
- мерных векторов 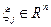 , часть компонент которых описывает затраты, а другая часть - соответствующие этим затратам выпуски товаров. Компоненты, соответствующие затратам, как и в модели Вальраса, снабжаются отрицательными знаками. Поэтому скалярное произведение
, часть компонент которых описывает затраты, а другая часть - соответствующие этим затратам выпуски товаров. Компоненты, соответствующие затратам, как и в модели Вальраса, снабжаются отрицательными знаками. Поэтому скалярное произведение 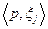 показывает прибыль, полученную производителем j в результате реализации плана
показывает прибыль, полученную производителем j в результате реализации плана 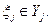 Отсюда оптимальный план
Отсюда оптимальный план 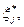 участвующий в определении совокупного предложения (см. (4.3.4) и (4.3.10)), определяется как решение задачи:
участвующий в определении совокупного предложения (см. (4.3.4) и (4.3.10)), определяется как решение задачи:
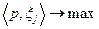 при ограничениях
при ограничениях 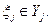 (4.4.1)
(4.4.1)
Оптимальное решение этой задачи обозначим через 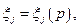 а множество всех таких решений (множество оптимальных планов) - через
а множество всех таких решений (множество оптимальных планов) - через 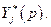 Если задача (4.4.1) имеет единственное решение, то
Если задача (4.4.1) имеет единственное решение, то 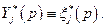
Доход потребителя i складывается следующим образом. Вводится коэффициент 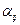 , который показывает долю i-го потребителя в прибыли j-го производителя. Предполагается (как и в модели Вальраса), что прибыль каждого производителя делится между всеми потребителями полностью, т.е. для любого
, который показывает долю i-го потребителя в прибыли j-го производителя. Предполагается (как и в модели Вальраса), что прибыль каждого производителя делится между всеми потребителями полностью, т.е. для любого 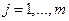
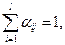
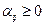 .
.
Пользуясь коэффициентами 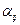 , суммарные дивиденды
, суммарные дивиденды 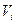 , получаемые потребителем i от производственного сектора, можно представить в виде
, получаемые потребителем i от производственного сектора, можно представить в виде
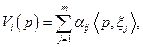
где 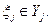 Поэтому общий доход потребителя i при реализации производственных планов
Поэтому общий доход потребителя i при реализации производственных планов  вычисляется по формуле
вычисляется по формуле
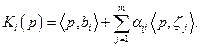
Функция спроса потребителя конкретизируется следующим образом. Вводится множество допустимых векторов потребления 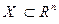 , а предпочтение потребителя на этом множестве задается с помощью функции полезности
, а предпочтение потребителя на этом множестве задается с помощью функции полезности 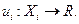 В результате вектор-функция спроса, строится как решение задачи:
В результате вектор-функция спроса, строится как решение задачи:
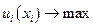
при ограничениях (4.4.2)
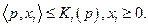
Оптимальное решение этой задачи обозначим через 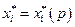 , а множество всех таких решений – через
, а множество всех таких решений – через 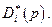 Если задача (4.4.2) имеет единственное решение, то
Если задача (4.4.2) имеет единственное решение, то
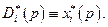
Таким образом, очерчены конкретные виды множеств в правых частях соотношений (4.3.3) и (4.3.4) , определяющих функции совокупных спроса и предложения:
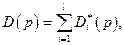 (4.4.3)
(4.4.3)
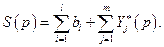 (4.4.4)
(4.4.4)
Модель (4.3.5) , в которой функции и определены в виде (4.4.3) и (4.4.4) , называется моделью Эрроу-Дебре, если выполнены следующие требования.
У-1. Множество 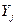 компактно в
компактно в 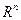 и содержит нулевой вектор
и содержит нулевой вектор 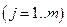 .
.
У-2. Множество 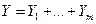 выпукло в
выпукло в 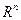 .
.
У-3. Множество 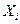 замкнуто и выпукло в
замкнуто и выпукло в 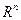 и таково, что из
и таково, что из 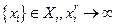 для некоторого r , следует
для некоторого r , следует 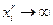 для всех
для всех 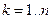
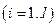 .
.
У-4. Функция полезности 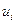 непрерывно дифференцируема на
непрерывно дифференцируема на 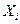 и строго вогнута
и строго вогнута 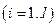 .
.
У-5. Функция 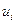 обладает свойством ненасыщаемости
обладает свойством ненасыщаемости 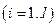 .
.
У-6. Существует 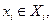 для которого
для которого 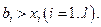
Условие У-1, с учетом непрерывности функции прибыли, обеспечивает существование решения задачи (4.4.2) . Условие У-2 допускает эффективность использования «смешанных» планов производства на уровне всего производственного сектора. Условия У-3 и У-4 имеют технический характер (определение вогнутости и ненасыщаемости функции полезности и их содержательная трактовка были приведены в разделе 2.2). Условие У-6 требует наличия у каждого потребителя «существенного» начального запаса всех товаров. Оно считается достаточно жестким, но без него (или незначительного его ослабления) нельзя доказать существование конкурентного равновесия в модели Эрроу-Дебре (см. замечание после доказательства теоремы 5.2).
Эта одна из первых теорем существования была доказана авторами рассматриваемой модели в 1954 году, спустя несколько десятилетий после создания модели Вальраса.
Пусть 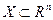 , а F - множественнозначное отображение, которое переводит каждую точку
, а F - множественнозначное отображение, которое переводит каждую точку 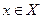 в некоторое подмножество множества X
в некоторое подмножество множества X 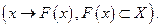
Отображение F называется полунепрерывным сверху, если из соотношений 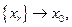 где
где 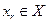 и
и 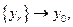 где
где 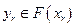 , следует
, следует 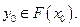 Другими словами, для каждого открытого множества U , содержащего множество
Другими словами, для каждого открытого множества U , содержащего множество 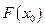 , можно найти такое число
, можно найти такое число 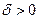 , что
, что 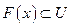 , как только
, как только 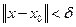 (где
(где 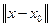 - расстояние между точками
- расстояние между точками 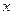 и
и 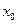 ).
).
Непрерывное отображение всегда полунепрерывно сверху, а обратное неверно. Чтобы полунепрерывное сверху отображение было непрерывным, нужно, чтобы оно было одновременно полунепрерывным снизу, т.е. для каждого 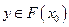 при
при 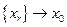 существовали такие
существовали такие 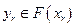 , что
, что 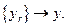
Отображение F называется ограниченным, если для любого 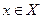 множество
множество 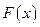 является ограниченным, как подмножество евклидова пространства
является ограниченным, как подмножество евклидова пространства 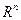 .
.
Лемма 5.1. Пусть P , X - выпуклые и компактные подмножества пространства 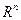 ,
, 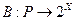 - такое множественнозначное отображение, что для любого
- такое множественнозначное отображение, что для любого 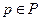 множество
множество 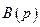 есть непустой выпуклый компакт. Тогда множественнозначное отображение
есть непустой выпуклый компакт. Тогда множественнозначное отображение 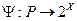 , такое, что
, такое, что
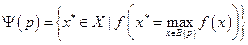
полунепрерывно сверху, если функция 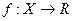 непрерывна и вогнута.
непрерывна и вогнута.
Пусть 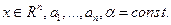 Линейное уравнение
Линейное уравнение 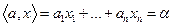 называется гиперплоскостью в
называется гиперплоскостью в 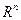 (или
(или 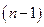 -мерным линейным многообразием). Это есть обобщение понятия обычной плоскости в
-мерным линейным многообразием). Это есть обобщение понятия обычной плоскости в 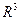 . Гиперплоскость
. Гиперплоскость 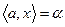 делит все пространство
делит все пространство 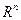 на две части:
на две части: 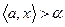 и
и 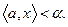
Пусть 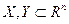 . Говорят, что гиперплоскость
. Говорят, что гиперплоскость 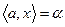 разделяет X и Y , если для всех
разделяет X и Y , если для всех 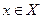
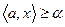 , а для всех
, а для всех 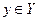
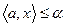 . Например, если X и Y - выпуклые множества, не имеющие общих точек, то, очевидно, между ними существует разделяющая гиперплоскость.
. Например, если X и Y - выпуклые множества, не имеющие общих точек, то, очевидно, между ними существует разделяющая гиперплоскость.
Лемма 5.2. Пусть 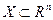 - выпуклое множество, не имеющее общих точек с неотрицательным ортантом
- выпуклое множество, не имеющее общих точек с неотрицательным ортантом 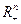 . Тогда найдется вектор
. Тогда найдется вектор 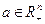 , у которого хотя бы одна компонента строго положительна и
, у которого хотя бы одна компонента строго положительна и 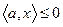 для всех (Рис. 4.7).
для всех (Рис. 4.7).
Точка 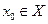 называется неподвижной точкой множественнозначного отображения F, определенного на X , если
называется неподвижной точкой множественнозначного отображения F, определенного на X , если 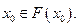
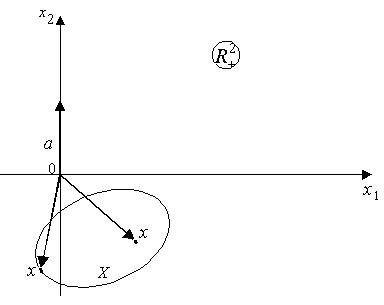
Рис. 4.7 Иллюстрация к лемме 5.2
Приведем без доказательства теорему существования неподвижной точки.
Теорема (Какутани). Пусть 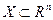 - компактное, выпуклое множество, а F - полунепрерывное сверху отображение, которое каждой точке
- компактное, выпуклое множество, а F - полунепрерывное сверху отображение, которое каждой точке 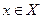 ставит в соответствие замкнутое, выпуклое подмножество
ставит в соответствие замкнутое, выпуклое подмножество 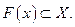 Тогда отображение F имеет неподвижную точку в X.
Тогда отображение F имеет неподвижную точку в X.
Доказательство существования равновесия в модели Эрроу-Дебре проведем с помощью леммы Гейла, которую сформулируем в терминах элементов рынка (4.3.5). Сначала пронормируем цены, поделив все 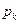 на одну и ту же величину
на одну и ту же величину 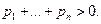 Тогда пространство цен P превращается в стандартный симплекс, лежащий в неотрицательном ортанте
Тогда пространство цен P превращается в стандартный симплекс, лежащий в неотрицательном ортанте 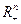 :
:
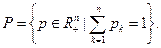
Пронормировав таким образом цены, мы не изменяем существа дела, а переходим к другому масштабу цен. В данном случае преобразование пространства цен в стандартный симплекс преследует чисто технические цели.
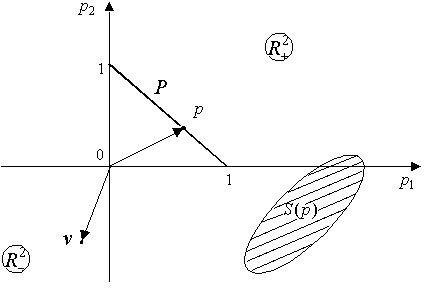
Рис. 4.8 Иллюстрация к лемме Гейла
Лемма (Гейла). Пусть S - ограниченное, полунепрерывное сверху множественнозначное отображение симплекса P в 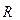 , удовлетворяющее условиям:
, удовлетворяющее условиям:
a) 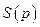 есть непустое выпуклое множество для всех
есть непустое выпуклое множество для всех 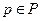 ;
;
b) для всех 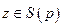
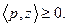 Тогда существуют такие
Тогда существуют такие 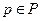 и
и 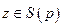 , что
, что 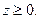
Условие b) означает, что для каждого 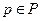 множество
множество 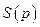 не имеет общих точек с неположительным ортантом
не имеет общих точек с неположительным ортантом 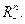 Действительно, для любой точки
Действительно, для любой точки 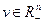 и любого
и любого 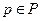
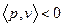 (Рис. 4.8). При этих условиях лемма Гейла утверждает о существовании такого
(Рис. 4.8). При этих условиях лемма Гейла утверждает о существовании такого 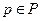 , что
, что 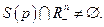
Доказательство проведем от противного: пусть лемма не верна. Это означает, что ни для одного вектора 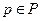 множество
множество 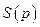 не имеет общих точек с
не имеет общих точек с 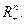 Покажем, что в этом случае существует такое сколь угодно малое положительное число
Покажем, что в этом случае существует такое сколь угодно малое положительное число 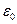 (не зависящее от
(не зависящее от 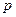 и
и 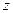 ), что семейство
), что семейство 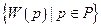 выпуклых множеств
выпуклых множеств 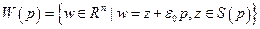 также не касается неотрицательного ортанта
также не касается неотрицательного ортанта 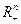 (Рис. 4.9).
(Рис. 4.9).
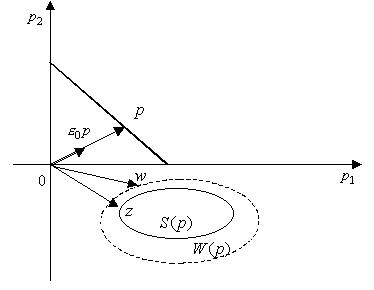
Рис. 4.9. Иллюстрация к доказательству леммы
Действительно, если бы это было так, то существовала бы последовательность 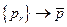 и точки
и точки 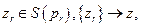 для которых
для которых 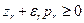 при
при 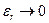 (сходящаяся последовательность
(сходящаяся последовательность 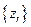 найдется, так как
найдется, так как 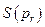 компактны и лежат в ограниченной области пространства
компактны и лежат в ограниченной области пространства 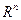 ). Тогда из полунепрерывности сверху отображения S следуют соотношения
). Тогда из полунепрерывности сверху отображения S следуют соотношения 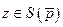 и
и 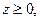 что противоречит нашему предположению. Следовательно, семейство
что противоречит нашему предположению. Следовательно, семейство 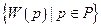 не пересекается с неотрицательным ортантом.
не пересекается с неотрицательным ортантом.
Тогда для каждого множества 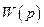 из этого семейства и положительного ортанта существует разделяющая гиперплоскость
из этого семейства и положительного ортанта существует разделяющая гиперплоскость 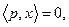 такая, что для любого
такая, что для любого 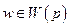
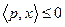 (см. лемму 5.2).
(см. лемму 5.2).
Построим множественнозначное отображение 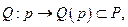 где множество
где множество 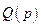 состоит из всех тех векторов симплекса P, которые представляют гиперплоскости, разделяющие положительный ортант и множество
состоит из всех тех векторов симплекса P, которые представляют гиперплоскости, разделяющие положительный ортант и множество 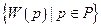 . Так как это семейство не касается с положительным ортантом, множество
. Так как это семейство не касается с положительным ортантом, множество 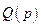 непусто (см. лемму 5.2). Отображение Q полунепрерывно сверху, как и отображение W (полунепрерывность последнего вытекает из его вида и аналогичного свойства S). В силу этого свойства отображения Q , множество
непусто (см. лемму 5.2). Отображение Q полунепрерывно сверху, как и отображение W (полунепрерывность последнего вытекает из его вида и аналогичного свойства S). В силу этого свойства отображения Q , множество 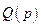 выпукло и замкнуто, как и симплекс P . Следовательно, отображение Q удовлетворяет всем условиям теоремы Какутани и потому имеет в P неподвижную точку
выпукло и замкнуто, как и симплекс P . Следовательно, отображение Q удовлетворяет всем условиям теоремы Какутани и потому имеет в P неподвижную точку 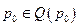 . Но, согласно условию b) леммы, для этой точки справедливо неравенство
. Но, согласно условию b) леммы, для этой точки справедливо неравенство 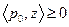 при
при 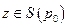 . Тогда
. Тогда 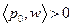 для
для 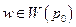 . Последнее противоречит неподвижности точки p0 в
. Последнее противоречит неподвижности точки p0 в 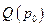 . Следовательно, наше первоначальное предположение приводит к противоречию, что и доказывает лемму.
. Следовательно, наше первоначальное предположение приводит к противоречию, что и доказывает лемму.
Теорема 4.2. В модели Эрроу-Дебре существует конкурентное равновесие.
Доказательство. Обозначим для каждого 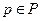
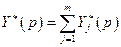
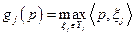 (4.4.5)
(4.4.5)
(см. (4.4.1)). Как следует из условий У-1 и У-5, множество 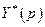 есть непустое, компактное и выпуклое множество. Обозначим через
есть непустое, компактное и выпуклое множество. Обозначим через 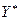 отображение
отображение 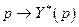 . Из непрерывности (линейности) функций
. Из непрерывности (линейности) функций 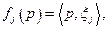
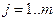 и из леммы 5.1 следует, что
и из леммы 5.1 следует, что 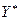 есть ограниченное, полунепрерывное сверху отображение.
есть ограниченное, полунепрерывное сверху отображение.
Так как 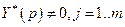 , то задача (4.4.2) должна решаться при ограничении
, то задача (4.4.2) должна решаться при ограничении
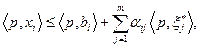 (4.4.6)
(4.4.6)
где 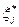 - оптимальное решение задачи (4.4.1). Известно, что для оптимального решения задачи (4.4.2) в (4.4.6) должно иметь место строгое равенство:
- оптимальное решение задачи (4.4.1). Известно, что для оптимального решения задачи (4.4.2) в (4.4.6) должно иметь место строгое равенство:
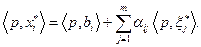 (4.4.7)
(4.4.7)
Если это неверно, то в силу условия У-5 существует 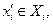 для которого
для которого 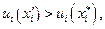 а по условию У-4 можно найти такое
а по условию У-4 можно найти такое 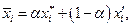 где
где 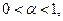 что
что 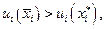 причем
причем 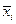 удовлетворяет ограничениям (4.4.6). Но это противоречит определению
удовлетворяет ограничениям (4.4.6). Но это противоречит определению 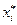 как точки максимума. Таким образом, равенство (4.4.7) действительно имеет место.
как точки максимума. Таким образом, равенство (4.4.7) действительно имеет место.
Так как по условию У-1 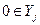 , то по определению максимума
, то по определению максимума 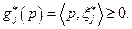 Отсюда и из условий У-1 - У-6 следует, что множество
Отсюда и из условий У-1 - У-6 следует, что множество 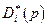 оптимальных решений задачи (4.4.2) при ограничениях (4.4.6) представляет собой непустой выпуклый компакт. Поэтому множество
оптимальных решений задачи (4.4.2) при ограничениях (4.4.6) представляет собой непустой выпуклый компакт. Поэтому множество 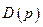 (см. (4.4.3)) также будет непустым выпуклым компактом. Из условий У-4 - У-6 и леммы 4.1 следует, что D есть полунепрерывное сверху множественнозначное отображение.
(см. (4.4.3)) также будет непустым выпуклым компактом. Из условий У-4 - У-6 и леммы 4.1 следует, что D есть полунепрерывное сверху множественнозначное отображение.
Построим отображение S для любого 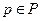 следующим образом:
следующим образом:
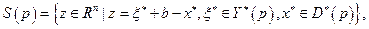 (4.4.8)
(4.4.8)
где
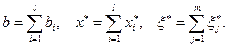
Можно показать, что S есть ограниченное, полунепрерывное сверху множественнозначное отображение из P в 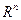 и что множество
и что множество 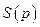 непусто, выпукло и замкнуто. Суммируя обе стороны равенства (4.4.7) по
непусто, выпукло и замкнуто. Суммируя обе стороны равенства (4.4.7) по 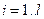 , получаем
, получаем
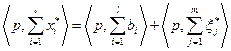
или
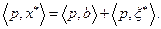
В обозначениях элементов множества 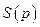 это равенство записывается в виде
это равенство записывается в виде
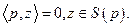 (4.4.9)
(4.4.9)
Следовательно, отображение S , порождающее для каждого 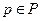 множество (4.4.8), удовлетворяет всем условиям леммы Гейла. Из этой леммы следует существование таких
множество (4.4.8), удовлетворяет всем условиям леммы Гейла. Из этой леммы следует существование таких 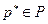 и
и 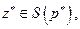 что
что 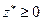 . Поэтому набор векторов
. Поэтому набор векторов 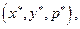 где
где 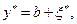 образует конкурентное равновесие в модели Эрроу-Дебре. Действительно, условие (4.3.6) выполнено по построению векторов
образует конкурентное равновесие в модели Эрроу-Дебре. Действительно, условие (4.3.6) выполнено по построению векторов 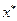 и
и 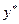 ; условие (4.3.7) следует из неравенства
; условие (4.3.7) следует из неравенства 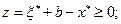 условие (4.3.8) вытекает из (4.4.9) и, наконец, отображения D и S являются функциями совокупных спроса и предложения в модели Эрроу-Дебре, так как они определены посредством соотношений (4.4.3) и (4.4.4). Теорема доказана.
условие (4.3.8) вытекает из (4.4.9) и, наконец, отображения D и S являются функциями совокупных спроса и предложения в модели Эрроу-Дебре, так как они определены посредством соотношений (4.4.3) и (4.4.4). Теорема доказана.
В связи с тем, что наиболее жестким из всех условий, определяющих модель Эрроу-Дебре, является условие У-6, рассмотрим одну возможность его ослабления.
Это условие в теореме 4.2 вместе с У-3, У-4 и леммой 4.1 обеспечивает непустоту бюджетных множеств 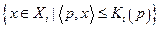 потребителей и полунепрерывность сверху функций их спроса
потребителей и полунепрерывность сверху функций их спроса 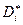 . Эти свойства не изменятся, если условие У-6 заменить следующими условиями:
. Эти свойства не изменятся, если условие У-6 заменить следующими условиями: 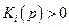 для любого вектора
для любого вектора 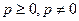 и
и 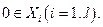 Так как второе из условий не является жестким, то существование конкурентного равновесия, помимо условий У-1 - У-5, зависит от наличия положительного дохода у всех потребителей. Очевидно, что это условие слабее, чем У-6, так как положительный доход у потребителя может существовать и при отсутствии начального запаса товаров (за счет участия в прибыли производственного сектора). Последнее условие выполняется, если хотя бы одно производственное предприятие рентабельно и все потребители участвуют в прибыли производственного сектора (как минимум, не являются безработными). Это условие представляется не столь жестким и, следовательно, существование экономического равновесия - реальным. Однако здесь речь идет о моделях рынка, предполагающих выполнение не совсем реальных условий совершенной конкуренции.
Так как второе из условий не является жестким, то существование конкурентного равновесия, помимо условий У-1 - У-5, зависит от наличия положительного дохода у всех потребителей. Очевидно, что это условие слабее, чем У-6, так как положительный доход у потребителя может существовать и при отсутствии начального запаса товаров (за счет участия в прибыли производственного сектора). Последнее условие выполняется, если хотя бы одно производственное предприятие рентабельно и все потребители участвуют в прибыли производственного сектора (как минимум, не являются безработными). Это условие представляется не столь жестким и, следовательно, существование экономического равновесия - реальным. Однако здесь речь идет о моделях рынка, предполагающих выполнение не совсем реальных условий совершенной конкуренции.
Дата добавления: 2015-11-28; просмотров: 1296;
