Предельный анализ и эластичность в теории производства

Суть предельного анализа в экономической теории была рассмотрена при изучении теории потребления. Там же были приведены общие определения связанных с ним понятий средних и предельных величин, их относительных и процентных изменений, эластичности и предельной нормы замещения. Рассмотрим применение этих понятий в сфере производства. Многие методологические аспекты предельного анализа в производстве схожи с теми положениями для теории потребления.

Рассмотрим сначала понятие эластичности производства. Свойство однородности производственной функции оценивает технологию производства в различных точках пространства затрат. А именно, производственная функция в одних точках этого пространства может характеризоваться постоянным доходом от расширения масштаба производства, а в других - его увеличением или, наоборот, уменьшением. Локальным показателем измерения дохода от расширения масштаба производства и служит эластичность производства, которую будем обозначать символом 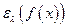(эластичность f по 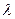в точке 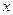). Формально (см. (2.3.2)) имеем:

.

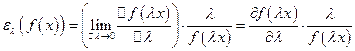Однако это соотношение не отражает изменение масштаба производства в точке 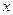. Поэтому вычислительная формула эластичности производства записывается в виде:

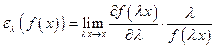
или

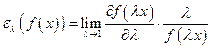. (3.3.1)

В случае постоянства дохода при расширении масштаба производства (т.е. для линейно-однородной производственной функции) эластичность производства равна единице. Действительно,

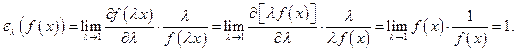
Пример 3.1. Вычислить эластичность производства, описываемого

a) функцией Кобба-Дугласа (3.2.4);

б) линейной функцией (3.2.9).

Для функции Кобба-Дугласа имеем:

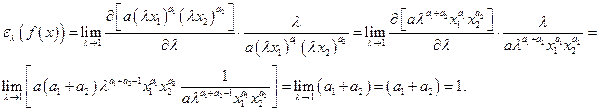
Для линейной производственной функции имеем:

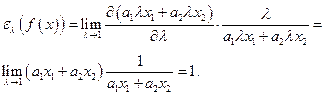
Можно показать, что в случае возрастания (убывания) дохода при изменении масштаба производства его эластичность больше (меньше) единицы.

Очевидно, предпочтение отдается производству с большей эластичностью, так как увеличивать затраты имеет смысл, если только это приводит к увеличению выпуска. Объективность оценки эластичности производства зависит от того, насколько адекватно производственная функция, как модель, отражает взаимосвязь затрат с выпуском. Можно говорить, что каждая производственная функция по-своему оценивает эластичность производства.

Для практического анализа производства также представляет интерес эластичность выпуска по видам ресурсов как величина, характеризующая процент прироста продукции при увеличении затрат на :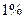

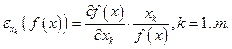(3.3.2)

Теорема 3.1. Эластичность производства, описываемого дифференцируемой линейноq однородной функцией, в любой точке пространства затрат равна сумме эластичностей выпуска по всем видам затрат.

Доказательство. Дифференцируя по 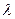обе части равенства 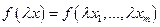по правилу дифференцирования сложной функции, находим:

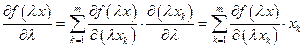
Пользуясь этим равенством, перепишем выражение (3.3.1) в виде

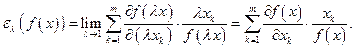
Здесь использовался факт линейной однородности производственной функции 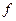. Следовательно, (см. (3.3.2))

,

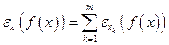а это и требовалось доказать.

Пример 3.2. Проверить утверждение теоремы 4.1 для производственных функций примера 4.1. Для функции Кобба-Дугласа имеем:

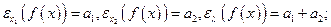
(см. пример 3.1); для линейной функции имеем:

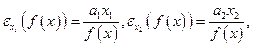
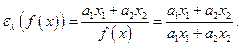
(см. пример 3.1).

На практике по разным причинам часто возникает необходимость замены одних ресурсов другими. Например, при расширении производства фирма должна решить: либо полностью автоматизировать производство за счет дорогостоящего оборудования и сократить количество рабочих мест (сократить фонд заработной платы), либо использовать предназначенные для этого средства для частичной модернизации технологии и увеличения фонда заработной платы. Что выгодно для фирмы? Для получения ответа на этот вопрос вводят понятия предельной нормы замещения одних ресурсов другими и эластичности замещения одних ресурсов другими.

Возможности замещения характеризуют производственную функцию с точки зрения различных комбинаций затрат, порождающих одинаковые уровни выпуска. Предположим, что двухфакторное производство описывается производственной функцией 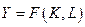, где Y - выпуск, K - капитал (основные фонды), L - трудовые ресурсы. Предположим, часть рабочих 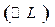уволилась. На какую величину 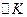следует увеличить основные фонды, чтобы выпуск остался на прежнем уровне, т.е. чтобы имело место равенство 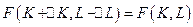? Используя равенства (2.3.5)-(2.3.10), получаем, что количество основных фондов необходимо увеличить на величину

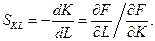
Число 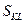называется предельной нормой замещения трудовых ресурсов основными фондами. Можно показать, что 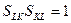. Например, для функции Кобба-Дугласа (3.2.4):

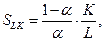
т.е. предельная норма замещения прямо пропорциональна фондовооруженности - чем больше фондовооруженность, тем выше уровень компенсации одной единицы трудовых ресурсов основными фондами.

В общем случае, т.е. для производственной функции 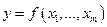, формула для вычисления предельной нормы замещения 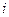-го ресурса k-м ресурсом имеет вид:

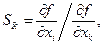
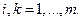
Из формул (3.3.2) и (3.3.3) вытекает взаимосвязь между эластичностью и предельной нормой замещения: для любых 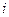и

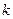
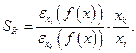
Отсюда, в частности, следует вывод о том, что для тех ресурсов, по которым выпуск неэластичен 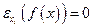, нет смысла говорить о предельной норме замещения ими других ресурсов. Дробь 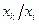, где 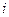- заменяемый, а 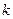- замещающий ресурсы, показывает, сколько единиц замещающего ресурса приходится на одну единицу заменяемого ресурса.

Таким образом, предельная норма замещения показывает величину ресурса одного вида, которой производитель готов пожертвовать ради одной единицы ресурса другого вида. Поставим обратный вопрос: как изменится величина 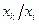при изменении предельной нормы замещения 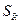на 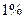? Согласно определения эластичности, это есть эластичность 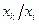по 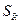. По формуле вычисления эластичности (2.3.2) находим:

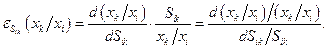(3.3.4)

Величина 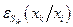называется эластичностью предельной нормы замещения (или просто эластичностью замещения). Обозначим 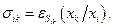С учетом известной формулы

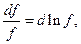
где 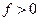, эластичность (3.3.4) можно представить в виде:

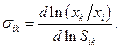(3.3.5)

Для практики особый интерес представляет случай постоянства эластичности замещения, т.е. независимость отношения 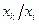от предельной нормы замещения .

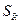Покажем, что таким свойством обладает производственная функция CES (для простоты рассмотрим случай двухфакторного производства (см. (3.2.5)). Для этого вычислим сначала предельную норму замещения для функции CES:

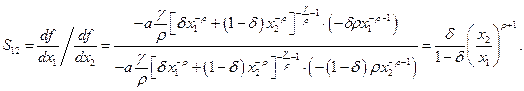
Подставляя это выражение в формулу (3.3.4), получим:

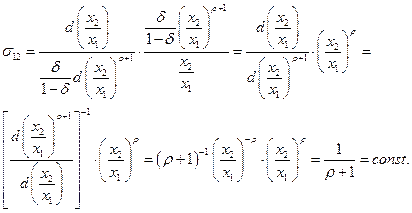
Аналогичным образом можно показать, что 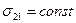и, более того, 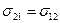. Поэтому эластичность замещения для функции CES можно обозначить как 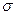. Очевидно,

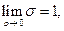
(3.3.6)

Нулевая эластичность означает отсутствие замещения. В общем случае, чем больше величина 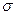, тем шире возможность замещения одних ресурсов другими. Стремление значения 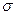к бесконечности означает, что каждый ресурс используется независимо от других. Представляет интерес вопрос: в каких ситуациях или при каких особых условиях производства такие случаи имеют место?

Заметим, что к классу производственных функций с постоянной эластичностью относится и функция Кобба-Дугласа. Для нее 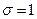. Поэтому с учетом (3.3.6) можно сказать, что при 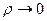производственная функция CES идентична с функцией Кобба-Дугласа. Можно доказать, что при 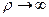функция CES идентична производственным функциям с фиксированными пропорциями (3.2.6) и Леонтьева (3.2.7) .