Основы классической механики

Механика – раздел физики, изучающий законы механического движения тел.

Тело – вещественный материальный объект.

Механическое движение – изменение положения тела или его частей в пространстве с течением времени.

Аристотель представлял такой вид движения как непосредственную перемену телом своего места относительно других тел, поскольку в его физике материальный мир был неразрывно связан с пространством, существовал вместе с ним. Время он считал мерой движения тела. Изменение в дальнейшем взглядов на природу движения привело к постепенному отделению пространства и времени от физических тел. Наконец, абсолютизация пространства и времени Ньютоном вообще вывела их за пределы возможного опыта.

Однако, этот подход позволил к концу XVIII века построить законченную систему механики, называемую теперь классической. Классичность заключается в том, что она:

1) описывает большинство механических явлений в макромире, используя небольшое число исходных определений и аксиом;

2) строго обоснована математически;

3) часто используется в более специфических разделах науки.

Опыт показывает, что классическая механика применима к описанию движения тел со скоростями υ << с ≈ 3·10⁸ м/с. Ее основные разделы:

1) статика изучает условия равновесия тел;

2) кинематика – движение тел без учета его причин;

3) динамика – влияние взаимодействия тел на их движение.

Основные понятия механики:

1) Механическая система – мысленно выделенная совокупность тел, существенных в данной задаче.

2) Материальная точка – тело, формой и размерами которого можно пренебречь в рамках данной задачи. Тело может быть представлено в виде системы материальных точек.

3) Абсолютно твердое тело – тело, расстояние между любыми двумя точками которого не меняется в условиях данной задачи.

4) Относительность движения заключается в том, что изменение положения тела в пространстве может быть установлено только по отношению к каким-то другим телам.

5) Тело отсчета (ТО) – абсолютно твердое тело, относительно которого рассматривается движение в данной задаче.

6) Система отсчета (СО) = {ТО + СК + часы}. Начало системы координат (СК) совмещают с какой-нибудь точкой ТО. Часы измеряют промежутки времени.

Декартова СК:

1. ; ;

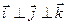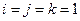2. ; ; .

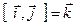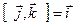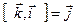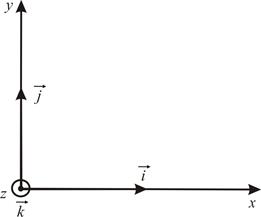
Рисунок 5

Положение материальной точки М описывается радиусом-вектором точки 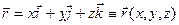, 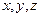– ее проекции на оси координат.

Если задать начальный момент времени t₀ = 0, то движение точки М опишется вектор-функцией 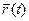или тремя скалярными функциями x(t), y(t), z(t).

Линейные характеристики движения материальной точки:

1) траектория – линия движения материальной точки (геометрическая кривая),

2) путь (S) – расстояние, пройденное вдоль нее за промежуток времени ,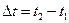

3) перемещение ,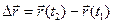

4) скорость ,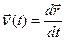

5) ускорение .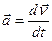

Любое движение твердого тела можно свести к двум основным видам – поступательному и вращательному вокруг неподвижной оси.

Поступательное движение – такое, при котором прямая, соединяющая любые две точки тела, остается параллельной своему первоначальному положению. Тогда все точки движутся одинаково, и движение всего тела можно описать движением одной точки.

Вращение вокруг неподвижной оси – такое движение, при котором существует прямая, жестко связанная с телом, все точки которой остаются неподвижными в данной СО. Траектории остальных точек – окружности с центрами на этой прямой. В этом случае удобны угловые характеристики движения, которые одинаковы для всех точек тела.

Угловые характеристики движения материальной точки:

1) угол поворота (угловой путь) 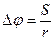, измеряемый в радианах [рад], где r – радиус траектории точки,

2) угловое перемещение 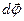, модуль которого представляет собой угол поворота за малый промежуток времени dt,

3) угловая скорость ,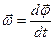

4) угловое ускорение .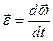

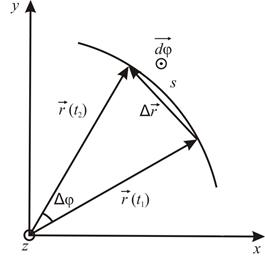
Рисунок 6

Связь между угловыми и линейными характеристиками:

, , .

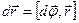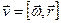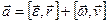Динамика использует понятие силы 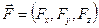, измеряемой в ньютонах (H), как меры воздействия одного тела на другое. Это воздействие является причиной движения.

Принцип суперпозиции сил – результирующий эффект воздействия на тело нескольких тел равен сумме эффектов воздействий каждого из этих тел в отдельности. Величина 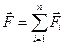называется равнодействующей силой и характеризует эквивалентное воздействие на тело n тел.

Законы Ньютона обобщают опытные факты механики.

1-й закон Ньютона. Существуют системы отсчета, относительно которых материальная точка сохраняет состояние покоя или равномерного прямолинейного движения при отсутствии силового воздействия на нее, т.е. если 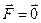, то .

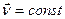Такое движение называется движением по инерции или инерциальным движением, и поэтому системы отсчета, в которых выполняется 1-й закон Ньютона, называются инерциальными (ИСО).

2-й закон Ньютона. 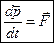, где 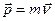– импульс материальной точки, m – ее масса, т.е. если 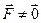, то 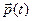и, следовательно, движение уже не будет инерциальным.

3-й закон Ньютона. При взаимодействии двух материальных точек возникают силы 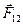и 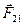, приложенные к обеим точкам, причем .

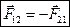В неинерциальных системах отсчета законы Ньютона не имеют ясного физического смысла и их можно использовать лишь формально, вводя в уравнения фиктивные силы инерции .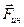

Обобщение этих законов на движение твердого тела дает уравнение динамики поступательного движения: 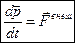, где , ;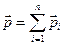

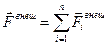и вращательного движения: 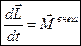, где , , , .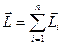

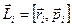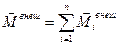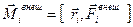Здесь 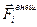и 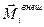– соответственно сила и момент силы, действующие на i – элемент тела со стороны внешних тел; 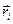– радиус-вектор этого элемента; 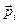– его импульс; 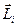– момент импульса.

Тело мысленно представляется в виде системы n элементов (материальных точек).