Направление возможного изменения частоты вращения двигателя (зона регулирования).

При номинальных условиях работы (напряжении и частоте питающей сети) двигатель имеет естественную механическую характеристику.При регулировании частоты вращения соответствующие им характеристики будут отличаться от естественной.Эти характеристики носят название искусственных (регулировочных) характеристик.С помощью одних методов регулирования удается получить искусственные характеристики, располагающиеся только ниже естественной.Другие методы обеспечивают регулирование частоты вращения выше и ниже естественной характеристики.Экономичность регулирования определяется по дополнительным капитальным затратам, необходимым при создании регулировочных устройств, а также по потерям электроэнергии при регулировании.

Следует отметить, что в ряде случаев, например для механизмов, работающих сравнительно малое время на искусственных характеристиках, потери электроэнергии даже при неэкономичных способах регулирования будут невелики (работа на низких доводочных скоростях лифтов, кранов и др.).При этом более рационально применение простых и дешевых способов регулирования частоты вращения двигателей, даже и неэкономичных с точки зрения потребления энергии.

Допустимая нагрузка двигателя при работе его на регулировочных характеристиках ограничивается величинами токов в статорной и роторных цепях.Эта нагрузка определяется допустимым нагревом двигателя и во многом определяется механическими характеристиками производственных механизмов, моментом сопротивления на валу, моментом инерции двигателя и механизма и т. д.

Регулирование частоты вращения асинхронных двигателей может производиться способом воздействия на него со стороны статора или со стороны ротора.Все три способа нашли широкое применение на практике.Рассмотрим эти способы подробнее.

Регулирование частоты вращения изменением частоты питающей сети является наиболее экономичным способом регулирования и позволяет получить хорошие механические характеристики электропривода.При изменении частоты питающей сети обеспечивается изменение частоты вращения магнитного поля асинхронного двигателя. Источник питания двигателя должен осуществлять преобразование напряжения стандартной частоты сети 50 Гц в напряжение с требуемой частотой. Одновременно с изменением частоты должна регулироваться по определенному закону и величина подводимого к двигателю напряжения, чтобы обеспечить высокую жесткость механической характеристики и требуемую перегрузочную способность двигателя. При регулировании частоты вращения асинхронных двигателей изменением частоты питающей сети можно обеспечить различные режимы работы: с постоянным вращающим моментом; с постоянной мощностью на валу; с моментом, пропорциональным квадрату частоты.

Зависимости между регулируемыми напряжением и частотой с учетом влияния активного сопротивления статора, изменения жесткости механических характеристик, насыщения стали, ухудшения теплоотдачи на низких частотах вращения ротора двигателя имеют довольно сложный характер.В качестве источника питания могут применяться электромашинные вращающиеся преобразователи, использующие электрические машины, или статические преобразователи частоты на полупроводниковых приборах, которые серийно выпускает промышленность.Положительным свойством частотного регулирования является возможность плавного регулирования в широком диапазоне в обе стороны от естественной характеристики (в том числе возможно вращение двигателя с частотой, большей номинальной).При регулировании обеспечивается жесткость характеристик и высокая перегрузочная способность.Однако в ряде случаев в приводах металлообрабатывающих станков, электрошпинделей, мощных воздуходувок и других механизмов частотное регулирование является наиболее приемлемым.

Регулирование частоты вращения изменением числа полюсов в обмотке статора обеспечивается благодаря изменению частоты вращения магнитного поля статора.При неизменной частоте питающей сети частота вращения магнитного поля и определяемая ею частота вращения ротора изменяются обратно пропорционально числу полюсов. Так как число полюсов, фиксированное ступенями, может быть равно 2, 4, 6, 8, 10 и т. д., что при частоте питающей сети, равной 50 Гц, соответствует синхронной частоте вращения 3000, 1500, 1000, 750, 600 об/мин и т. д., то указанным способом может быть обеспечено только ступенчатое регулирование.

Кроме двухскоростных асинхронных двигателей нашли применение трехскоростные и четырехскоростные двигатели.В трехскоростных двигателях размещаются одна переключаемая и одна непереключаемая обмотка, а в четырехскоростных — две переключаемые обмотки, позволяющие получить четыре синхронные частоты вращения, например 3000/1500/1000/500 об/мин.Двигатели с переключением числа пар полюсов, как правило, имеют короткозамкнутый ротор с обмоткой типа беличьей клетки.Такой ротор обеспечивает возможность работы без дополнительных пересоединений в его цепи.В случае фазного ротора в многоскоростных двигателях потребовалось бы производить переключения одновременно на статоре и роторе, что усложнило бы конструкцию ротора и эксплуатацию таких машин.К положительным показателям многоскоростных асинхронных двигателей следует отнести экономичность и относительно большой диапазон регулирования частоты вращения ротора.Недостатком данного способа регулирования является указанная выше невозможность плавного изменения частоты вращения.

Как отмечалось, в рамках единой общепромышленной серии асинхронных двигателей 4А выпускается модификация многоскоростных двигателей, предназначенных для работы на двух, трех или четырех скоростях.Регулирование частоты вращения изменением скольжения является одним из простых способов регулирования.В то же время при изменении (увеличении) скольжения изменяются (увеличиваются) потери в обмотке ротора, что приводит к уменьшению КПД при регулировании.

Регулирование скольжения можно осуществлять как со стороны статора, так и со стороны ротора.Естественно, что во втором случае ротор должен быть фазным и иметь выведенную на контактные кольца обмотку.При регулировании со стороны статора изменяют приложенное к его обмотке напряжение.Увеличение напряжения сверх номинального приводит к насыщению магнитной цепи двигателя и потому не применяется.

Для регулирования частоты вращения уменьшают напряжение питания.При этом развиваемый двигателем момент изменяется пропорционально квадрату напряжения и соответственно изменяются механические характеристики двигателя, в результате чего изменяются и значения рабочих скольжений.При регулировании со стороны ротора в основном применяется реостатное регулирование частоты вращения путем введения в цепь обмотки ротора добавочных активных сопротивлений (резисторов).При этом важно заметить, что изменение в широких пределах частоты вращения двигателя при данном способе регулирования не повлечет за собой изменения максимального (критического) момента.Таким образом, перегрузочная способность двигателя при регулировании не снижается.

40. Синхронные двигатели.
Конструкция, принцип действия

В отличие от асинхронного двигателя частота вращения синхронного двигателя
постоянная при различных нагрузках. Синхронные двигатели находят применение для привода машин постоянной скорости (насосы, компресоры, вентиляторы).
В статоре синхронного электродвигателя размещается обмотка, подключаемая к сети трехфазного тока и образующая вращающееся магнитное поле. Ротор двигателя состоит из сердечника с обмоткой возбуждения. Обмотка возбуждения через контактные кольца подключается к источнику постоянного тока. Ток обмотки возбуждения создает магнитное поле, намагничивающее ротор.
Роторы синхронных машин могут быть явнополюсными (с явновыраженными полюсами) и неявнополюсными (с неявновыраженными полюсами). На рис. 12.10а изображен сердечник 1 явнополюсного ротора с выступающими полюсами. На полюсах размещены катушки возбуждения 2. На рисунке 12.10б изображен неявнополюсной ротор, представляющий собой ферромагнитный цилиндр 1. На поверхности ротора в осевом направлении фрезеруют пазы, в которые укладывают обмотку возбуждения 2.

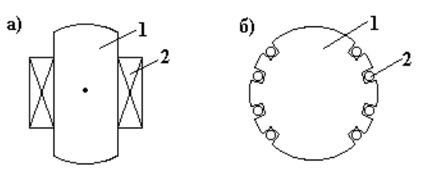
Рис. 12.10

Рассмотрим принцип работы синхронного двигателя на модели (рис. 12.11).

Вращающееся магнитное поле статора представим в виде магнита 1. Намагниченный ротор изобразим в виде магнита 2. Повернем магнит 1 на угол α. Северный магнитный полюс магнита 1 притянет южный полюс магнита 2, а южный полюс магнита 1 - северный полюс магнита 2. Магнит 2 повернется на такой же угол α. Будем вращать магнит 1. Магнит 2 будет вращаться вместе с магнитом 1, причем частоты вращения обоих магнитов будут одинаковыми, синхронными,
n₂ = n₁.

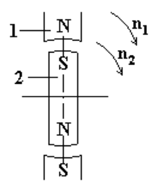
Рис. 12.11

Синхронный двигатель, на роторе которого отсутствует обмотка возбуждения, называется синхронным реактивным двигателем.
Ротор синхронного реактивного двигателя изготавливается из ферромагнитного материала и должен иметь явновыраженные полюсы. Вращающееся магнитное поле статора намагничивает ротор. Явнополюсный ротор имеет неодинаковые магнитные сопротивления по продольной и поперечной осям полюса. Силовые линии магнитного поля статора изгибаются, стремясь пройти по пути с меньшим магнитным сопротивлением. Деформация магнитного поля вызовет, вследствие упругих свойств силовых линий, реактивный момент, вращающий ротор синхронно с полем статора.
Если к вращающемуся ротору приложить тормозной момент, ось магнитного поля ротора повернется на угол θ относительно оси магнитного поля статора.
С увеличением нагрузки этот угол возрастает. Если нагрузка превысит некоторое допустимое значение, двигатель остановится, выпадет из синхронизма.
У синхронных двигателей отсутствует пусковой момент. Это объясняется тем, что электромагнитный вращающий момент, воздействующий на неподвижный ротор, меняет свое направление два раза за период Т переменного тока. Из-за своей инерционности, ротор не успевает тронуться с места и развить необходимое число оборотов.
В настоящее время применяется асинхронный пуск синхронного двигателя. В пазах полюсов ротора укладывается дополнительная короткозамкнутая обмотка.
Вращающее магнитное поле статора индуктирует в короткозамкнутой пусковой обмотке вихревые токи. При взаимодействии этих токов с магнитным полем статора образуется асинхронный электромагнитный момент, приводящий ротор во вращение. Когда частота вращения ротора приближается к частоте вращения статорного поля, двигатель втягивается в синхронизм и вращается с синхронной скоростью. Короткозамкнутая обмотка не перемещается относительно поля, вихревые токи в ней не индуктируются, асинхронный пусковой момент становится равным нулю.

41. Описать метод непосредственного применения законов Кирхгофа при анализе сложных электрических цепей с несколькими источниками энергии на следующем примере:

На рис. изображена схема разветвленной электрической цепи. Известны величины сопротивлений и 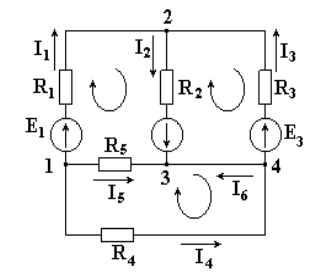ЭДС, необходимо определить токи.Укажем произвольно направления токов. Если в схеме имеется n узлов, количество независимых уравнений, которые можно составить по первому закону Кирхгофа, равно n - 1.

Для схемы на рис. 4.1 число независимых уравнений равно трем.

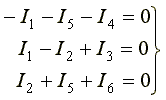(4.1)

Недостающее количество уравнений составляют по второму закону Кирхгофа. Уравнения по второму закону составляют для независимых контуров. Независимым является контур, в который входит хотя бы одна новая ветвь, не вошедшая в другие контуры.
Выберем три независимых контура и укажем направления обхода контуров. Запишем три уравнения по второму закону Кирхгофа.

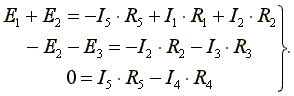(4.2)

Решив совместно системы уравнений (4.1) и (4.2), определим токи в схеме.
Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.

42. Описать метод контурных токов при анализе сложных электрических цепей с несколькими источниками энергии на следующем примере:

Метод применения законов Кирхгофа громоздок. Имеется возможность уменьшить количество уравнений системы. Число уравнений, составленных по методу контурных токов, равно количеству уравнений, составляемых по второму закону Кирхгофа.

Метод контурных токов заключается в том, что вместо токов в ветвях определяются, на основании второго закона Кирхгофа, так называемые контурные токи, замыкающиеся в контурах.
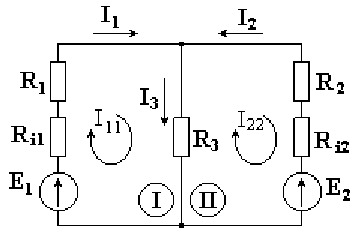
На рис. 4.2 в качестве примера изображена двухконтурная схема, в которой I₁₁ и I₂₂ - контурные токи.

Токи в сопротивлениях R₁ и R₂ равны соответствующим контурным токам. Ток в сопротивлении R₃, являющийся общим для обоих контуров, равен разности контурных токов I₁₁ и I₂₂, так как эти токи направлены в ветви с R₃ встречно.

Порядок расчета

Выбираются независимые контуры, и задаются произвольные направления контурных токов.
В нашем случае эти токи направлены по часовой стрелке. Направление обхода контура совпадает с направлением контурных токов. Уравнения для этих контуров имеют следующий вид:

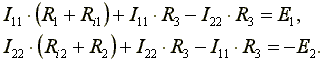
Перегруппируем слагаемые в уравнениях

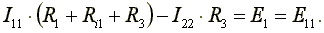(4.3)

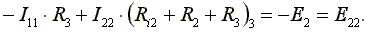(4.4)

Суммарное сопротивление данного контура называется собственным сопротивлением контура.
Собственные сопротивления контуров схемы

, .

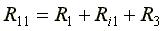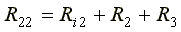Сопротивление R₃, принадлежащее одновременно двум контурам, называется общим сопротивлением этих контуров.

,

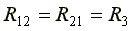где R₁₂ - общее сопротивление между первым и вторым контурами;
R₂₁ - общее сопротивление между вторым и первым контурами.
E₁₁ = E₁ и E₂₂ = E₂ - контурные ЭДС.
В общем виде уравнения (4.3) и (4.4) записываются следующим образом:

,

.

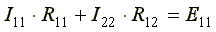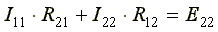Собственные сопротивления всегда имеют знак "плюс".
Общее сопротивление имеет знак "минус", если в данном сопротивлении контурные токи направлены встречно друг другу, и знак "плюс", если контурные токи в общем сопротивлении совпадают по направлению.
Решая уравнения (4.3) и (4.4) совместно, определим контурные токи I₁₁ и I₂₂, затем от контурных токов переходим к токам в ветвях.
Ветви схемы, по которым протекает один контурный ток, называются внешними, а ветви, по которым протекают несколько контурных токов, называются общими. Ток во внешней ветви совпадает по величине и по направлению c контурным. Ток в общей ветви равен алгебраической сумме контурных токов, протекающих в этой ветви.

43. Описать метод узловых потенциалов при анализе сложных электрических цепей с несколькими источниками энергии на следующем примере:

Метод узловых потенциалов позволяет составить систему уравнений, по которой можно определить потенциалы 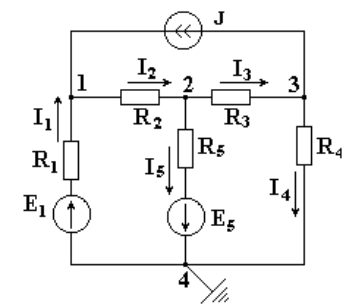всех узлов схемы. По известным разностям узловых потенциалов можно определить токи во всех ветвях. В схеме на рисунке 4.3 имеется четыре узла. Потенциал любой точки схемы можно принять равным нулю. Тогда у нас останутся неизвестными три потенциала. Узел, величину потенциала которого выбирают произвольно, называют базисным. Укажем произвольно направления токов. Примем для схемы φ₄ = 0.

Запишем уравнение по первому закону Кирхгофа для узла 1.

Рис. 4.3 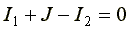(4.5)

В соответствии с законом Ома

,

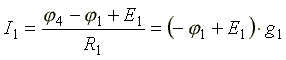где 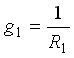- проводимость первой ветви.

,

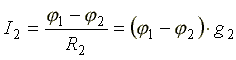где 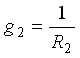- проводимость второй ветви.

Подставим выражения токов в уравнение (4.5).

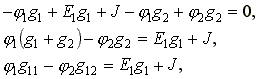(4.6)

где g₁₁ = g₁ + g₂ - собственная проводимость узла 1.

Собственной проводимостью узла называется сумма проводимостей ветвей, сходящихся в данном узле.
g₁₂ = g₂ - общая проводимость между узлами 1 и 2.
Общей проводимостью называют проводимость ветви, соединяющей узлы 1 и 2.
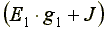- сумма токов источников, находящихся в ветвях, сходящихся в узле 1.
Если ток источника направлен к узлу, величина его записывается в правую часть уравнения со знаком "плюс", если от узла - со знаком "минус".
По аналогии запишем для узла 2:

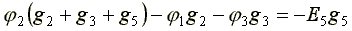(4.7)

для узла 3:

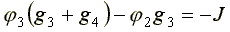(4.8)

Решив совместно уравнения (4.6), (4.7), (4.8), определим неизвестные потенциалы φ₁, φ₂, φ₃, а затем по закону Ома для активной или пассивной ветви найдем токи.
Если число узлов схемы - n, количество уравнений по методу узловых потенциалов - (n - 1).

Замечание. Если в какой-либо ветви содержится идеальный источник ЭДС, необходимо один из двух узлов, между которыми включена эта ветвь, выбрать в качестве базисного, тогда потенциал другого узла окажется известным и равным величине ЭДС. Количество составляемых узловых уравнений становится на одно меньше. .

44 Как рассчитываются последовательно соединенные реальная индуктивная катушка и конденсатор в цепи синусоидального тока?

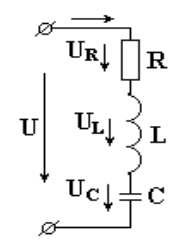
Катушка с активным сопротивлением R и индуктивностью L и конденсатор емкостью С включены последовательно (рис.6.8). В схеме протекает синусоидальный ток

.

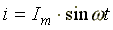Определим напряжение на входе схемы.
В соответствии со вторым законом Кирхгофа,

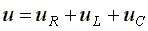
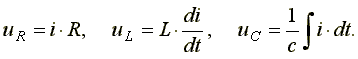(6.15)

Подставим эти формулы в уравнение (6.15). Получим:

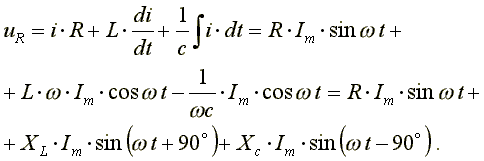(6.16)

Из выражения (6.16) видно: напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
Запишем уравнение (6.16) в комплексной форме:

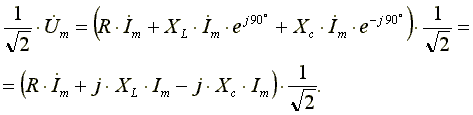(6.17)

Рис. 6.8

Поделим левую и правую части уравнения (6.17) на √2.
Получим уравнение для комплексов действующих значений токов и напряжений

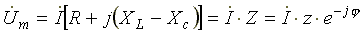, (6.18)

где 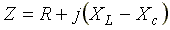- комплексное сопротивление цепи;
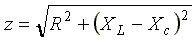- модуль комплексного сопротивления, или полное сопротивление цепи;
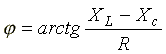- начальная фаза комплексного сопротивления.

При построении векторных диаграмм цепи рассмотрим три случая.

1. X_L > X_C, цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор напряжения на входе схемы опережает вектор тока (рис.6.9).

2. Индуктивное сопротивление меньше емкостного. Вектор напряжения на входе схемы отстает от вектора тока. Цепь носит емкостный характер(рис.6.10).

3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонансного напряжения (рис.6.11).

Ток в резонансном режиме достигает максимума, так как полное сопротивление (z) цепи имеет минимальное значение.

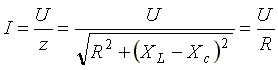
Условие возникновения резонанса: 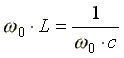, отсюда резонансная частота равна

.

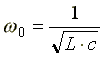Из формулы следует, что режима резонанса можно добиться следующими способами:

1. изменением частоты;

2. изменением индуктивности;

3. изменением емкости.

В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, во много раз превышающие напряжение на входе цепи. Это объясняется тем, что каждое напряжение равно произведению тока I₀(а он наибольший), на соответствующее индуктивное или емкостное сопротивление (а они могут быть большими).

.

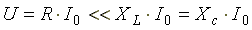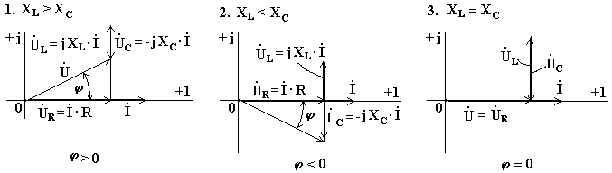
Рис. 6.9 Рис. 6.10 Рис. 6.11

45. Как рассчитываются параллельно соединенные индуктивность, емкость и активное сопротивление в цепи синусоидального тока?