Сложение взаимно перпендикулярных колебаний.

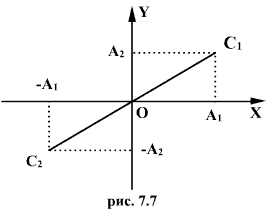
Пусть материальная точка одновременно участвует в двух гармонических колебаниях, совершающихся с одинаковыми периодами Т в двух взаимно перпендикулярных направлениях. С этими направлениями можно связать прямоугольную систему координат XOY, расположив начало координат в положении равновесия точки. Обозначим смещение точки С вдоль осей ОХ и OY, соответственно, через х и у. (рис 7.7)

Рассмотрим несколько частных случаев.

A. Начальные фазы колебаний одинаковы. Выберем момент начала отсчета времени таким образом, чтобы начальные фазы обоих колебаний были равны нулю. Тогда смещения вдоль осей ОХ и OY можно выразить уравнениями:

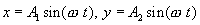
Поделив почленно эти равенства, получим уравнения траектории точки С:

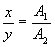или

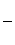
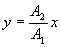
Следовательно, в результате сложения двух взаимно перпендикулярных колебаний точка С колеблется вдоль отрезка прямой, проходящей через начало координат (рис. 7.7).

Б. Начальная разность фаз равна π Уравнения колебания в этом случае имеют вид:

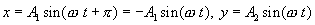
Уравнение траектории точки

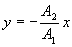
(7.15)

Следовательно, точка С колеблется вдоль отрезка 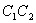прямой, проходящей через начало координат, но лежащие в других квадрантах, чем в первом случае. Амплитуда А результирующих колебаний в обоих рассмотренных случаях равна

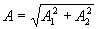
В. Начальная разность фаз равна .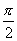

Уравнения колебаний имеют вид:

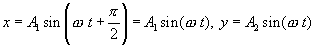
Разделим первое уравнение на 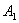, второе - на :

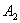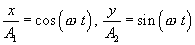
Возведем оба равенства в квадрат и сложим. Получим следующее уравнение траектории результирующего движения колеблющейся точки

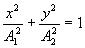
(7.16)

Колеблющаяся точка С движется по эллипсу с полуосям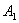и и 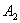. При равных амплитудах 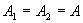траекторией суммарного движения будет окружность 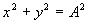В общем случае при 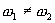, но кратным, т.е. 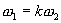, при сложении, взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу. Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.