Лекція 18 . Динамічні моделі маніпулятора. Структурні схеми моделей механічної частини маніпуляторів

Динамічні моделі дозволяють розв’язувати рівняння руху приводів окремих координат, тобто встановити, яким чином здійснюється рух окремих координат під дією моментів, що створюються приводом, який характер і ступінь взаємодії приводів різних координат один на одного при їх сумісній роботі.

При розв’язанні задачі вибору потужності привода динамічні моделі дозволяють за відомими часовими залежностями координат ланок маніпулятора знаходити часові залежності моментів приводів і будувати для них навантажувальні діаграми.

Побудова динамічних моделей вимагає попереднього запису рівняння Лагранжа ІІ роду для всіх узагальнених координат. Як показано вище, узагальнені сили знаходять за методом можливих переміщень. Знаходиться кінетична і потенційна енергія системи. Рівняння Лагранжа ІІ роду в явному вигляді універсальне, воно дозволяє отримати рівняння руху для всіх ланок маніпулятора.

Розглянемо процес складання рівнянь руху і побудови динамічних моделей на прикладі маніпуляторів, що працюють у полярній циліндричній системі координат. Для простоти зробимо припущення, що висувна частина руки невагома, а вся її маса зосереджена в центрі захвату.

Отже, для циліндричної системи координат знаходимо:

– узагальнені сили:

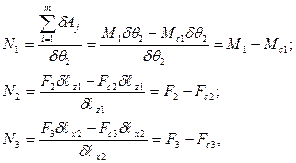
де M₁, F₂, F₃ – момент і сили, створювані приводами в ступенях рухомості; M_с1, F_с2, F_с3 – момент і сили опору в ступенях рухомості без урахування сили ваги;

– кінетична енергія системи:

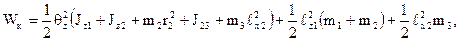
де враховано, що момент інерції відносно будь-якої осі 0ℓ, паралельній осі, котра проходить через центр мас і знаходиться на відстані r від неї, дорівнює J₁ = J + mr² (m – маса ланки, J – момент інерції ланки відносно осі, що проходить через центр мас); J_zi – момент інерції і–тої ланки відносно осі, що проходить через її центр мас і паралельно осі 0_iz_i;

– потенційна енергія

W_п =(m₂ + m₃)gℓ_х1.

Функція Лагранжа для цього маніпулятора буде

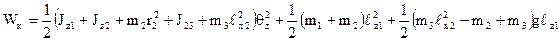
Виконаємо операції диференціювання, згідно з вимогами підстановки й отримаємо рівняння руху для трьох узагальнених координат маніпулятора:

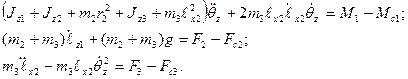
Ці рівняння дають повне уявлення про взаємовплив приводів один на один при їх сумісному русі. Вони показують, що момент двигуна повороту колони при заданому кутовому прискоренні змінюється при суміщенні двох координат θ_z i ℓ_х2 за рахунок появи сили Коріоліса і за рахунок зміни моменту інерції. В той же час при постійності лінійного прискорення ℓ_х2 змінюється сила, створювана приводом висування руки за рахунок появи відцентрової сили.

При висуванні руки (збільшенні моменту інерції) привід повороту руки повинен витратити більше енергії порівняно з незалежним рухом координат, а привід висування руки – менше енергії. Отже, привід повороту буде перевантажений, а привід висування недовантажений. При зменшенні ℓ_х2 (зменшення моменту інерції), навпаки, привід повороту буде недовантажений, а привід висування перевантажений.

Такий взаємовплив призводить до збільшення нерівномірності навантажувальної діаграми приводів, еквівалентного моменту двигунів і як наслідок завищення їх усталеної потужності.

Структурна схема динамічної моделі маніпулятора ПР, що працює у циліндричній системі координат, складена за вищевикладеними рівняннями, наведена на рисунку 18.1.

У цьому маніпуляторі взаємовпливу приводів повороту і висування руки немає, тобто привід підйому руки працює незалежно.

Рис. 18.1. Структурна схема моделі механічної частини ПР, що працює в циліндричній системі координат.

Динамічна модель для маніпулятора, що працює в сферичній системі координат

Рис. 18.2. Координатні осі ПР, що працює в сферичній системі координат.

Для такого маніпулятора (рис1 8.2) знаходимо:

– узагальнені сили

N₁ = M₁ – M_c1; (18.7)

N₂ = M₂ – M_c2; (18.8)

N₃ = F₃ – F_c3; (18.9)

– кінетичну енергію системи

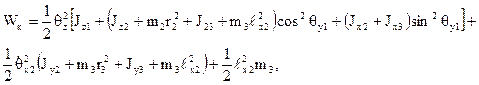
де враховано, що момент інерції відносно осі 0ℓ, яка проходить через центр мас у довільному напрямку, дорівнює:

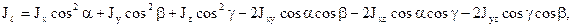
де 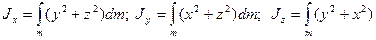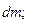- моменти інерції відносно осей, що проходять через центр мас ланки і паралельно осям системи 0_ix_iy_iz_i – що зв’язана з цією ланкою; 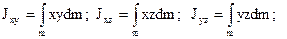– відцентрові моменти інерції відносно тих же осей (рівні нулю, якщо осі є головними осями інерції ланки); J_xi, J_yi, J_zi – моменти інерції і-тої ланки відносно тих же осей;

– потенційна енергія системи

W_п = (m₂r₂ + m₃ℓ_x2)×g×sinθ_y2.

Функція Лагранжа для цього маніпулятора має вигляд:

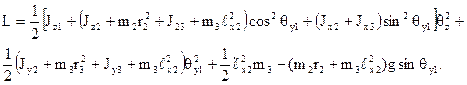(18.10)

Підставимо отриману функцію у рівняння Лагранжа ІІ роду в загальному вигляді, виконаємо диференціювання й отримаємо рівняння руху для всіх узагальнених координат маніпулятора:

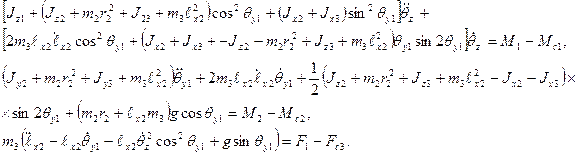
Отримані рівняння свідчать про значну взаємодію всіх трьох приводів при їх суміщеному русі. Так, момент привода повороту руки відносно осі 0z при постійному прискоренні 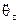буде вже залежати від двох коріолісових сил, що враховують взаємодію координат θ₂ і ℓ_х2, 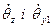. На привід висування руки будуть діяти відцентрові сили від швидкостей двох кутових координат, на приводи яких буде впливатиме зміна моментів інерції, зумовлена в свою чергу висуванням руки.