Лекция 14. Спонтанные и вынужденные переходы. Коэффициенты Эйнштейна.

Правила отбора

Возбужденный атом по истечении некоторого времени освобождается от излишка энергии с помощью испускания фотона. Это излучательные переходы. Существуют также безызлучательные переходы. Излучение отдельным возбужденным атомом происходит независимо от других атомов в разные моменты времени. Поэтому можно говорить о среднем времени жизниатома в возбужденном состоянии. Переходы возбужденных атомов с излучением происходят «сами собой». Это спонтанные, или самопроизвольные переходы. Излучение атомов при спонтанных переходах является некогерентным. Характерное время жизни атома в возбужденном состоянии 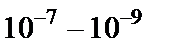с. В атомных масштабах это довольно большое время. Оно на много порядков больше периода колебаний излучения атома. Например, в оптическом диапазоне частота излучения 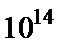Гц (период – 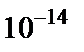с). Поэтому возбужденные состояния можно рассматривать как стационарные.

Существуют также вынужденные переходы, которые происходят под действием внешнего поля. В этом случае атомы поглощаютэнергию поля, переходя в возбужденное состояние, или вынужденно излучают, переходя в состояние с меньшей энергией. Если точно известно, что в начальный момент времени атом находится в некотором состоянии с энергией 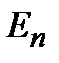, то вероятность этого события равна 1, т.е. величина 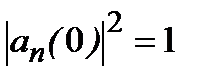. Под влиянием внешнего поля атом совершит переход в другое состояние с энергией 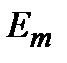. Вероятность того, что в момент времени t атом будет находиться в этом состоянии, определяется величиной 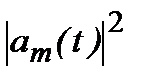, которая таким образом характеризует вероятность перехода из состояния n в состояние m. С такими вероятностями связаны коэффициенты Эйнштейна, играющие важную роль в теории излучения. Последовательное вычисление вероятностей перехода (и коэффициентов Эйнштейна) проводится с помощью решения уравнения Шредингера по теории возмущений. Ограничимся нестрогим подходом.

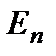Рассмотрим два состояния атома с энергиями и (при 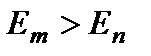) (рис.2.27). Вводится вероятность спонтанного перехода в единицу времени 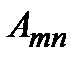из состояния 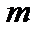в состояние 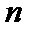. Величина 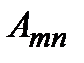имеет смысл среднего числа актов излучения в единицу времени, приходящихся на один атом. Допустим, что в момент времени в состоянии находится 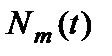атомов, образующих разреженный газ. За время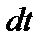

Рис.2.27 произойдет 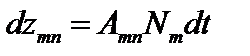переходов в состояние 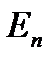. Величина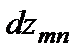

определяет уменьшение числа атомов, находившихся в момент времени в состоянии 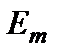: 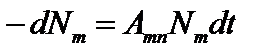. Решение этого уравнения:

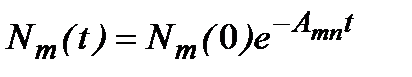. (2.76)

Величину 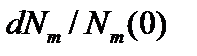есть мера вероятности спонтанного перехода атомов за время dt. Среднее время такого перехода (среднее время жизни атома в возбужденном состоянии m):

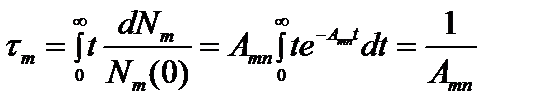.(2.77)

Таким образом, . Интенсивность излучения согласно (2.76) уменьшается со временем по закону:

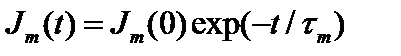. (2.77а)

Если атом, находящийся в состоянии 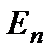, помещен во внешнее электромагнитное поле с частотой 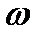, то он поглощает энергию поля при совпадении этой частоты с частотой 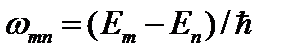и переходит в возбужденное состояние 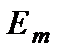. Пусть 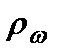– спектральная плотность энергии электромагнитного излучения. Вводят величину

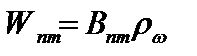. (2.78)

Это - вероятность поглощения излучения атомом в единицу времени.

Наряду с процессом поглощения, в результате которого происходит переход 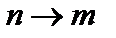, существует обратный процесс – вынужденное, стимулированное,или индуцированное испусканиепри переходе 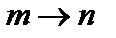под воздействием внешнего электромагнитного поля, частота которого равна частоте перехода. Такой процесс характеризуется величиной

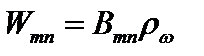. (2.78а)

Это - вероятность индуцированного излучения в единицу времени. 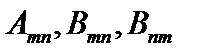- коэффициенты Эйнштейна. Коэффициенты Эйнштейна связаны соотношениями:

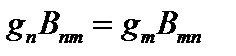, (2.79)

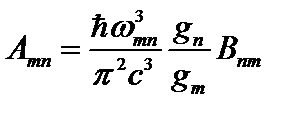. (2.79а)

Коэффициент (или 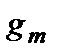) - статистический вес, или кратность вырождения -го (или -го) состояния.

Вычисление вероятностей перехода (коэффициентов Эйнштейна) проводится последовательно по правилам квантовой механики. Однако окончательные результаты можно получить с помощью простых полуклассических рассуждений. Электроны и положительное ядро представляют собой электрически нейтральную систему зарядов. Согласно классической электродинамике поле ограниченной электрически нейтральной системы движущихся зарядов можно представить в виде суммы полей мультиполей:– поле электрического диполя, поле электрического квадруполя и магнитного диполя и т.д. Разложение поля излучающей системы зарядов по мультиполям возможно, если линейный размер этой системы 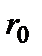мал по сравнению с длиной волны излучения :

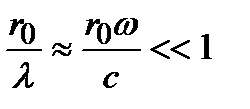. (2.80)

Поля электрического квадруполя и магнитного диполя в 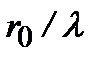раз меньше поля электрического диполя. В случае излучающего атома величина 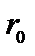определяется размерами атома: 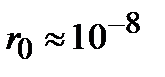см. В оптическом диапазоне длина волны 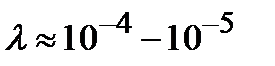см. Таким образом, для оптического диапазона 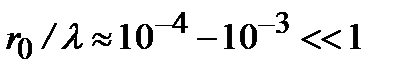. Основной тип излучения возбужденного атома - электрическое дипольное излучение. Мощность излучения электрического диполя (энергия, излучаемая диполем в единицу времени), колеблющегося с частотой 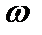, описывается формулой:

, (2.81)

где 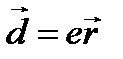– электрический дипольный момент. При спонтанном переходе за среднее время жизни атома высвечивается фотон с энергией 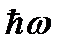. Следовательно, мощность излучения равна:

. (2.81а)

Из сравнения (2.81) и (2.81а):

. (2.82)

К такому же результату можно прийти с помощью строгого квантово–механического расчета. При этом под 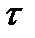надо понимать 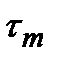, а под 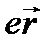– матричный элемент дипольного момента:

,

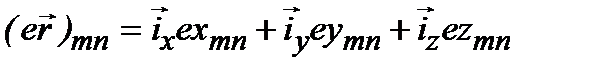где 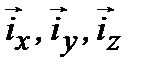– единичные векторы декартовой системы координат. Таким образом, вероятность спонтанного излучения в единицу времени:

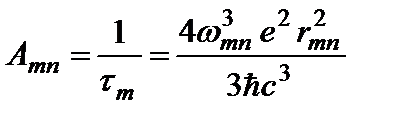. (2.83)

Здесь

. (2.83а)

Матричный элемент - среднее значение величины x при переходе из состояния 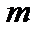в состояние :

, (2.84)

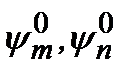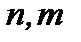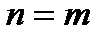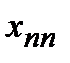где – собственные волновые функции атома в стационарных состояниях . Если , то - среднее значение величины 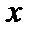(аналогично для переменных 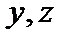) в собственном состоянии .

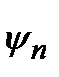Оценим среднюю величину дипольного момента в случае оптического излучения ( 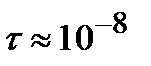с, частота 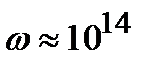Гц). Тогда 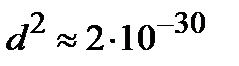СГС. Если такой же порядок (или меньше) дипольного момента сохраняется и в радиочастотном диапазоне ( 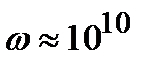Гц), то среднее время жизни атома оказывается очень большим: 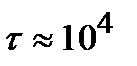с, а вероятность спонтанного перехода 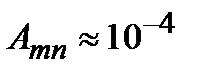c^-1. Это значит, что в радиочастотном диапазоне спонтанное излучение не имеет большого значения.

Согласно (2.83) вероятности излучательных переходов определяются значениями матричных элементов. Если эти элементы равны нулю, то равна нулю вероятность переходов - такие переходы не осуществляются. Они называются запрещенными.Матричные элементы отличны от нуля лишь при определенных ограничениях на изменение квантовых чисел при переходах из одного состояния в другое. Эти ограничения называют правилами отбора. Матричные элементы дипольных переходов вычисляются по формуле (2.84), если известны собственные волновые функции. Для линейного гармонического осциллятора собственные функции описываются формулой (2.44). Вычисления приводят к следующему результату: квантовое число , определяющее состояния осциллятора, при переходах может изменяться лишь на ±1:

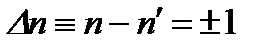. (2.85)

По формуле (2.43) частота перехода равна частоте классического осциллятора:

, (2.85а)

Для ротаторасобственные функции определяются формулой (2.57). Состояния квантового ротатора описываются квантовыми числами 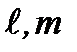. При переходах из состояния 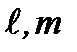в состояние 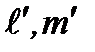правила отбора: для изменения орбитального квантового числа:

, (2.86)

для изменения магнитного квантового числа:

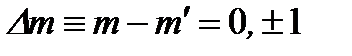. (2.87)

Эти правила определяют также поляризацию излучения.

Возможные изменения состояний ротатора связаны с законом сохранения четности. Инверсии 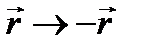в сферической системе координат ( 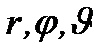) соответствует преобразование:

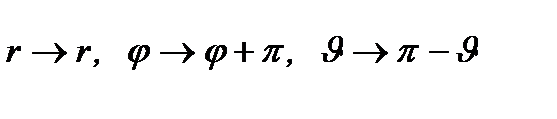. (2.89)

При таком преобразовании в волновых функциях состояний ротатора (2.57) происходят изменения: 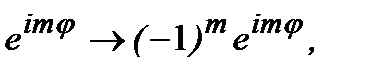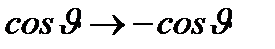. Согласно (2.56а): 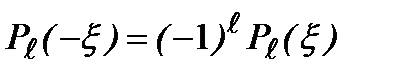, так что 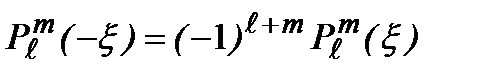. Таким образом, волновая функция при инверсии преобразуется по закону: .

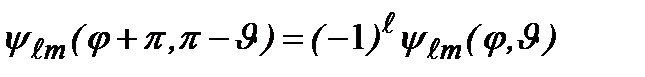Отсюда следует, что четность состояний ротатора определяется значением орбитального квантового числа 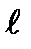. Если – четное число, то состояние четно. Если – нечетное число, то состояние – нечетно.

Матричные элементы определяются интегралами вида 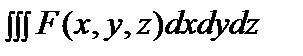в симметричных пределах от до 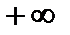. Интеграл отличен от нуля, если функция 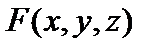– четная. Если она нечетная, то интеграл обращается в нуль. При дипольных переходах матричные элементы вычисляются по формуле (2.84). Подынтегральная функция 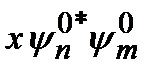должна быть четной. Величина x меняет свой знак при инверсии. Произведение также должно быть нечетной функцией. Таким образом, возможны переходы 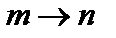лишь между состояниями с различной четностью.Это – правило Лапорта. Так как четность определяется значениями орбитального квантового числа, то отсюда следует правило (2.86). Дипольные переходы пр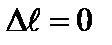и или являются запрещенными.

Вероятность квадрупольных переходов определяется матричными элементами:

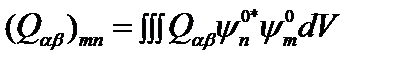, (2.90)

где 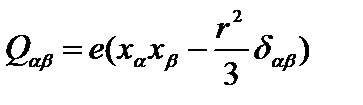– квадрупольный электрический момент - четная функция координат. В этом случае осуществляются переходы между состояниями с одинаковой четностью. Правило отбора при квадрупольных переходах: 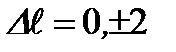. При этом переходы с 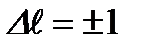запрещены.

Указанные правила отбора не всегда строго выполняются: наблюдаются спектральные линии, связанные с запрещенными переходами.