Лекция 12. Момент импульса. Квантовый ротатор.

В классической механике вектор момента импульса (момента количества движения) частицы относительно начала координат определяется формулой 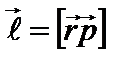. В квантовой механике в координатном представлении вектору импульса соответствует оператор импульса 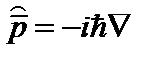. Поэтому можно ввести оператор момента импульса:

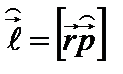. (2.46)

Декартовы компоненты этого оператора:

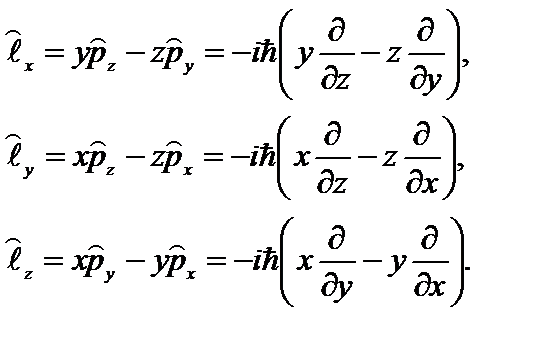(2.46a)

Более удобно рассматривать проекции оператора момента импульса не в декартовых, а в сферических координатах, которые связаны друг с другом соотношениями:

.

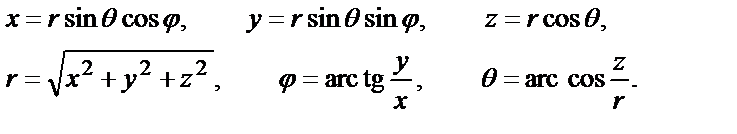В сферических координатах операторы:

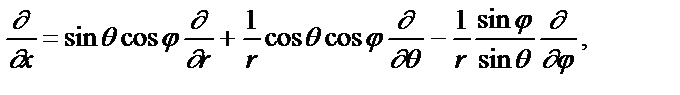
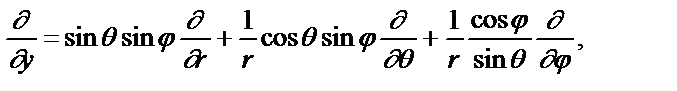
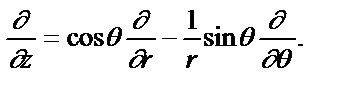
С помощью выписанных соотношений получаем выражения для проекций оператора момента импульса в сферических координатах:

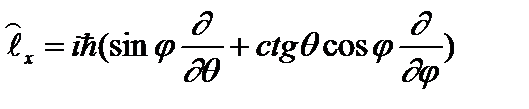, (2.47a)

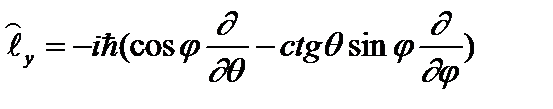, (2.47б)

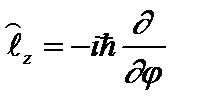. (2.47в)

Проекции оператора 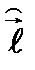определяются только угловыми переменными и не содержат зависимости от 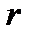. Рассмотрим оператор квадрата момента импульса:

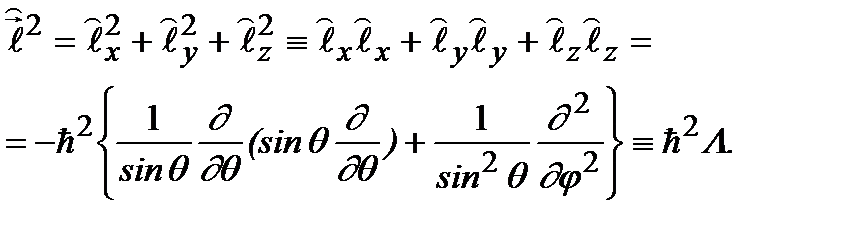(2.48)

Оператор 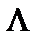оператор Лежандра.

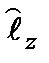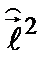Определим собственные функции и собственные значения операторов и . По общим правилам:

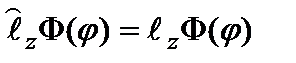. (2.49)

Собственные значения 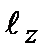определяют возможные проекции вектора момента импульса на ось 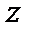. Они являются наблюдаемыми величинами. Учитывая выражение (2.47в), имеем уравнение:

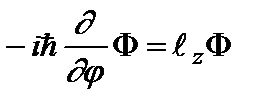. (2.49a)

Отсюда решение:

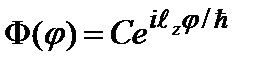, (2.49б)

где С – постоянная, определяемая условием нормировки. Функция 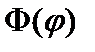является периодической с периодом 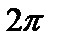и ограниченной. Условие однозначности волновой функции требует, чтобы ее значение через период повторилось: 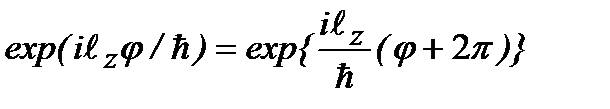. Отсюда следует: 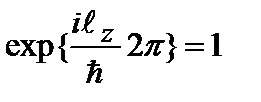. Это приводит к квантованным значениям проекции вектора момента импульса на ось :

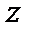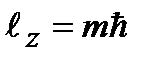. (2.50)

Целое число 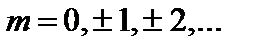магнитное квантовое число(Зоммерфельд, 1916).

Собственные функции оператора проекции момента импульса на ось 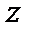согласно (2.49б),(2.50):

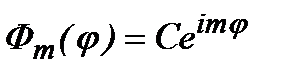. (2.51)

Эти функции образуют полную систему ортонормированных функций:

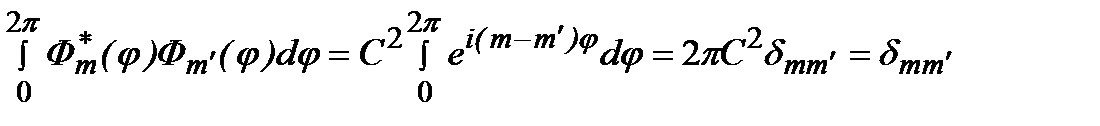, (2.51a)

где 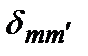– символ Кронекера. Таким образом, 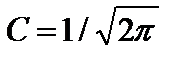. Аналогично формулируется задача на собственные значения оператора :

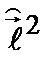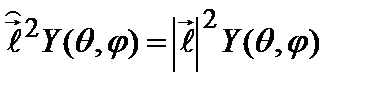, (2.52)

где 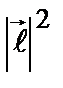– наблюдаемые значения квадрата модуля вектора момента импульса. Согласно (2.48) задача (2.52) совпадает с задачей на собственные значения оператора Лежандра:

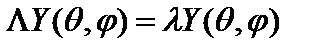, (2.53)

так что

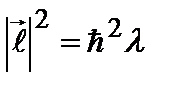. (2.53a)

Собственные значения оператора Лежандра можно найти с помощью следующего приема: рассмотрим уравнение Лапласа 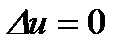для функции 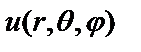в сферических координатах:

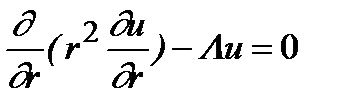, (2.54)

где 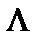– оператор Лежандра (2.48). Решение, не обращающееся в бесконечность при 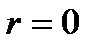, ищется в виде:

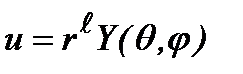, (2.54a)

где положительное целое число 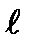= 0, 1, 2, …Тогда из (2.54):

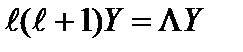. (2.54б)

Таким образом, 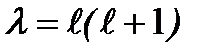. Следовательно,

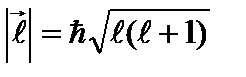, (2.55)

т.е. величина (длина) вектора момента импульса принимает дискретный набор значений в зависимости от значений числа 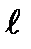. Это число - азимутальное, или орбитальное квантовое число.

Собственные функции оператора квадрата момента импульса - шаровые функции:

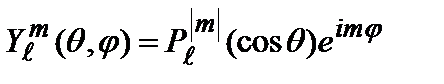, (2.56)

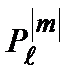– присоединенные полиномы Лежандра, определяемые формулой:

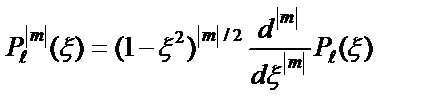, (2.56а)

где 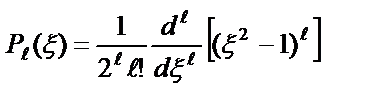– полиномы Лежандра.

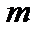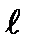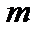В (2.56) число - магнитное квантовое число. При фиксированном значении квантового числа число принимает 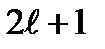значений:

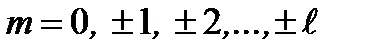. (2.56б)

В (2.56) множитель 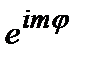- собственная функция (2.51) оператора 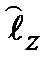. Это значит, что собственные функции оператора квадрата момента импульса являются одновременно собственными функциями оператора проекции момента импульса на ось z. Таким образом, модуль (длина) вектора момента импульса и его проекция на ось z являются одновременно измеряемыми величинами.

Ортонормированные волновые функции оператора квадрата момента импульса равны:

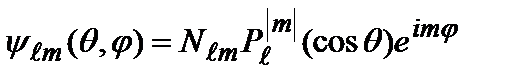, (2.57)

где постоянные нормировки .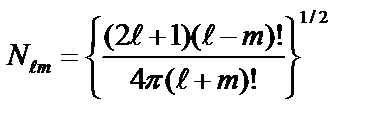

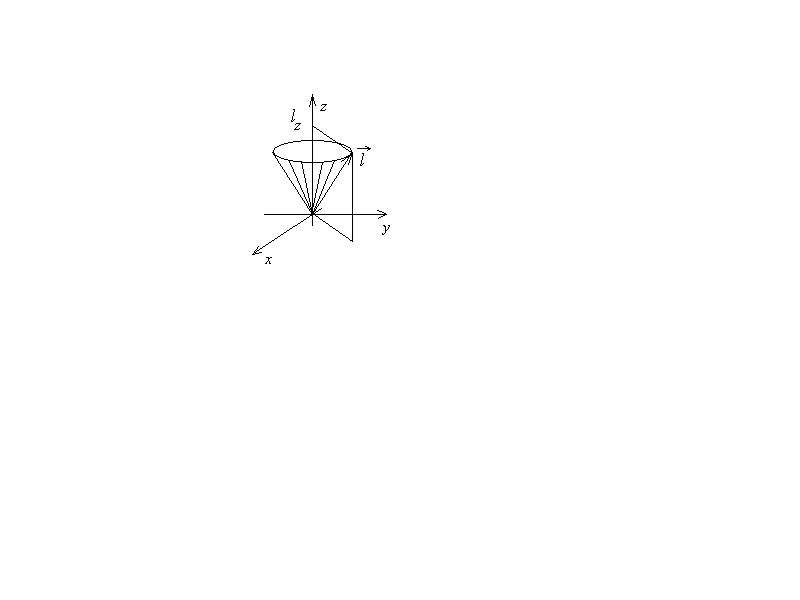Существуют ли все три проекции вектора момента импульса одновременно? Вспомним, что проекция вектора момента импульса на ось z и азимутальный угол 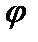являются парой канонически сопряженных переменных, для которых справедливо соотношение неопределенностей (1.75). Задание точного значения проекции 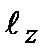означает, что угол 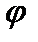при этом являетсянеопределенным. Так как модуль (длина) вектора момента импульса также задана точно, то вектор момента импульса оказывается расположенным на поверхности конуса (рис.2.16). Угол при вершине этого конуса определяется соотношением:

Рис.2.16 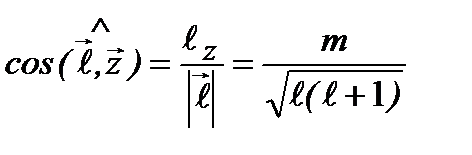. (2.58)

Так как азимутальный угол не имеет определенного значения, то проекции 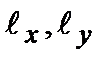являются неопределенными. Это значит, что операторы проекций вектора момента импульса не коммутируют друг с другом, но каждый из этих операторов коммутирует с оператором квадрата момента импульса. Действительно, можно убедиться, что

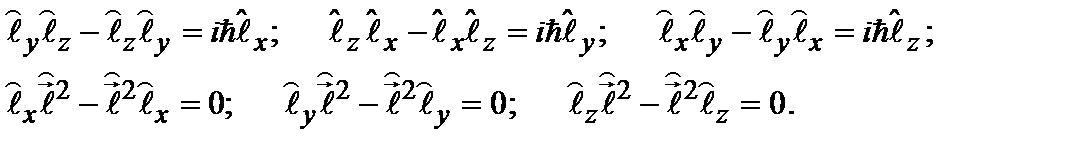(2.59)

Таким образом, можно говорить одновременно только о длине вектора момента импульса и одной из его проекций на некоторую выделенную ось. В качестве такой оси обычно выбирается ось z. Она может быть выделена, например, с помощью внешнего магнитного поля. Проекции вектора момента импульса на другие оси при этом остаются неопределенными.

Как видно из полученных соотношений, длина (модуль) вектора момента импульса 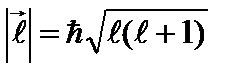всегда больше максимального значения проекции момента 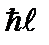. Если бы эти величины были равны друг другу, то две другие проекции в этом состоянии имели бы вполне определенное, нулевое значение. Но это невозможно. Вместе с тем, существует единственное состояние, в котором все три проекции вектора момента импульса имеют определенное значение. Это состояние с 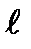=0, в котором все три проекции одновременно равны нулю. Волновая функция этого состояния 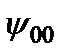, согласно (2.57), сводится к постоянной, так что она является собственной функцией всех трех операторов 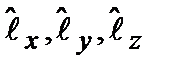, а углы 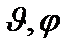при этом оказываются неопределенными.

В классической механике ротатор -это вращающаяся система жестко связанных друг с другом частиц. В квантовом случае такой образ лишен смысла, так как энергия при точном задании расстояния между частицами бесконечна. Само расстояние задается с определенной вероятностью. Однако окончательные результаты об энергии вращательного движения оказываются совпадающими с точным решением уравнения Шредингера в центрально–симметричном поле. Это связано с тем, что операторы проекций момента импульса и его квадрата не зависят от радиуса. С такой оговоркой рассмотрим кинетическую энергию ротатора 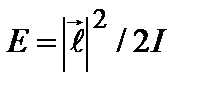, где 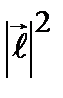– квадрат вектора момента импульса, 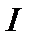– момент инерции. В квантовом случае величина 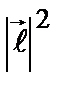квантуется согласно (2.55). Таким образом, приходим к формуле, определяющей энергетический спектр вращательного движения (ротатора):

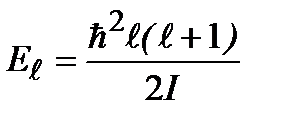. (2.60)

Состояния ротатора описываются с помощью волновых функций (2.57). Эти функции определяются как азимутальным, так и магнитным квантовыми числами. Так как при заданном значении орбитального квантового числа магнитное квантовое число принимает 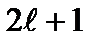различных значений, то столько же имеется различных волновых функций. Всем этим функциям отвечает одно и то же значение энергии (2.60). Состояния с некоторым значением энергии, которому соответствуют различные собственные функции, называются вырожденными состояниями.Число этих различных волновых функций называют кратностью вырождения состояний.Таким образом, каждое состояние ротатора является 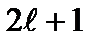– кратно вырожденным.

По историческим традициям, энергетические состояния, отвечающие фиксированному значению числа 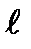, принято обозначать соответствующими буквами (таблица 2):

Таблица 2

Значения числа 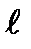0 1 2 3 4 5

Буквенное обозначение

состояния s p d f g h

Некоторые волновые функции состояний ротатора:

s–состояние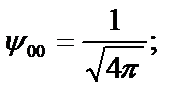

p–состояние 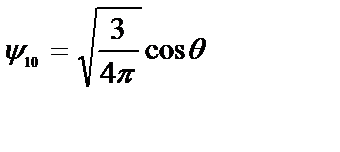, 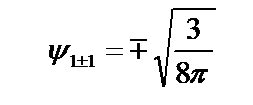sin ;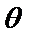

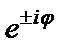d–состояние

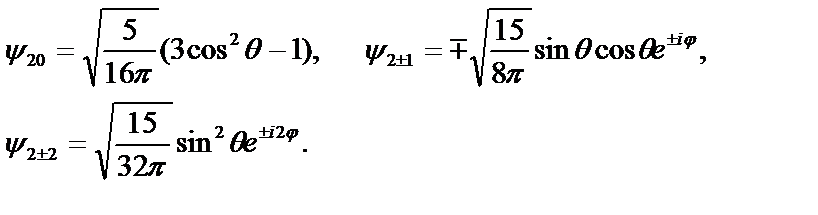(2.61)

Пространственную ориентацию квантового вектора момента импульса изображают графически (рис.2.17), при этом учитывается, что определенные значения имеют только 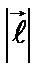и 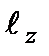, а проекции 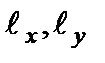являются принципиально неопределенными. Такие изображения называют пространственным квантованием.

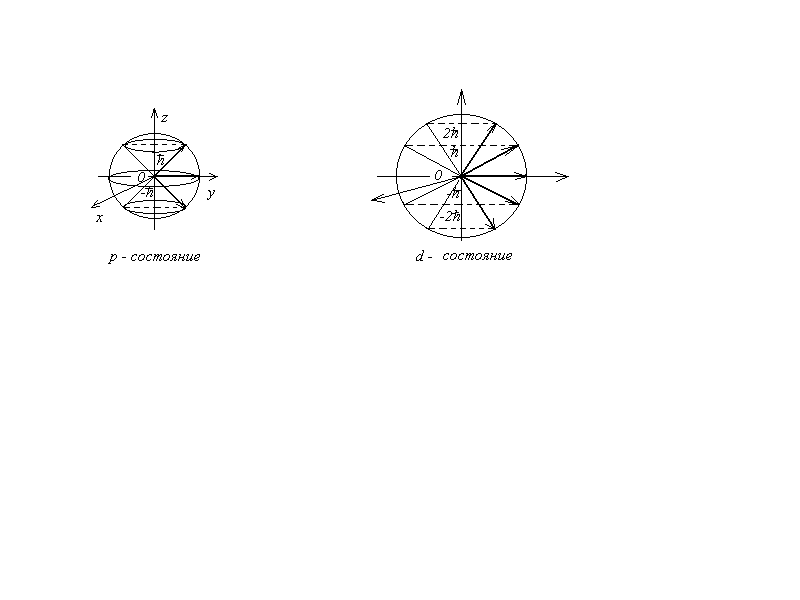
Рис.2.17

Поясним смысл пространственного квантования, которое связано с вырожденностью состояний, на примере р–состояния. Это состояние описывается тремя собственными функциями, которые выписаны выше. Волновая функция состояния представляет собой, в общем, линейную комбинацию трех волновых функций: 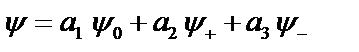. Поскольку пространство изотропно, то ни одно направление в нем не выделено. Если мы хотим найти проекцию момента импульса на какую-то ось, например, на ось z, то необходимо сначала выделить это направление. Это можно сделать, например, если включить магнитное поле в этом направлении, и затем измерить проекцию момента импульса на эту ось. В результате измерения величина проекции 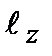будет одной из трех, например, 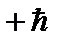. Тогда после измерения состояние описывается функцией 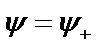. Это означает, что 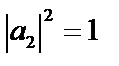, а . 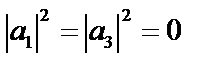Таким образом, проекция 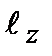имеет определенное значение, при этом о проекциях на другие оси ничего сказать нельзя. Если мы захотим определить проекцию момента импульса на другое направление, то его также необходимо выделить, при этом предшествующее состояние будет разрушено и возникнет новое состояние, в котором при измерении будет определена опять только одна проекция.

Плотность вероятностей различных состояний ротатора определяется с помощью волновых функций (2.57) по общим правилам:

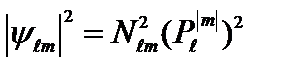. (2.62)

В отличие от классического ротатора, движение которого является плоским, движение квантового ротатора характеризуется углами 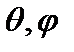и, условно говоря, происходит по поверхности сферы с фиксированным радиусом, который можно принять за единицу. Тогда формула (2.62) описывает плотность вероятностей состояний ротатора на поверхности сферы. Элемент этой поверхности:

.

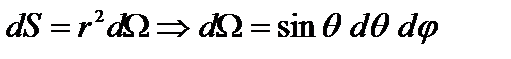Формула (2.62) показывает, что плотность вероятностей не зависит от азимутального угла 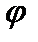. Это позволяет использовать диаграммы с учетом формул (2.61). На такой диаграмме (рис.2.18) отрезок от начала координат до некоторой точки на кривой определяет плотность вероятности найти частицу на поверхности единичной сферы в направлении угла 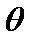при любом значении угла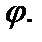

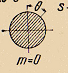
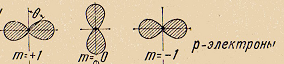
Рис.2.18

Для получения пространственной картины нужно «прокрутить» диаграмму вокруг оси z. Из приведенных диаграмм видно, что в s–состоянии имеется одинаковая вероятность найти частицу в любом месте на поверхности сферы. Это как раз – то состояние, в котором все три проекции момента импульса имеют определенное, нулевое значение. В остальных случаях вероятность зависит от магнитного квантового числа. Например, для p–состояния (р–электроны) при значении 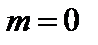вероятность максимальна в направлениях 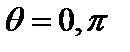, тогда как при 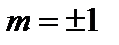максимум вероятности соответствует 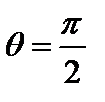, т.е. плоскости 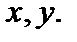Во всех случаях квантовая картина не имеет ничего общего с картиной классического ротатора, который вращается в плоскости 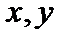вокруг оси z. Однако с возрастанием магнитного квантового числа плотность вероятностей для состояний с максимальным значением этого числа, характеризуется все меньшим отклонением от плоскости x, y. Действительно, как следует из формулы (2.58), при 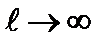угол между вектором 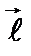и осью z стремитсяк нулю. В этом проявляется принцип соответствия.