Приложение. Выбор отношения давлений в ступенях многоступенчатого компрессора из условия минимума затрачиваемой на его сжатие работы

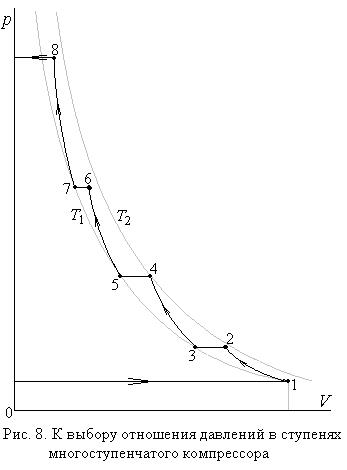Пусть сжатие газа в многоступенчатом компрессоре (m – число ступеней) происходит по политропе с одинаковым показателем n для каждой ступени, но с разными степенями повышения давления

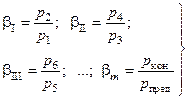
или в общем виде

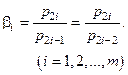
Предположим также, что в каждом из промежуточных охладителей газ охлаждается до его начальной температуры на всасе, т.е.

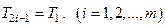
Произведение степеней повыше-ния давления во всех ступенях комп-рессора с учётом изобарности про-цессса охлаждения в промежуточных охладителях 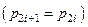оказыва-ется равным

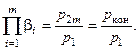
Прологарифмируем и затем вычислим полный дифференциал получившегося выражения с учётом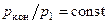

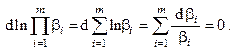
Вычислим затем первый дифференциал выражения для удельной работы компрессора (с учётом знака) в предположении неодинаковости степени повышения давления по ступеням

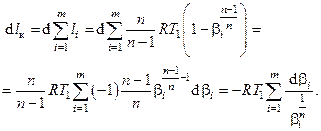
Метод неопределённых множителей Лагранжа предполагает тождественное равенство нулю суммы

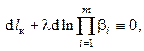
где λ – подлежащая определению постоянная, называемая множителем Лагранжа. С учётом и получаем

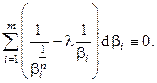
Для того, чтобы это равенство соблюдалось тождественно, необходимо и достаточно, чтобы коэффициенты при дифференциалах 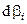были равными нулю, т.е.

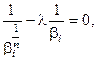
откуда следует

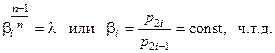
То, что найденный экстремум является минимумом, следует из того факта, что второй дифференциал выражения для работы многоступенчатого компрессора оказывается положительным. В самом деле

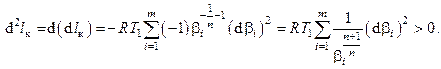
Из при условии следует, что при одинаковых во всех ступенях сжатия показателях политропы работа, затрачиваемая на сжатие в многоступенчатом компрессоре, будет минимальной, если степени повышения давления x_i в каждой ступени будут одинаковыми.