Из равенств и и при одинаковых показателях политроп сжатия n следует

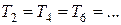
Найдём степени повышения давления в каждой из ступеней компрессора:

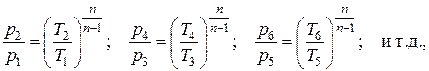
но имея в виду , и

т.е. при заданных условиях степень повышения давления x в каждой из m ступеней компрессора одинакова. Перемножив все m степеней повышения давлений с одинаковыми значениями, с учётом получим

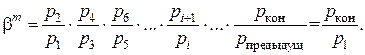
Это условие позволяет выбрать степень повышения давления в каждой ступени компрессора при заданном конечном давлении p_кон и при заданном числе ступеней m

Если же задана степень повышения давления x в каждой из ступеней компрессора, что определяется допустимым нагревом газа, то условие позволяет выбрать число ступеней компрессора согласно выражению

Очевидно, что рассчитанное по этой формуле значение m должно быть округлено до ближайшего целого числа с большей стороны.

Вычислим работу, затрачиваемую на сжатие газа в многоступенчатом компрессоре. Имеем для удельной работы

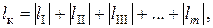
где суммирование ведётся по всем ступеням компрессора.

Имеем, следовательно,

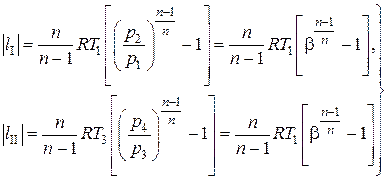
и т.д.

Отсюда видно, что при указанном выборе параметров компрессора затрачиваемая работа на сжатие во всех ступенях одинакова. Таким образом, удельная работа, затрачиваемая на сжатие газа в многоступенчатом компрессоре равна

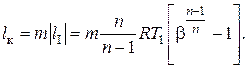
Теоретическая мощность, затрачиваемая на сжатие газа в многоступенчатом компрессоре при заданной производительности будет, очевидно, вычисляться по прежней формуле .

Рассчитаем теперь количество теплоты, которое необходимо отводить от газа в процессе его сжатия в ступенях компрессора и в промежуточных охладителях. Легко видеть, что при выбранных условиях равенства степеней повышения давления в каждой из ступеней все эти количества теплоты для отдельной ступени одинаковы. Итак, имеем для удельных величин:

а) в одной ступени сжатия

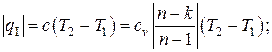
б) в одном промежуточном охладителе

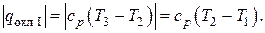
Тогда полное количество тепла (т.е. тепловая мощность), отводимого от сжимаемого газа в единицу времени, будет, очевидно,

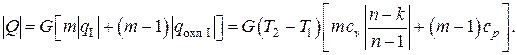
Здесь было учтено, что количество промежуточных охладителей на единицу меньше числа ступеней сжатия.