Массовый расход. Уравнение неразрывности
Весьма важной характеристикой течения газа (пара) является массовый расход G, т.е. масса вещества, протекающего через поверхность площадью f в единицу времени. При течении газа в каналах в одномерном приближении массовый расход определится следующим образом:
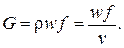 (7.9)
(7.9)
Здесь ρ=1/v – плотность газа (пара), кг/м3; v – удельный объём, м3/кг.
Определение массового расхода (7.9) может быть записано в дифференциальной форме. Для этого сначала вычислим логарифм расхода 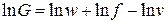 , а затем применим операцию взятия дифференциала от каждого слагаемого. В результате получим
, а затем применим операцию взятия дифференциала от каждого слагаемого. В результате получим
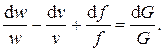 (7.10)
(7.10)
Если стенки канала непроницаемы для вещества, то, на основании закона сохранения массы, в стационарном режиме массовый расход газа (пара) через любое сечение канала будет постоянной величиной, т.е. G=const. Тогда (7.10) запишется в виде, который часто называют уравнением неразрывностиили сплошности:
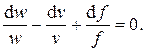 (7.11)
(7.11)
Сопло и диффузор
Запишем I закон термодинамики при принятых выше допущениях с точки зрения неподвижного наблюдателя (7.8) и с точки зрения наблюдателя, жёстко связанного с системой:
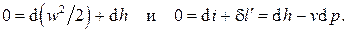 (7.12)
(7.12)
Поскольку оба эти выражения описывают одну и ту же систему, из их сравнения находим
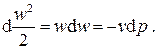 (7.13)
(7.13)
На основании этого выражения можно ввести два определения:
1) сопло – канал, предназначенный для ускорения потока (dw>0) за счёт уменьшения давления (dp<0);
2) диффузор – канал, предназначенный для увеличения давления (dp>0) за счёт торможения потока (dw<0).
| Р8.Т2 | Расчёт течения газов и паров в каналах. | 1.2 часа |
Первый закон термодинамики в форме (7.8) легко интегрируется, так как входящие в него дифференциалы являются полными: 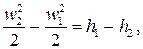 причём этот результат справедлив как для обратимого течения, так и для необратимого. Обычно интересуются скоростью w2потока в выходном сечении канала, для которой имеем
причём этот результат справедлив как для обратимого течения, так и для необратимого. Обычно интересуются скоростью w2потока в выходном сечении канала, для которой имеем
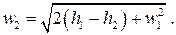 (7.14)
(7.14)
Мы будем для определённости рассматривать только сопла, в которых скорость на выходе w2значительно превышает скорость на входе w1, так что под корнем в (7.14) можно пренебречь вторым слагаемым, т.е. для сопел скорость истечения может рассчитываться по формуле
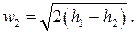 (7.15)
(7.15)
Из (7.12) следует также, что разность энтальпий при течении в адиабатических соплах равна полезной внешней работе потока, откуда
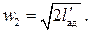 (7.16)
(7.16)
В случае идеального газа на основании выражения для полезной внешней работы адиабатического процесса (3.33) получаем
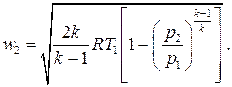 (7.17)
(7.17)
Массовый расход газа при известной скорости в выходном сечении находится на основании определения (7.9)
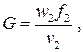
где удельный объём в выходном сечении находится из условия адиабатичности процесса, т.е.
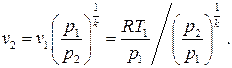 (7.18)
(7.18)
С учётом этого выражение для массового расхода идеального газа принимает вид
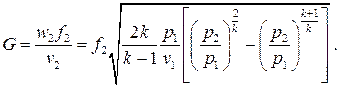 (7.19)
(7.19)
Построим графики зависимости скорости истечения газа из сопла w2 и массового расхода газа G от отношения давлений за соплом p2 и перед соплом p1, для чего введём обозначение
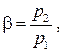 (7.20)
(7.20)
причём β может изменяться в пределах от 0 до 1, так как давление газа на выходе p2 для сопел по определению меньше давления на входе p1 и оба они положительны.
Для упрощения графического представления введём также безразмерные скорость истечения и массовый расход с помощью равенств
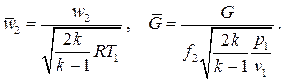 (7.21)
(7.21)
Тогда для безразмерных скорости истечения и расхода получаем следующие выражения:
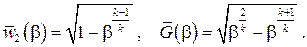 (7.22)
(7.22)
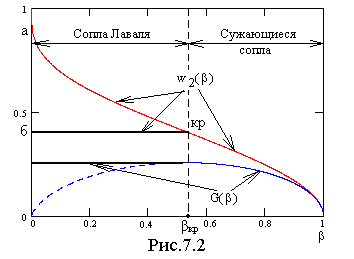 |
Графики этих функций показаны на рис.7.2.
Сравнение с экспериментом показывает, что формулы (7.22) для скорости и расхода (или (7.17) и (7.19) для размерных величин) справедливы в интервале значений отношения давлений β от некоторого критического βкр до единицы, причём при 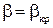 массовый расход G принимает максимальное значение. В интервале же
массовый расход G принимает максимальное значение. В интервале же 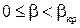 массовый расход не зависит от отношения давлений β и оказывается равным Gmax, в то время как теория даёт ниспадающую до нуля ветвь при уменьшении β до нуля (на рисунке показана штриховой линией). Скорость потока в этом же интервале β может вести себя двояким образом: либо возрастать с уменьшением отношения давлений, что описывается теоретической формулой (7.17), либо оставаться постоянной и равной скорости при критическом отношении давлений βкр. Вычислим βкр из условия максимума массового расхода:
массовый расход не зависит от отношения давлений β и оказывается равным Gmax, в то время как теория даёт ниспадающую до нуля ветвь при уменьшении β до нуля (на рисунке показана штриховой линией). Скорость потока в этом же интервале β может вести себя двояким образом: либо возрастать с уменьшением отношения давлений, что описывается теоретической формулой (7.17), либо оставаться постоянной и равной скорости при критическом отношении давлений βкр. Вычислим βкр из условия максимума массового расхода:
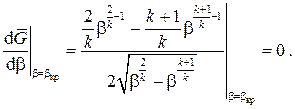
Отсюда, приравнивая числитель нулю при β =βкр, получаем
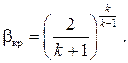 (7.23)
(7.23)
Таким образом, критическое отношение давлений при адиабатном течении идеального газа в соплах зависит только от его показателя адиабаты, т.е. от числа атомов в молекулах, составляющих газ. Значения βкр представим в табл.7.1, которая является расширением табл.2.1. Здесь же приведено ориентировочное значение критического отношения давлений для водяного пара вблизи верхней пограничной кривой, которое может быть использовано для практических расчётов.
Таблица 7.1
| Газ | 1 – атомный | 2 – атомный | 3 – и более атомный | Водяной пар |
| Число степеней свободы f | ||||
| Показатель адиабаты k | 1.67 | 1.40 | 1.33 | – |
| Критическое отношение давлений βкр | 0.487 | 0.528 | 0.540 | 0.546 |
Для выяснения физического смысла расхождения теории с экспериментом в интервале значений отношения давлений 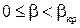 , подставим β = βкр (7.23) в выражение для скорости истечения из адиабатического сопла (7.17) :
, подставим β = βкр (7.23) в выражение для скорости истечения из адиабатического сопла (7.17) :
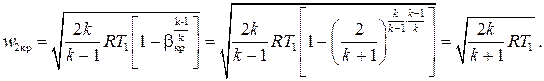

С другой стороны, из условия адиабатичности процесса течения имеем
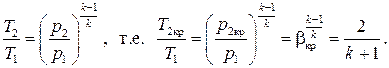
Отсюда находим, что скорость истечения газа при критическом отношении давлений определяется выражением
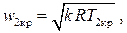 (7.24)
(7.24)
а это есть не что иное, как скорость звука в газах, т.е. скорость распространения малых возмущений давления, плотности и т.д. Таким образом, аномалия в поведении скорости потока в адиабатическом сопле связана с переходом от дозвукового режима течения к сверхзвуковому.
Дата добавления: 2015-12-22; просмотров: 3837;
