Исследование политропных процессов

Каждому политропному процессу отвечает свой собственный закон распределения энергии и свое собственное значение n, т. е. величина n и закон распределения энергии в политропном процессе взаимосвязаны. Отсюда и возникает возможность по величине n судить о характере распределения энергии в процессе. Наметим три характерные группы политроп:

1. показатель политропы изменяется в пределах 1 < n < k;

2. показатель политропы изменяется в пределах -¥ < n < 1;

3. показатель политропы изменяется в пределах +¥ > n > k.

Покажем, что у каждой из намеченных групп политроп имеется свой собственный закон распределения энергии, который можно легко определить в результате следующего анализа.

Рассмотрим вначале расположение всевозможных политропных процессов по отношению к адиабатному процессу (рис. 4.4).

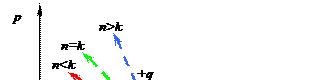В рu- координатах все политропные процессы расположены или выше или ниже адиабаты. Если зафиксировать для всех политроп расширения некоторой объем, то из элементарных рассуждений следует, что если в данном процессе (n > k) при объеме u давление упало по отношению к адиабатному, в котором внешнее тепло не участвует (q = 0), то это может быть только за счет дополнительного отвода тепла (q < 0) в этом процессе. Наоборот, если при расширении к моменту наступления объема u, давление в политропном процессе (n < k) повысилось по отношению к адиабатному (q = 0), то это может произойти только за счет подвода тепла в этом процессе (q > 0). К аналогичным результатам можно прийти, если рассмотреть соответствующие политропы сжатия.

Следовательно, адиабата разделяет всевозможные политропы на две группы: первая группа политроп в рu- координатах, расположенных выше адиабаты, идет с подводом тепла (+q), вторая группа политроп, расположенных ниже адиабаты, идет с отводом тепла (-q), независимо от того, идут ли процессы сжатия или расширения. В Тs- координатах, процессы, расположенные вправо от адиабаты (с увеличением энтропии), идут с подводом тепла, влево от адиабаты (с уменьшением энтропии) идут с отводом тепла.

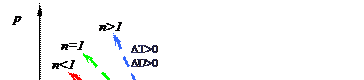Рассмотрим расположение всевозможных политроп по отношению к изотерме (рис. 4.5).

Если опять зафиксировать в ходе процессов расширения какой-то объем υ, то, сопоставляя политропные процессы с изотермическими (n=1, T=const), можно сделать следующие выводы. Если в политропическом процессе расширения к моменту наступления υ давление оказалось выше, чем в изотермическом, это может произойти только в результате повышения температуры газа, т. к. в изотермическом процессе расширения теплота сообщается газу, но Т = const. Так как температура в этих процессах увеличивается, то и внутренняя энергия в этих процессах возрастает. Наоборот, если давление в политропном процессе лежит ниже значения давлений изотермического процесса, то это означает, что эти процессы расширения сопровождаются понижением температуры и уменьшением внутренней энергии газа. Аналогичные результаты получаются, если рассмотреть соответствующие политропы сжатия.

Итак, изотерма в pυ- и Ts- координатах делит всевозможные политропы на две группы:

- первая группа политроп, лежащая выше изотермы, идет с увеличением u (∆u > 0) и ростом Т (∆T > 0).

- вторая группа политроп, лежащая ниже изотермы, идет с уменьшением u (∆u < 0) и понижением Т (∆T < 0), .

Это правило справедливо для всех процессов как сжатия, так и расширения.

Воспользовавшись данной системой анализа, определим закон распределения энергии в каждой из намеченных групп.

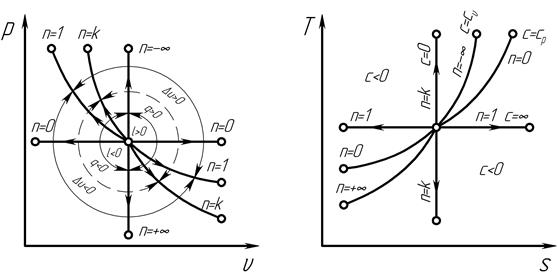
Рис. 4.6. Политропные процессы

Первая группа политропных процессов.

К этой группе относятся процессы (рис. 4.6) у которых 1 < n < k , графики этих процессов располагаются между изотермой и адиабатой. Процессы этой группы в случае расширения газа осуществляются с подводом тепла (процессы расположены выше адиабаты) и с уменьшением внутренней энергии газа (процессы расположены ниже изотермы), т. е. согласно схеме, представленной на рис. 4.7.

Коэффициент распределения теплоты ψ у этой группы процессов будет отрицательным. Это свидетельствует о том, что тепло q и изменение внутренней энергии ∆u в этих процессах имеют разные знаки.

При увеличении показателя n этой группы процессов закон распределения энергии остается постоянным, но усиливается роль в процессе внутренней энергии и уменьшается роль теплоты.

Теплоемкость газа в политропных процессах этой группы, вычисляемая по формуле:

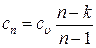
будет величиной отрицательной. Физически это означает, что в этих процессах, несмотря на сообщение газу теплоты, его внутренняя энергия, а с ней температура уменьшаются.

Вторая группа политропных процессов.

К этой группе относятся процессы, у которых -∞ < n < 1 (рис. 4.6). Графики политропных процессов второй группы располагаются между изохорой и изотермой. В процессах этой группы расширение газа осуществляется с подводом теплоты (процессы расположены выше адиабаты) и увеличением внутренней энергии газа (процессы расположены над изотермой), т.е. согласно схеме, представленной на рис.4.8.

Часть теплоты, идущей на увеличение внутренней энергии газа (ψ) величина положительная. С увеличением n у процессов этой группы закон распределения энергии сохраняется, но при этом уменьшается доля теплоты, идущей на увеличение ∆u, и увеличивается доля теплоты, идущей на l. Теплоемкость газа в процессах этой группы будет величиной положительной.

Третья группа политропных процессов.

К этой группе принадлежат процессы, в которых +∞ > n > k графики этих процессов лежат между адиабатой и изохорой.

Процессы этой группы в случае расширения газа осуществляются с уменьшением внутренней энергии (процессы расположены ниже изотермы) и отдачей теплоты в холодильник (процессы расположены ниже адиабаты), т.е. согласно схеме, представленной на рис. 4.9.

С увеличением показателя n этой группы процессов закон распределения энергии сохраняется, но увеличивается доля теплоты (за счет уменьшения внутренней энергии), отдаваемая в холодильник, и уменьшается доля теплоты, идущая на работу.

Теплоемкость газа этой группы процессов будет величиной положительной. Коэффициент распределения теплоты ψ у этой группы процессов величина положительная.

Лекция № 5

Тема: «ТЕРМОДИНАМИКА РЕАЛЬНЫХ ГАЗОВ И ПАРОВ» (2 часа)

1 ПЛАН

1. Основные понятия и определения.

2. Особенности р, u - диаграммы водяного пара.

3. Основные параметры водяного пара.

4. Ts – диаграмма водяного пара.

5. hs – диаграмма водяного пара.

2. ЛИТЕРАТУРА

Основная литература

1. Амерханов Р.А., Драганов Б.Х. Теплотехника. - М.: Энергоатомиздат, 2006. – 432 с.

2. Круглов Г.А., Булгакова Р.И., Круглова Е.С. Теплотехника. – СПб.: Издательство «Лань», 2010. – 208 с.

Дополнительная литература

1. Теплотехника. /А.П. Баскаков, Б.В. Берг и др. – М.: Энергатомиздат, 1991. – 224 с.

2. Техническая термодинамика. / Кириллин В.А., Сычев В.В., Шейндлин А.Е. – М.: Издательский дом МЭИ, 2008. – 496 с.

Основные понятия и определения

Водяной пар широко используется во всех отраслях техники, и прежде всего в теплоэнергетике, где он является основным рабочим телом.

Процесс превращения вещества из жидкого состояния в газообразное называется парообразованием. Испарением называется парообразование, которое происходит всегда при любой температуре со свободной поверхности жидкости или твердого тела. Процесс кипения заключается в том, что если к жидкости подводить теплоту, то при некоторой температуре, зависящей от физических свойств рабочего тела и давления, наступает процесс парообразования как на свободной поверхности жидкости, так и внутри ее.

Переход вещества из газообразного состояния в жидкое называется конденсацией. Жидкость, полученная при конденсации пара, называется конденсатом.

Процессы парообразования и конденсации протекают при постоянной температуре, если при этом не меняется давление.

Если парообразование жидкости происходит в неограниченном пространстве, то вся она может превратиться в пар. Если же парообразование жидкости происходит в закрытом сосуде, то при определенных условиях наступает состояние насыщения.

Насыщенным называется пар, находящийся в термическом и динамическом равновесии с жидкостью, из которой он образуется. Динамическое равновесие заключается в том, что количество молекул, вылетающих из воды в паровое пространство, равно количеству молекул, конденсирующихся на ее поверхности. Температура насыщенного пара есть монотонно возрастающая функция его давления.

При увеличении объема над поверхностью жидкости, имеющей температуру насыщения, некоторое количество жидкости переходит в пар, при уменьшении объема «излишний» пар снова переходит в жидкость, но в обоих случаях давление пара остается постоянным.

Насыщенный пар, в котором отсутствуют взвешенные частицы жидкой фазы, называется сухим насыщенным паром. Состояние сухого насыщенного пара задается одним параметром – давлением, или удельным объемом, или температурой.

Двухфазная смесь, представляющая собой пар со взвешенными в нем капельками жидкости, называется влажным насыщенным паром. Массовая доля сухого насыщенного пара во влажном называется степенью сухости и обозначается буквой х:

.

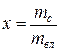Массовая доля кипящей жидкости во влажном паре, равная (1 – х), называется степенью влажности. Для кипящей жидкости х = 0, а для сухого насыщенного пара х = 1, следовательно, степень сухости может меняться только в пределах от 0 до 1. Состояние влажного пара задается двумя параметрами: давлением (или температурой насыщения t_s, определяющей это давление) и степенью сухости пара.

Если сухому насыщенному пару сообщить некоторое количество теплоты при постоянном давлении, то температура его будет возрастать и образуется перегретый пар. Перегретым называется пар, температура которого превышает температуру насыщения пара того же давления. Перегретый пар является не насыщенным, так как при данном давлении удельный объем перегретого пара больше удельного объема сухого насыщенного пара, а плотность меньше. Он по своим физическим свойствам приближается к газу и тем ближе, чем выше степень перегрева. Состояние перегретого пара, как и любого газа, задается двумя любыми независимыми параметрами.

2. Особенности рu - диаграммы водяного пара

Рассмотрим рu - диаграмму системы, состоящей из жидкости и пара (рис. 5.1).

Пусть вода при T = 273 К и некотором давлении р занимает объем u₀ (отрезок 0-1). Если при постоянном давлении сообщить воде некоторое количество теплоты q_ж, то ее температура будет повышаться, а удельный объем увеличиваться. При некоторой температуре Т_кип вода закипает, а ее удельный объем u¢ в точке 2 достигнет при данном давлении максимального значения. Следовательно, процесс 1-2 – нагрев воды при постоянном давлении p = const.

В случае дальнейшего подвода теплоты при постоянном давлении, например в количестве r, начнется процесс парообразования. При этом количество воды будет уменьшаться, количество пара увеличиваться. В момент окончания парообразования в точке 3 пар будет сухим насыщенным. Удельный объем сухого насыщенного пара обозначается u². Следовательно, процесс 2-3 – процесс парообразования при постоянном давлении и постоянной температуре p, Т = const.

Если к сухому насыщенному пару дальше подводить теплоту при постоянном давлении, например, в количестве q_пер, то температура и объем его будут увеличиваться и пар из сухого насыщенного перейдет в перегретый (точка 4). Следовательно, процесс 3-4 – процесс перегрева пара при постоянном давлении p = const.

Если процесс парообразования будем осуществлять при высоком давлении (р¢ > р), то объем холодной воды u₀ незначительно уменьшится (практически остается постоянным), объем кипящей воды – увеличится, а объем сухого насыщенного пара уменьшится по сравнению с исходным, т. е. при возрастании давления разность u¢ – u₀ (или отрезок 1-2) увеличивается, а разность u² – u¢ (или отрезок 2-3) – уменьшается. Если процесс парообразования проведем при давлении меньше первоначально рассмотренного (р² < р), то в этом случае объем кипящей воды уменьшится, а объем сухого насыщенного пара увеличится по сравнению с исходным, т. е. при уменьшении давления разность u¢ – u₀ (или отрезок 1-2), уменьшается, а разность u² – u¢ (или отрезок 2-3) увеличивается.

Таким образом, на рu - диаграмме водяного пара получим три характерные кривые. Кривая ЕА представляет собой зависимость удельного объема воды от давления при T = 273 К. Кривая АК выражает зависимость удельного объема кипящей воды от давления, и называется пограничной кривой жидкости. Характеристикой кривой АК является степень сухости х = 0. Кривая КВ выражает зависимость удельного объема сухого насыщенного пара от давления, которая называется пограничной кривой пара. Характеристикой кривой КВ является степень сухости х = 1.

Обе кривые АК и ВК делят диаграмму на три части. Влево от пограничной кривой жидкости АК до нулевой изотермы располагается область жидкости. Между кривыми АК и ВК располагается двухфазная система, состоящая из смеси воды и сухого пара. Вправо от ВК и вверх до точки К располагается область перегретого пара или газообразного состояния тела. Кривые АК и ВК сходятся в одной точке К, которая называется критической точкой.

Критическая точка является конечной точкой фазового перехода жидкость-пар. Выше критической точки существование вещества в двухфазном состоянии невозможно. В этой точке различия между жидкостью и паром исчезают. Для воды параметры критической точки К составляют:

р_кр = 221,29×10⁵ Па; t_кр = 374,15 °С; u_кр = 0,00326 м³/кг.

Наименьшим давлением, при котором еще возможно равновесие воды и насыщенного пара, является давление, соответствующее тройной точке (точка А). Тройная точка это то единственное состояние, в котором могут одновременно находиться в равновесии пар, вода и лед. Параметры тройной точки для воды: р₀ = 611 Па; t₀ = 0,01 °С; u₀ = 0,00100 м³/кг. Процесс парообразования, происходящий при абсолютном давлении р₀ = 611 Па показан на диаграмме изобарой АВ, которая совпадает с осью абсцисс.