Политропные процессы идеальных газов

Политропным процессом называется такой процесс изменения состояния рабочего тела, при котором во внутреннюю энергию в течение всего процесса, превращается одна и та же доля количества теплоты.

Из определения политропного процесса следует, что основные термодинамические процессы – изохорный, изобарный, изотермический и адиабатный являются частными случаями политропных процессов.

Уравнение политропного процесса выводится на основании уравнения первого закона термодинамики:

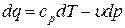или .

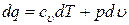Количество теплоты, участвующее в политропном процессе, может быть выражено произведением теплоемкости на разность температур в конечном и начальном состояниях:

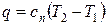или .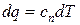

Тогда

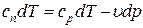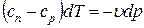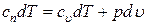; Þ ;

; Þ .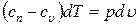

Разделив первое уравнение на второе, получим:

,

,

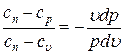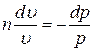где 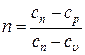- показатель политропы.

По аналогии с выражением для адиабатного процесса, находим:

.

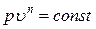Показатель политропы n может принимать любое численное значение в пределах от - ¥ до + ¥, но для данного процесса он является величиной постоянной.

Поскольку уравнение политропы отличается от уравнения адиабаты только величиной показателя n, то, очевидно, все соотношения между основными параметрами могут быть представлены формулами, аналогичными адиабатному процессу:

; ; .

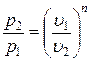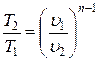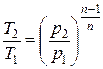Теплоемкость политропного процесса определяется из формулы:

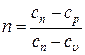Þ .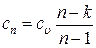

Следовательно, теплоемкость идеального газа при осуществлении политропного процесса зависит от показателя политропы.

Уравнение работы изменения объема, совершаемой телом при политропном процессе, имеет аналогичный вид с уравнениями работы в адиабатном процессе:

;

; ; .

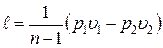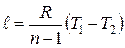
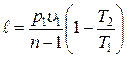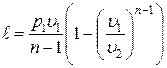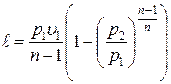Изменение внутренней энергии газа определяется по той же формуле, что и для всех процессов:

.

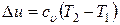Количество подведенной (или отведенной) в процессе теплоты определяется по формуле:

.

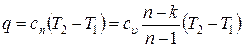Изменение энтропии газа в политропном процессе находим по выражению:

,

.

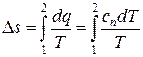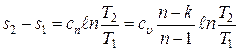Полученное выражение показывает, что в общем случае политропа в Ts – диаграмме будет некоторой кривой линией, вид и положение которой зависит от величины показателя политропы n.