Кибернетический подход в логистике
Кибернетика –наука об общих принципах управления, понимаемого как организация целенаправленных действий путем переработки информации.
Объектом ее (кибернетики) изучения являются динамические системы.
Предметом – информационные процессы, связанные с управлением динамическими системами.
Кибернетическая система – «множество взаимосвязанных объектов, называемых элементами системы, способных воспринимать, запоминать и перерабатывать информацию, а также обмениваться информацией» (Глушков В.М.). Кибернетика рассматривает системы независимо от природы входящих в них элементов. Кибернетическим системам свойственны самоорганизация и самообучение.
Системы с управлением обладают также свойством целеустремленности. Такие системы представляют в виде двух подсистем – управляющей и управляемой, или объекта управления. Они находятся во взаимодействии, т.е. не только управляющая система передает информацию (команды, сигналы) управляемому объекту, но и обратно поступает информация о состоянии последнего. Поэтому важнейшим видом кибернетических систем являются системы с обратной связью.
Экономическая кибернетика –приложение общих законов кибернетики к изучению экономических явлений и управлению экономическими процессами. Экономическая кибернетика является основой автоматизации управления, научно-теоретической базой разработки АСУ в народном хозяйстве. При этом она исходит из того, что управление есть процесс переработки информации; принятое решение – новая информация, которой руководствуются все те, кого это решение касается.
Логистическая система является целенаправленной, управляемой, и относится к категории кибернетических систем.
В кибернетическом подходе, способ представления логистических моделей опирается на положение о том, что всем объектам производственно-коммерческой деятельности присущи движение, изменение и процесс. Как уже отмечалось, основным отличительным понятием кибернетики является обратная связь. Поэтому, логистическую систему можно представить в виде, так называемого «черного ящика» со входом и выходом, а также обратной связью через регулятор:
| Н |
| Т |
| Вход Х Δх |
| Выход У Δу |
Рис. 4. Контур управления с обратной связью
Где: Н – регулируемая система (процесс);
Х = (х1,х2,…,хm) – вектор входа;
У = (у1,у2,…,уn) – вектор выхода.
В регулируемой системе Н происходит преобразование состояния входа Х в состояние выхода У, математически это выглядит: У = НХ.
Как показывает блочная схема, текущее состояние выхода У после сопоставления с эталонным или заданным его значение передается на вход регулятора Т, который преобразует его в состояние своего выхода Δх. Состояние выхода регулятора прибавляется к значению состояния входа Х – системы Н. В конечном итоге состояние входа системы Н есть Х + Δх. Поправка на входе системы Н зависит от состояния ее выхода У. Обозначим через 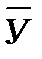 заданное значение, т.е. желаемую норму состояния выхода регулируемой системы. Соответствующая настройка регулятора Т заключается в том, чтобы поправка Δх вызвала выравнивание всякого отклонения Δу от заданного значения
заданное значение, т.е. желаемую норму состояния выхода регулируемой системы. Соответствующая настройка регулятора Т заключается в том, чтобы поправка Δх вызвала выравнивание всякого отклонения Δу от заданного значения 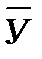 и привела состояние выхода регулируемой системы к заданной норме, т.е. Δу =
и привела состояние выхода регулируемой системы к заданной норме, т.е. Δу = 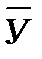 -У→ 0. Можно произвести расчет, определяющий численные показатели описанной таким образом обратной связи. Допустим вначале, что в регулируемой системе происходит прямое преобразование, состоящее в умножении состояния входа на действительное число Н; тогда У=НХ.
-У→ 0. Можно произвести расчет, определяющий численные показатели описанной таким образом обратной связи. Допустим вначале, что в регулируемой системе происходит прямое преобразование, состоящее в умножении состояния входа на действительное число Н; тогда У=НХ.
Пропорциональное преобразование называют усилением, если Н>1, или ослаблением, если Н<1. В этих случаях системы, в которых происходит пропорциональное преобразование, называют соответственно, усилителями или ослабителями. Показатель Н=У/Х называется пропускной способностью системы.
Дата добавления: 2015-12-22; просмотров: 956;
