Матрица попарных сравнений для уровня 3
| A1 | К | L | М | A2 | К | L | М |
| K | К | ||||||
| L | L | ||||||
| М | М | ||||||
| А3 | K | L | М | A4 | K | L | М |
| К | K | ||||||
| L | L | ||||||
| М | М |
При сравнении элементов К и L задают вопросы:
какой из них важнее или имеет большее воздействие?
какой из них более вероятен?
какой из них предпочтительнее?
Отметим, что клетки этих матриц не заполнены, они оставлены для оценок или суждений об относительной важности сравниваемых отдельных предметов, по отношению к цели, или критерию (фактору). Если существует шкала сравнений, т.е. имеется некоторый способ измерения, то данные могут использоваться для проведения сравнений, иначе клетки заполняются оценками, полученными в результате субъективных, но продуманных суждений индивидуума или группы, решающей проблему.
Синтез приоритетов
Из группы матриц парных сравнений формируется набор локальных приоритетов, которые выражают относительное влияние множества элементов на элемент примыкающего сверху уровня.
Порядок формирования локальных приоритетов следующий.
Вычисляем собственные вектора:

Таким образом, компонента собственно вектора первой строки равна
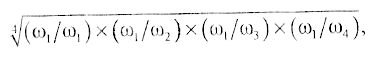
компонента собственного вектора третьей строки равна
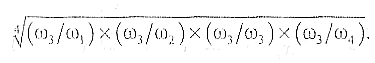
После того как компоненты собственного вектора получены для всех п строк, их возможно использовать для дальнейших вычислений:

Когда матрица имеет такой вид, получается, что в действительности х1, х2, х3 и x4 есть не что иное, как w1, w2, w3, ..., wп соответственно. Из отношений wi/wj определим каждую компоненту w. Важно отметить, что в матрице суждений нет отношений в виде wi/wj, а имеются только целые числа или их обратные величины из шкалы.
Синтез глобальных приоритетов
Приоритеты синтезируются, начиная со второго уровня вниз. Порядок синтеза состоит в следующем. Локальные приоритеты перемножаются на приоритеты соответствующего фактора (критерия) на вышестоящем уровне и суммируются по каждому элементу в соответствии с факторами (критериями), на которые воздействует этот элемент.
Глобальные приоритеты позволяют путем сравнения принять решение.
Для выполнения условий согласованности в матрицах попарных сравнений используются обратные величины aij = 1/аij вместо традиционно используемых при построении интервальных шкал величин aij = - аij.
Индекс согласованности (ИС) может быть получен следующим образом. Сначала суммируется каждый столбец суждений, затем сумма первого столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца умножается на величину первой компоненты нормализованного вектора приоритетов, сумма второго столбца — на вторую компоненту и т.д. Затем полученные числа суммируются. Таким образом можно получить величину, обозначаемую lmax. Для индекса согласованности имеем:
ИС = (lmax - n)/(n - 1),
где п — число сравниваемых элементов.
Для обратносимметричной матрицы всегда lтах ³ п. В табл. 7.19 даны средние согласованности для матриц разного порядка.
Таблица 7.19.
Дата добавления: 2015-12-22; просмотров: 1566;
