Показатель связи распределения нагрузок

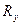Формулы (8) преобразования показателей разброса нагрузок и при повороте системы координат показывают, что эти показатели в новой системе координат выражаются через исходные показатели и третью новую величину , смысл которой раскрывается при помощи следующей геометрической интерпретации: наборы произведений

(23)

будем рассматривать как векторы в n-мерном евклидовом пространстве. Тогда показатели разбросов и 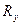по осям могут быть интерпретированы как квадраты длин этих векторов. Векторы эти в рассматриваемом пространстве в зависимости от распределения нагрузок приёмников в группе имеют такое взаимное расположение, которое определяется косинусом угла между ними

(24)

Существование этой величины обосновано известным неравенством Коши-Буняковского, которое для данной задачи имеет вид:

(25)

Знак равенства в этом соотношении имеет место в том и только в том случае, когда векторы и параллельны

(26)

т.е. когда приёмники электроэнергии расположены на отрезке прямой , проходящей через точку ( 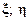). В этом случае в зависимости от знака коэффициента пропорциональности. При уменьшении от 1 до нуля при одних и тех же длинах векторов и величина убывает до нуля. Расположение нагрузок в группе изменяется: они заполняют некоторую область, и в пределе, когда , векторы и ортогональны. Этот факт будем интерпретировать как уменьшение линейной связи распределения нагрузок вдоль отрезка прямой, а величину

(27)

как показатель связи распределения нагрузок. Эта величина обладает свойством

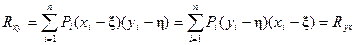(28)

т.е. она не изменяется при перестановке сомножителей и . При повороте системы координат на угол показатель связи преобразуется по формуле

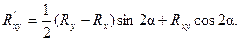(29)

Следовательно, существуют два таких взаимно перпендикулярных направления, в которых показатель связи достигает как наибольшего, так и наименьшего значений.