Показатели характеристических свойств группы приёмников
Выразим через независимые инварианты 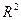 и
и 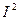 тензора (30) показатели некоторых характеристических свойств, описывающих любую группу приёмников. Описать группу приёмников при помощи показателей характеристических свойств – это значит получить необходимую информацию о закономерностях распределения нагрузок и геометрии взаимного расположения приёмников в группе относительно возможного центра их питания. Такая информация приобретает важное значение при решении задач автоматизированного проектирования систем электроснабжения промышленных предприятий. Дело в том, что в процессе автоматизированного формирования и отбора вариантов систем электроснабжения возникает необходимость оценивать эти варианты, не прибегая к фиксации их на планах. Такая задача может быть решена только с помощью формализованных показателей, раскрывающих свойства групп приёмников, распределенных по источникам питания, а следовательно, и самих вариантов, от которых зависят технико-экономические показатели проекта. Простейшие показатели характеристических свойств группы приёмников – это центр электрических нагрузок и показатели разброса нагрузок вдоль осей координат и относительно произвольной точки (
тензора (30) показатели некоторых характеристических свойств, описывающих любую группу приёмников. Описать группу приёмников при помощи показателей характеристических свойств – это значит получить необходимую информацию о закономерностях распределения нагрузок и геометрии взаимного расположения приёмников в группе относительно возможного центра их питания. Такая информация приобретает важное значение при решении задач автоматизированного проектирования систем электроснабжения промышленных предприятий. Дело в том, что в процессе автоматизированного формирования и отбора вариантов систем электроснабжения возникает необходимость оценивать эти варианты, не прибегая к фиксации их на планах. Такая задача может быть решена только с помощью формализованных показателей, раскрывающих свойства групп приёмников, распределенных по источникам питания, а следовательно, и самих вариантов, от которых зависят технико-экономические показатели проекта. Простейшие показатели характеристических свойств группы приёмников – это центр электрических нагрузок и показатели разброса нагрузок вдоль осей координат и относительно произвольной точки ( 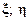 ) и ЦЭН. Все эти показатели связаны с инвариантом
) и ЦЭН. Все эти показатели связаны с инвариантом 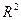 тензора (30). Теперь стоит задача описать размеры областей распределения нагрузок и расположения самих приёмников в группе. Показатель размера области распределения нагрузок мы получим, если инвариант
тензора (30). Теперь стоит задача описать размеры областей распределения нагрузок и расположения самих приёмников в группе. Показатель размера области распределения нагрузок мы получим, если инвариант 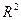 разделим на суммарную нагрузку приёмников группы
разделим на суммарную нагрузку приёмников группы
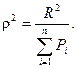 (36)
(36)
Этот показатель представляет собой квадрат средних расстояний, взвешенных по нагрузкам мест расположения приемников в группе от точки ( 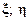 ), относительно которой вычислен разброс
), относительно которой вычислен разброс 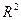 , до места расположения приёмников. Этот показатель зависит от выбора точки (
, до места расположения приёмников. Этот показатель зависит от выбора точки ( 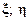 ). Наименьшее значение он принимает, когда разброс
). Наименьшее значение он принимает, когда разброс 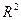 вычислен относительно центра электрических нагрузок. Показатель размера области распределения нагрузок остается неизменным при повороте осей системы координат. Следовательно, он является инвариантом тензора (30). Показатель (36) имеет размерность квадрата длины. Для наглядной характеристики размера области распределения нагрузок удобнее пользоваться показателем, размерность которого совпадает с длиной. Для этого из (36) извлечем корень квадратный
вычислен относительно центра электрических нагрузок. Показатель размера области распределения нагрузок остается неизменным при повороте осей системы координат. Следовательно, он является инвариантом тензора (30). Показатель (36) имеет размерность квадрата длины. Для наглядной характеристики размера области распределения нагрузок удобнее пользоваться показателем, размерность которого совпадает с длиной. Для этого из (36) извлечем корень квадратный
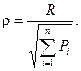 (36а)
(36а)
Чтобы получить геометрические характеристики расположения приёмников в группе, в (11) и (36), (36а) положим все нагрузки приёмников равными единице, тогда получим формулы для расчётов:
а) геометрического центра расположения приёмников в группе
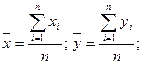 (36б)
(36б)
б) среднего квадрата размера области расположения приёмников в группе относительно точки (  )
)
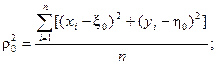
в) среднего размера области расположения приемников в группе относительно той же точки
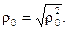
Эти показатели необходимы при разбиении некоторого множества приёмников на группы для того, чтобы потери мощности в каждой группе были меньше заданных. Для этого надо собрать такие группы, чтобы 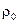 не превышало допустимых значений. Кроме того, эти показатели войдут в другие показатели, один из которых рассмотрен ниже.
не превышало допустимых значений. Кроме того, эти показатели войдут в другие показатели, один из которых рассмотрен ниже.
Для группы приёмников, изображенной на рис. 5, ЦЭН и геометрический центр (36б) совпадают. Но стоит изменить нагрузку или место расположения любого приёмника, как сразу же происходит смещение одного центра относительно другого. Следовательно, всякие неравномерности распределения приёмников и их нагрузок в группе влекут за собой смещение ЦЭН относительно геометрического центра. Такое свойство называют асимметрией распределения нагрузок относительно ЦЭН, и измеряют его при помощи следующей безразмерной величины:
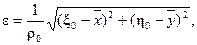 (37)
(37)
которую будем называют показателем асимметрии распределения нагрузок относительно геометрического центра. Если ЦЭН совмещен с геометрическим центром, то 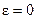 , распределение нагрузок симметричное. При смещении ЦЭН на границу участка области расположения приёмников показатель асимметрии
, распределение нагрузок симметричное. При смещении ЦЭН на границу участка области расположения приёмников показатель асимметрии 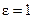 .
.
Из (8) видно, что при повороте системы координат на угол 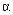 показатели разброса нагрузок
показатели разброса нагрузок  и
и 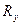 вдоль осей системы координат изменяют свои значения, следовательно, найдутся два таких направления, в одном из которых показатель разброса нагрузок будет наибольшим, а в другом – наименьшим. Поиск таких направлений осуществляется исследованием на экстремум функции (8) разброса нагрузок в зависимости от угла
вдоль осей системы координат изменяют свои значения, следовательно, найдутся два таких направления, в одном из которых показатель разброса нагрузок будет наибольшим, а в другом – наименьшим. Поиск таких направлений осуществляется исследованием на экстремум функции (8) разброса нагрузок в зависимости от угла 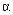 поворота осей системы координат. Производные первого порядка от той и другой функции, например
поворота осей системы координат. Производные первого порядка от той и другой функции, например
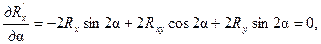 (38)
(38)
приводят к одному и тому же условию, определяющему эти направления,
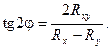 (39)
(39)
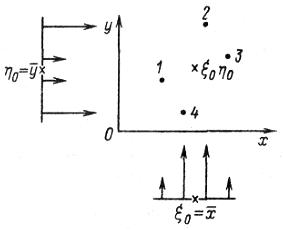
Рис. 5. Группа приёмников, использованная для иллюстрации характеристики 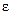
Каждому значению тангенса соответствуют два угла
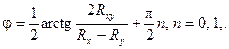 (39а)
(39а)
отличающиеся друг от друга на 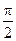 .
.
Один из этих углов определяет направление наибольшего разброса нагрузок, а другой – наименьшего разброса нагрузок приёмников в группе. Эти направления будем называть главными осями разброса нагрузок. Для однозначного определения угла, составленного осью 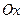 и главной осью наибольшего разброса нагрузок, руководствуются правилом: если
и главной осью наибольшего разброса нагрузок, руководствуются правилом: если 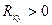 и
и 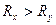 или
или  и
и 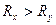 , то в этой формуле следует положить
, то в этой формуле следует положить 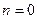 ; если же
; если же  и
и 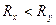 или
или 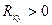 и
и 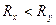 , то
, то 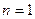 . При повороте системы координат на этот угол ось
. При повороте системы координат на этот угол ось 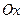 будет совмещена с осью наибольшего разброса. Легко убедиться, что в главных осях разброса нагрузок показатель связи
будет совмещена с осью наибольшего разброса. Легко убедиться, что в главных осях разброса нагрузок показатель связи 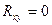 . Для этого нужно в третью формулу из (31) подставить значения
. Для этого нужно в третью формулу из (31) подставить значения 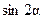 и
и 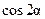 , найденные из (39).
, найденные из (39).
Рассмотрим свойства второго независимого инварианта 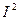 , определённого по (35). Сопоставим изменение
, определённого по (35). Сопоставим изменение  ,
, 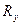 и
и 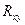 в правой части формулы (35б) с поведением уравнения (33) эллипса тензора. Если
в правой части формулы (35б) с поведением уравнения (33) эллипса тензора. Если 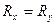 и
и 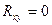 , то уравнение эллипса вырождается в уравнение окружности
, то уравнение эллипса вырождается в уравнение окружности
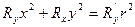 . (40)
. (40)
Следовательно, область разброса нагрузок группы приемников – круг, и по любым направлениям разбросы нагрузок одинаковы. Предполагая, что одна компонента тензора равна, например, 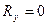 , из формулы
, из формулы
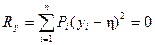 (41)
(41)
получим, что 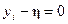 , для всех
, для всех 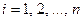 номеров приёмников электроэнергии момент связи
номеров приёмников электроэнергии момент связи 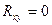 и уравнение эллипса тензора вырождается в пару уравнений прямых
и уравнение эллипса тензора вырождается в пару уравнений прямых
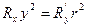 . (42)
. (42)
параллельных оси 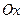 . В направлении одной из них разброс нагрузок равен
. В направлении одной из них разброс нагрузок равен  . Следовательно, область разброса нагрузок – отрезок прямой, а инвариант
. Следовательно, область разброса нагрузок – отрезок прямой, а инвариант 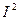 достигает наибольшего значения. Доказательство последнего утверждения проводится при помощи неравенства Коши-Буняковского (35). Во всех остальных случаях, когда
достигает наибольшего значения. Доказательство последнего утверждения проводится при помощи неравенства Коши-Буняковского (35). Во всех остальных случаях, когда 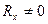 ,
, 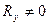 и
и 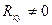 , область разброса нагрузок группы приёмников – эллипс, вытянутость которого с возрастанием
, область разброса нагрузок группы приёмников – эллипс, вытянутость которого с возрастанием 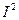 увеличивается. Для описания формы области разброса нагрузок удобнее использовать безразмерный показатель, построенный из инвариантов
увеличивается. Для описания формы области разброса нагрузок удобнее использовать безразмерный показатель, построенный из инвариантов 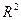 и
и 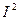 и выраженный формулой
и выраженный формулой
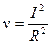 . (43)
. (43)
Этот показатель изменяется от 0 до 1. Он равен нулю, когда 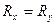 и
и 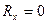 , а область разброса – круг. Если же область разброса нагрузок – отрезок прямой, то
, а область разброса – круг. Если же область разброса нагрузок – отрезок прямой, то  ,
, 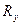 и
и 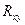 в общем случае связаны соотношением
в общем случае связаны соотношением
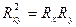 , (44)
, (44)
следующим из неравенства (35) Коши-Буняковского. Из этого соотношения
 . (45)
. (45)
Во всех остальных случаях 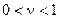 область разброса нагрузок – эллипс, вытянутость которого увеличивается с возрастанием
область разброса нагрузок – эллипс, вытянутость которого увеличивается с возрастанием  . Главные оси эллипса выражают через показатель разброса и инвариант
. Главные оси эллипса выражают через показатель разброса и инвариант 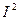 при помощи соотношений
при помощи соотношений
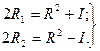 (46)
(46)
Чтобы получить эти соотношения, надо в формулы (31), выражающие преобразование компонент тензора при повороте системы координат на угол 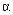 , вместо
, вместо 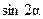 и
и 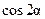 подставить их выражения из (39), определяющие направление главных осей разброса нагрузок. Тогда получим, что главные оси разброса нагрузок равны
подставить их выражения из (39), определяющие направление главных осей разброса нагрузок. Тогда получим, что главные оси разброса нагрузок равны
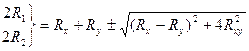 , (47)
, (47)
откуда следуют соотношения (46).
Отношение главных осей разброса нагрузок выражают через показатель формы области разброса нагрузок. Поделив первое равенство из (28.46) на второе, получим
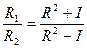 (48)
(48)
и далее, поделив числитель и знаменатель правой части этого равенства на 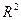 , получим
, получим
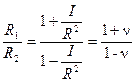 , (49)
, (49)
например, если  , то отношение главных осей разброса нагрузок равно:
, то отношение главных осей разброса нагрузок равно:
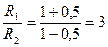 .
.
Дата добавления: 2015-12-17; просмотров: 806;
