Разложение показателя разброса нагрузок на составляющие
Пусть имеется множество G приёмников 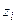 ,
, 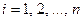 , которое разобьём на s произвольных групп,
, которое разобьём на s произвольных групп, 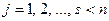 . Запишем показатель разброса нагрузок всего множества G приемников относительно точки, имеющей координаты (
. Запишем показатель разброса нагрузок всего множества G приемников относительно точки, имеющей координаты ( 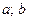 ):
):
 (12)
(12)
где 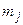 – количество приёмников электроэнергии в j-й группе.
– количество приёмников электроэнергии в j-й группе.
Разложение этого показателя производим при помощи следующего преобразования:
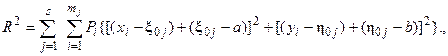 (13)
(13)
Раскроем в (13) все квадраты разностей (  ), произведём группировку слагаемых относительно них и, приняв во внимание, что (
), произведём группировку слагаемых относительно них и, приняв во внимание, что ( 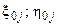 ) – координаты ЦЭН j-й группы приёмников
) – координаты ЦЭН j-й группы приёмников
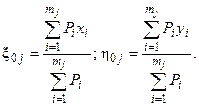 (14)
(14)
получим
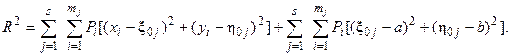 (15)
(15)
Условие (14) определяет, что суммы
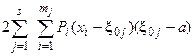
и

равны нулю. В правой части равенства (15) в первом слагаемом под знаком суммы 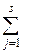 выражение
выражение
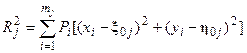 (16)
(16)
является показателем разброса нагрузок приёмников в группе с номером j относительно своего ЦЭН. А второе слагаемое под знаком суммы
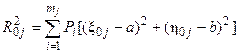
является показателем разброса нагрузки 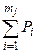 , j-й группы относительно исходной точки (
, j-й группы относительно исходной точки ( 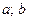 ).
).
Таким образом, показатель разброса нагрузок всего множества G приёмников, вычисленный относительно заданной точки, разлагается на сумму показателей разброса нагрузок групп приёмников относительно их ЦЭН и сумму показателей разброса нагрузок самих групп  относительно исходной точки с координатами (
относительно исходной точки с координатами ( 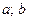 )
)
 (17)
(17)
Для фиксированной точки ( 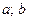 ) значение разброса
) значение разброса 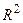 постоянно и не зависит ни от числа групп приёмников, ни от способов распределения приёмников электроэнергии по ним. Разбиение приёмников электроэнергии, минимизирующее суммарный разброс
постоянно и не зависит ни от числа групп приёмников, ни от способов распределения приёмников электроэнергии по ним. Разбиение приёмников электроэнергии, минимизирующее суммарный разброс 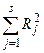 , равносильно максимизации величины
, равносильно максимизации величины 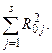 С увеличением числа групп первое слагаемое (17) уменьшается, а второе возрастает, и когда число групп будет равно числу приёмников электроэнергии, т.е.
С увеличением числа групп первое слагаемое (17) уменьшается, а второе возрастает, и когда число групп будет равно числу приёмников электроэнергии, т.е. 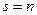 , то
, то 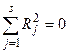 , a
, a  .
.
Допустим, что приёмники электроэнергии должны быть связаны по группам распределительной сетью, передающей электроэнергию напряжением  от источников питания, расположенных в ЦЭН групп, а источники питания должны быть связаны питающей сетью, передающей электроэнергию напряжением
от источников питания, расположенных в ЦЭН групп, а источники питания должны быть связаны питающей сетью, передающей электроэнергию напряжением  (
( 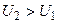 ) от источника питания, расположенного в точке (
) от источника питания, расположенного в точке ( 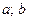 ). Тогда распределение приёмников на группы по заданному числу s источников питания, минимизирующее суммарный показатель разброса нагрузок
). Тогда распределение приёмников на группы по заданному числу s источников питания, минимизирующее суммарный показатель разброса нагрузок 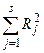 , приводит к уменьшению затрат на распределительную сеть и увеличению затрат на питающую сеть. Но снижение затрат
, приводит к уменьшению затрат на распределительную сеть и увеличению затрат на питающую сеть. Но снижение затрат 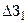 на распределительную сеть больше увеличения затрат
на распределительную сеть больше увеличения затрат 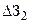 (
( 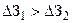 ) на питающую сеть. Следовательно, (17) и его слагаемые могут быть использованы в качестве целевых функций для постановки и решения следующих задач:
) на питающую сеть. Следовательно, (17) и его слагаемые могут быть использованы в качестве целевых функций для постановки и решения следующих задач:
1) об оптимальном распределении приёмников электроэнергии промышленного объекта по заданному числу источников питания с определением мест расположения последних в центрах нагрузок групп;
2) об оптимальном числе источников питания для заданного множества приёмников электроэнергии промышленного объекта.
Дата добавления: 2015-12-17; просмотров: 821;
