Элементы зонной теории твердого тела
1. Удельная электропроводность полупроводников
Свойство твердого тела и в данном случае полупроводника проводить электрический ток количественно характеризуется удельной электропроводностью 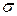 , определяемой в общем виде формулой
, определяемой в общем виде формулой
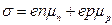 , (1)
, (1)
где 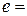 1,6·10-19 Кл – заряд электрона; n и р – концентрации электронов и дырок соответственно;
1,6·10-19 Кл – заряд электрона; n и р – концентрации электронов и дырок соответственно; 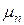 и
и 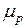 – подвижность электронов и дырок.
– подвижность электронов и дырок.
Из формулы (1) следует, что для определения удельной электропроводности полупроводника необходимо найти концентрацию носителей заряда и их подвижность.
Количественная оценка концентрации носителей заряда может быть произведена на основе их распределения по энергетическим уровням.
Концентрация носителей заряда в собственном полупроводнике.
Определим концентрацию электронов 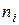 в зоне проводимости полупроводника, помня, чтоконцентрация дырок
в зоне проводимости полупроводника, помня, чтоконцентрация дырок 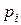 =
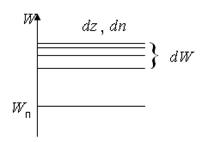
= 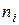 . Для этого выделим в зоне проводимости интервал значения энергии
. Для этого выделим в зоне проводимости интервал значения энергии 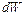 , в котором содержится
, в котором содержится 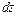 энергетических уровней, и на которых располагаются
энергетических уровней, и на которых располагаются 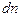 электронов (рис.1 ).
электронов (рис.1 ).
|
 Введем функцию
Введем функцию 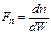 - плотность распределения электронов по энергетическим уровням, знание которой позволит найти концентрацию электронов как
- плотность распределения электронов по энергетическим уровням, знание которой позволит найти концентрацию электронов как
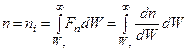 (2)
(2)
Для нахождения функции 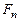 представим ее в виде произведения двух вероятностных функций, известных из курса физики, умножив и разделив ее на величину
представим ее в виде произведения двух вероятностных функций, известных из курса физики, умножив и разделив ее на величину 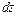 :
:

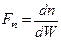 =
= 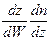 (3)
(3)
Первая функция в произведении отображает плотность распределения энергетических уровней в зоне проводимости и может быть выражена в виде
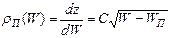 , (4)
, (4)
где С = 8 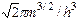 ; m – масса электрона;
; m – масса электрона; 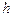 - постоянная Планка. Графическое изображение функции показано на рис.2.
- постоянная Планка. Графическое изображение функции показано на рис.2.
Вторая функция определяет вероятность занятия электроном уровня энергии 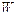 при условии, что плотность энергетических уровней в зоне проводимости постоянна, и определяется статистическим законом Ферми-Дирака
при условии, что плотность энергетических уровней в зоне проводимости постоянна, и определяется статистическим законом Ферми-Дирака
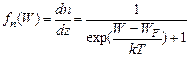 , (5)
, (5)
где 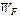 - энергия (уровень) Ферми – энергетический уровень, вероятность заполнения которого
- энергия (уровень) Ферми – энергетический уровень, вероятность заполнения которого 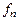 = 0,5;
= 0,5; 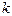 - постоянная Больцмана. График, построенный в соответствии с выражением (5), показан на рис. 2 .
- постоянная Больцмана. График, построенный в соответствии с выражением (5), показан на рис. 2 .
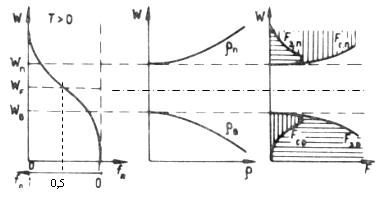
Рис.2
Подставив соотношения ( 4) и ( 5) в формулу (2) с учетом выражения (3), получим
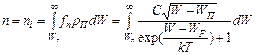 (6)
(6)
Интеграл в выражении (6) в аналитическом виде не берется. Однако при выполнении условия 
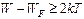 экспоненциальный член в знаменателе подынтегрального выражения оказывается значительно больше единицы и распределение Ферми-Дирака переходит в распределение Максвелла-Больцмана:
экспоненциальный член в знаменателе подынтегрального выражения оказывается значительно больше единицы и распределение Ферми-Дирака переходит в распределение Максвелла-Больцмана:
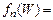
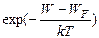 (7 )
(7 )
Указанное условие, называемое иногда критерием вырождения, выполняется для большинства полупроводников, поэтому, в частности, для собственных полупроводников допустимо приближение (7), означающее, что электроны (дырки) в полупроводнике образуют “электронный” (“дырочный”) газ, подчиняющийся статистике Максвелла-Больцмана, который иногда называют невырожденным газом.
В соответствии с принятым условием из соотношения (6) получаем
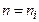 =
= 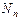
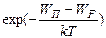 , (8)
, (8)
где 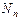 =2
=2 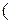 2
2 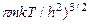

Аналогично определяется концентрация дырок в валентной зоне собственного полупроводника:
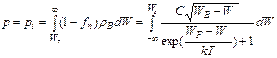 =
=
= 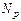
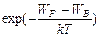 , (9)
, (9)
где 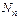 =
= 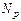 .
.
Результаты графического перемножения ординат соответствующих функций подынтегральных выражений (6) и (9) показаны на рис. 2.
На рис.2 горизонтальной штриховкой обозначена область занятых уровней, а вертикальной – область свободных уровней. Заштрихованная горизонтально под кривой 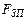 ( или
( или 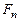 ) в зоне проводимости площадь с занятыми уровнями определяет концентрацию электронов в полупроводнике, а заштрихованная горизонтально под кривой
) в зоне проводимости площадь с занятыми уровнями определяет концентрацию электронов в полупроводнике, а заштрихованная горизонтально под кривой 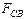 ( или
( или 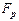 ) в валентной зоне площадь со свободными уровнями - концентрацию дырок. Площади участков под отмеченными кривыми с максимумом равны, так как концентрации дырок и электронов в собственном полупроводнике одинаковы.
) в валентной зоне площадь со свободными уровнями - концентрацию дырок. Площади участков под отмеченными кривыми с максимумом равны, так как концентрации дырок и электронов в собственном полупроводнике одинаковы.
В заключение, учитывая, что 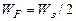 , найдем произведение концентрации электронов на концентрацию дырок, определяемых формулами (6) и (9):
, найдем произведение концентрации электронов на концентрацию дырок, определяемых формулами (6) и (9):
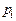
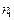 =
= 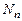
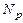
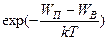 =
= 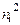 (10)
(10)
Из выражения (10) следует, что зависимость концентрации равновесных носителе заряда в собственном полупроводнике от температуры и ширины запрещенной зоны 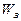 =
= 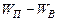 носит экспоненциальный характер.
носит экспоненциальный характер.
Концентрация носителей заряда в примесном полупроводнике. Примесный полупроводник, как отмечалось выше, характерен тем, что в нем концентрация носителей заряда одного знака преобладает над концентрацией носителей заряда другого знака.
Концентрация носителей заряда в примесном полупроводнике определяется общими выражениями (6) и (9) с учетом расположения уровня Ферми в электронном полупроводнике выше середины запрещенной зоны (выше уровня 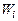 ), а в дырочном полупроводнике – ниже середины запрещенной зоны.
), а в дырочном полупроводнике – ниже середины запрещенной зоны.
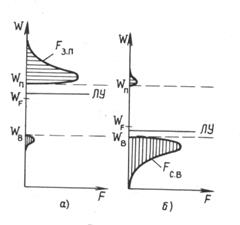
Выполняя операции, аналогичные проводившимся для собственного полупроводника, определим графическим путем концентрации носителей заряда в зонах полупроводника. Результат решения этой задачи для электронного и дырочного полупроводников представлен соответственно на рис.3,а,б. Основное отличие от собственного полупроводника состоит в неравенстве площадей участков под кривыми 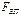 в зоне проводимости и
в зоне проводимости и 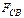 в валентной зоне для электронного полупроводника и площади участков под кривыми
в валентной зоне для электронного полупроводника и площади участков под кривыми 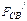 в валентной зоне и
в валентной зоне и 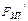 в зоне проводимости дырочного полупроводника, обусловленные неравенством концентрации основных и неосновных носителей заряда.
в зоне проводимости дырочного полупроводника, обусловленные неравенством концентрации основных и неосновных носителей заряда.
|
|
Для примесного, как и для собственного полупроводника, справедливо соотношение 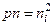 , которое позволяет определить концентрацию неосновных носителей заряда при известной концетрации примесей. Полагая, что все примеси ионизированы, т.е.
, которое позволяет определить концентрацию неосновных носителей заряда при известной концетрации примесей. Полагая, что все примеси ионизированы, т.е. 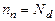 в электронном полупроводнике и
в электронном полупроводнике и 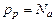 в дырочном полупроводнике, находим
в дырочном полупроводнике, находим
для электронного полупроводника — 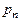 =
= 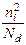 ,
,
для дырочного полупроводника — 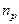 =
= 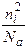 .
.
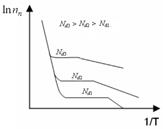
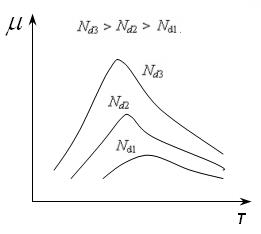
Влияние температуры и уровня концентрации примеси на концентрацию носителей заряда в примесном полупроводнике на примере электронного полупроводника иллюстрирует зависимость 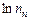 от температуры Т, показанная на рис. 4.
от температуры Т, показанная на рис. 4.
| |
|

| |

| |
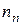 обусловлен ионизацией атомов примеси (доноров); на участке 2 атомы примеси, начиная с комнатной температуры, практически полностью ионизированы и поэтому кон-
обусловлен ионизацией атомов примеси (доноров); на участке 2 атомы примеси, начиная с комнатной температуры, практически полностью ионизированы и поэтому кон-
центрация 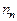 не изменяется; в дальнейшем на участке 3 с повышением температуры происходит резкое увеличение концентрации носителей заряда пар электрон - дырка, вызванное ионизацией атомов собственного полупроводника. При увеличении концентрации примеси энергия активации уменьшается и кривые смещаются кверху.
не изменяется; в дальнейшем на участке 3 с повышением температуры происходит резкое увеличение концентрации носителей заряда пар электрон - дырка, вызванное ионизацией атомов собственного полупроводника. При увеличении концентрации примеси энергия активации уменьшается и кривые смещаются кверху.
2. Движение носителей заряда в полупроводнике
В полупроводнике в состоянии равновесия носители заряда под действием тепловой энергии совершают хаотическое тепловое движение. При этом они не являются свободными в полном смысле этого слова, так как перемещаясь внутри кристаллической решетки и подвергаясь периодическому воздействию электрического поля атомов или дефектов решетки, оказываются связанными при своем движении с каким-либо атомом или дефектом. В этом случае скорость носителей заряда периодически изменяется, остается постоянной лишь их средняя скорость. В идеальном кристаллическом полупроводнике носители заряда движутся равномерно и прямолинейно с постоянной тепловой скоростью vТ. Вследствие хаотического движения носителей заряда их преимущественно направленная вдоль какой-либо пространственной координаты средняя скорость движения
vср.max = 0.
Движение носителей заряда в полупроводнике приобретает направленность (vср.max  0) в двух случаях: при возникновении в кристалле электрического поля (дрейф носителей заряда) и изменении их концентрации (диффузия носителей заряда).
0) в двух случаях: при возникновении в кристалле электрического поля (дрейф носителей заряда) и изменении их концентрации (диффузия носителей заряда).
Дрейф носителей заряда, подвижность. Средняя скорость направленного движения носителей заряда в кристалле (дрейфовая скорость) пропорциональна напряженности электрического поля Е и равна
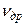 =
= 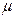 Е,
Е,
где 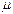 - подвижность носителей заряда. Коэффициент
- подвижность носителей заряда. Коэффициент 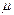 численно равен дрейфовой скорости при единичной напряженности электрического поля и количественно характеризует способность носителей заряда перемещаться (дрейфовать) в электрическом поле. Он может быть определен как
численно равен дрейфовой скорости при единичной напряженности электрического поля и количественно характеризует способность носителей заряда перемещаться (дрейфовать) в электрическом поле. Он может быть определен как
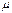 =
= 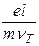 ,
,
где е и m– заряд и эффективная масса носителя заряда;  - длина свободного пробега носителя заряда при тепловой скорости vТ.
- длина свободного пробега носителя заряда при тепловой скорости vТ.
Подвижность носителей заряда наряду с их концентрацией, как отмечалось выше, определяет удельную электропроводность полупроводника и также, в свою очередь, зависит от температуры и концентрации примеси.
|
|
|

 Зависимость величины
Зависимость величины 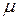 от температуры (рис.5) обусловлена основными механизмами столкновения носителей заряда (механизмами рассеяния): с решеткой (атомами основного вещества и дефектами решетки), подвергающейся тепловым колебаниям, и с ионизированными атомами примесей. Действие обоих механизмов неодинаково при различных температурах и приводит к появлению максимума подвижности при некоторой температуре, который смещается в сторону более низких температур с ростом концентрации примесей.
от температуры (рис.5) обусловлена основными механизмами столкновения носителей заряда (механизмами рассеяния): с решеткой (атомами основного вещества и дефектами решетки), подвергающейся тепловым колебаниям, и с ионизированными атомами примесей. Действие обоих механизмов неодинаково при различных температурах и приводит к появлению максимума подвижности при некоторой температуре, который смещается в сторону более низких температур с ростом концентрации примесей.
Зависимость удельной электропроводности от температуры. В качестве примера найдем зависимость от температуры удельной электропроводности электронного полупроводника. Для этого в соответствии с формулой (1) запишем
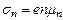 (11)
(11)
Прологарифмировав обе части этого выражения, получаем
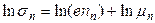 (12)
(12)
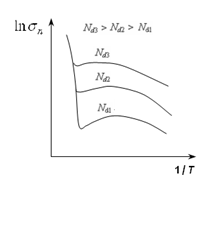
Таким образом, зависимость 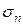 от температуры можно получить, суммируя логарифмы ранее полученных функций. Графическое решение этой задачи приведено на рис.6
от температуры можно получить, суммируя логарифмы ранее полученных функций. Графическое решение этой задачи приведено на рис.6
|
|
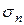 от температуры повторяет зависимость концентрации носителей заряда от Т. В области постоянной концентрации носителей заряда (области эксплуатации) изменение
от температуры повторяет зависимость концентрации носителей заряда от Т. В области постоянной концентрации носителей заряда (области эксплуатации) изменение 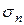 обусловлено подвижностью носителей заряда. При высоких концентрациях примесей (см. рис.4) полупроводник становится вырожденным и в некотором диапазоне температур его электропроводность приобретает такой же характер, как и у металла.
обусловлено подвижностью носителей заряда. При высоких концентрациях примесей (см. рис.4) полупроводник становится вырожденным и в некотором диапазоне температур его электропроводность приобретает такой же характер, как и у металла.
Диффузия носителей заряда. Вероятность столкновения друг с другом носителей заряда в полупроводнике возрастает с увеличением их концентрации. Поэтому при наличии перепада (градиента) концентрации вдоль некоторой пространственной координаты носителя заряда, совершая хаотическое тепловое движение, будут отклоняться в сторону меньших столкновений – смещаться (диффундировать) в сторону уменьшения их концентрации. С увеличением градиента концентрации интенсивность их движения в сторону меньшей концентрации возрастает.
Изменение концентрации носителей заряда в полупроводнике может быть получено, например, путем воздействия на него электромагнитного излучения определенной частоты. В результате в нем может быть создано неравновесное состояние, при котором произведение 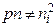 . Генерация в кристалле новых пар носителей заряда в месте воздействия электромагнитного излучения приводит к образованию неравновесных носителей заряда, называемой избыточной —
. Генерация в кристалле новых пар носителей заряда в месте воздействия электромагнитного излучения приводит к образованию неравновесных носителей заряда, называемой избыточной — 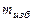 . Из-за наличия градиента концентрации избыточные носители заряда будут диффундировать в сторону от места генерации. При этом в каждом единичном объеме кристалла часть носителей заряда исчезает, рекомбинируя с носителями заряда другого знака, и величина
. Из-за наличия градиента концентрации избыточные носители заряда будут диффундировать в сторону от места генерации. При этом в каждом единичном объеме кристалла часть носителей заряда исчезает, рекомбинируя с носителями заряда другого знака, и величина 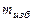 постепенно уменьшается. Концентрация избыточных носителей заряда, например, вдоль некоторой оси
постепенно уменьшается. Концентрация избыточных носителей заряда, например, вдоль некоторой оси 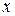 (рис. 7 ) в кристалле уменьшается по экспоненциальному закону
(рис. 7 ) в кристалле уменьшается по экспоненциальному закону
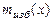 =
= 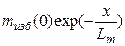 (13)
(13)
где 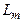 - диффузионная длина носителей заряда данного типа (р или n) в данном полупроводнике, определяемая расстоянием, на котором концентрация избыточных носителей заряда уменьшается в
- диффузионная длина носителей заряда данного типа (р или n) в данном полупроводнике, определяемая расстоянием, на котором концентрация избыточных носителей заряда уменьшается в 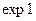 раз. Диффузионная длина носителей заряда в полупроводниках составляет 0,01 – 0,1 см.
раз. Диффузионная длина носителей заряда в полупроводниках составляет 0,01 – 0,1 см.
Скорость, с которой избыточные носители заряда диффундируют вдоль оси 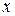 , равна
, равна
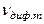 =
= 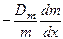 , (14)
, (14)
где 
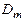 - коэффициент диффузии носителей заряда данного типа – число носителей заряда, диффундирующих за одну секунду через единичную площадку при единичном градиенте концентрации. Коэффициент
- коэффициент диффузии носителей заряда данного типа – число носителей заряда, диффундирующих за одну секунду через единичную площадку при единичном градиенте концентрации. Коэффициент 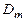 для полупроводников составляет 10 – 103 см2 /с.
для полупроводников составляет 10 – 103 см2 /с.
Связь между введенными выше подвижностью носителей заряда и коэффициентом диффузии определяется соотношением Эйнштейна
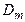 =
= 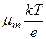 =
= 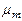
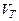 , (15)
, (15)
где 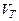 - тепловой потенциал.
- тепловой потенциал.
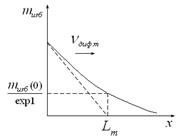
Рис.7
|
|
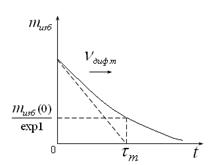
Рис.8
Процесс перехода полупроводника к равновесному состоянию в простейшем случае описывается экспоненциальной функцией
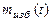 =
= 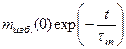 , (16)
, (16)
где 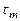 - среднее время жизни носителей заряда – время, в течение которого концентрация избыточных носителей заряда уменьшается в
- среднее время жизни носителей заряда – время, в течение которого концентрация избыточных носителей заряда уменьшается в 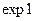 раз. Среднее время жизни в полупроводниках составляет порядок
раз. Среднее время жизни в полупроводниках составляет порядок
10-9 – 10-3 с.
Величины 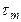 и
и 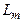 связаны соотношением
связаны соотношением
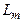 =
= 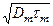 (17)
(17)
3. Токи в полупроводниках
Выше отмечалось, что движение носителей заряда в полупроводниках определяется двумя причинами: наличием в полупроводнике электрического поля и градиента концентрации. Первая причина, вызывая дрейф носителей заряда, а вторая – их диффузию, приводят к протеканию в полупроводнике соответственно дрейфового тока (тока проводимости) и диффузионного тока .
Плотность тока в полупроводниках имеет четыре составляющие, обусловленные двумя видами носителей заряда – электронами и дырками.
Ток дрейфа. Плотность дрейфового тока – электронной и дырочной составляющих может быть записана в виде:
- электронного
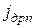 =
= 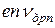 =
= 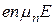 =
= 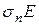 (18)
(18)
- дырочного
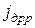 =
= 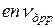 =
= 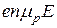 =
= 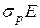 (19 )
(19 )
Ток диффузии. Плотность диффузионного тока:
- электронного
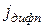 =
= 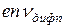 =
= 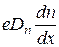 (20)
(20)
- дырочного
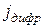 =
= 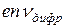 =
= 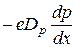 (21)
(21)
Плотность полного тока в полупроводнике соответственно будет:
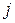 =
= 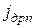 +
+ 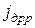 +
+ 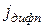 +
+ 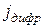 (22)
(22)
| <== предыдущая лекция | | | следующая лекция ==> |
| Историческая справка. Пути развития электроники | | | Физические процессы при контакте твердых тел |
Дата добавления: 2015-12-16; просмотров: 1078;
