Параллельный колебательный контур

Резонанс токов

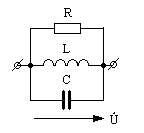
Явление резонанса токов проще всего изучать в электрической цепи с параллельно соединенными r ,L, C, так как при этом можно непосредственно воспользоваться результатами предыдущего параграфа.

Действительно, комплексная проводимость параллельного колебательного контура.

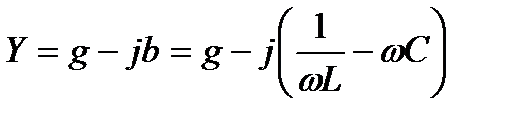
по своей структуре аналогична выражению комплексного сопротивления последовательного колебательного контура, а резонансная частота, как и в предыдущем случае, равна :

.

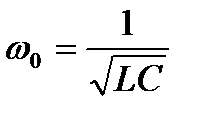Добротность рассматриваемого контура на основании (7.3) равна:

,

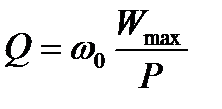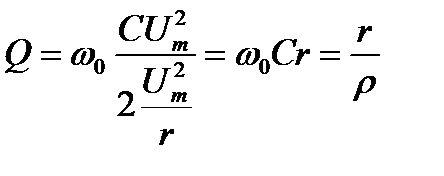, , (7.23)

т.е. обратная по величине добротности последовательного контура r ,L, C.

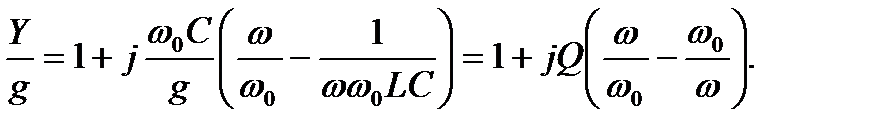
рис. 7.10 Параллельный колебательный контур

По аналогии с предыдущим выражение (7.23) приводится к виду

.

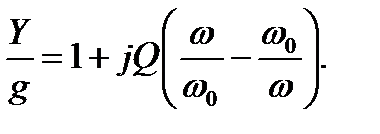
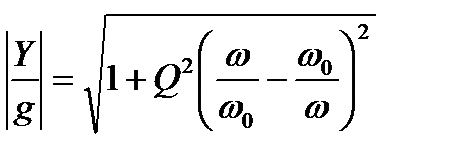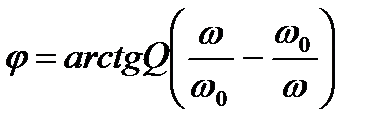(7.24)

Ток, идущий от источника в цепь, отнесенный к току в неразветвленной цепи при резонансе, равен:

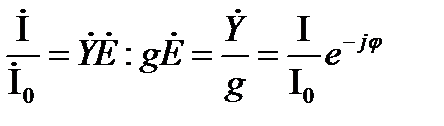
. (7.25)

Сравнивая полученный результат с (7-11), убеждаемся в том, что выражение

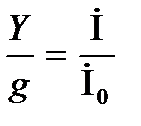для рассматриваемого параллельного колебательного контура имеет тот же вид, что и выражение Z/r для последовательного контура

,

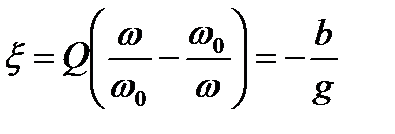получим нормированную характеристику Y/g= 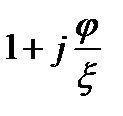. Поэтому кривые рис. 7.6 и 7.8 применимы и в данном случае: кривые рис. 7.6, а и 7.8 ,а выражают зависимость от ω/ω₀ и от ξ отношения Y/g=I/I₀, а кривые рис. 7.6,б и 7.8 , в выражают зависимость φ от ω/ω₀ и от…

При частотах ниже резонансной проводимость индуктивной ветви больше проводимости емкостной ветви, и поэтому выходная проводимость параллельного контура имеет активно-индуктивный характер. При частотах выше резонансной емкостная проводимость больше индуктивной и выходная проводимость контура имеет активно-емкостный характер.

При резонансе токов полная проводимость параллельного колебательного контура рис.7-10 минимальна, т.е. входное сопротивление достигает максимума.При этом ток, идущий от источника, минимален и равен I₀=gE, а токи в индуктивном и емкостном элементах равны по величине и противоположны по знаку:

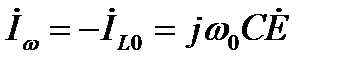
Полученное выражение показывает, что добротность рассматриваемого параллельного колебательного контура определяется как кратность токов в L и C по от отношению к суммарному току I₀ .

При Q>I эти токи превышают по величине I₀ . Поэтому резонанс в параллельном колебательном контуре и называется резонансом токов.

При определении полосы пропускания параллельного колебательного контура исходят из предположения, что контур питается источником тока (не зависящим от частоты), причем границы полосы пропускания соответствуют уменьшению напряжения на контуре по сравнению с напряжением при резонансе в 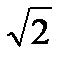раз.

В случае идеального источника тока (с бесконечно большим внутренним сопротивлением ) полоса пропускания параллельного контура вычисляется как d=I/Q.

Если источник тока имеет внутреннее сопротивление r, то чем меньше будет сопротивление r,тем ниже будет эквивалентная добротность

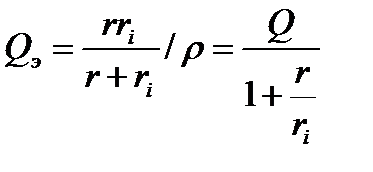и тем шире полоса пропускания контура d_э=1/Q_э. Поэтому в отличие от последовательного колебательного контура с точки зрения сокращения полосы пропускания параллельного колебательного контура выгоден источник тока с большим внутренним сопротивлением.

При резонансе токов, как и при резонансе напряжений, происходит непрерывный обмен энергии между индуктивными и емкостными элементами. Ели бы параллельный колебательный контур состоял только из L и C, соединенных параллельно, то его входное сопротивление при резонансе было бы бесконечно велико и ток от источника в контур не поступал бы. Энергия , первоначально сообщенная контуру , не расходовалась бы, а периодически перераспределялась бы между магнитным и электрическим полями, источник можно было бы отключить, и колебания продолжались бы неограниченное время.

Такой колебательный контур, как и на рисунке 7-10, является идеализированным, так как не учитывает потерь энергии в параллельных ветвях L и C контура.