Последовательный колебательный контур
Резонансная цепь с последовательным соединением 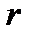 ,
, 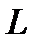 ,
, 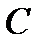 (рис. 7-1) является простейшей цепью для изучения явления резонанса напряжений и подробно рассматривается ниже.
(рис. 7-1) является простейшей цепью для изучения явления резонанса напряжений и подробно рассматривается ниже.
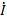
|
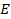 r
r 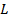
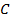
Рис. 7.1 Резонансная цепь с последовательным соединением 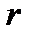 ,
, 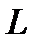 ,
, 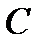
Комплексноe сопротивление такой цепи зависит от частоты:
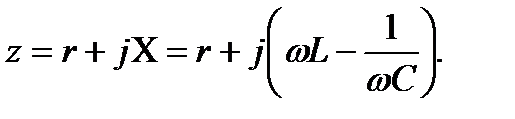 (7.1)
(7.1)
Резонанс напряжений наступает при частоте 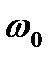 , когда
, когда
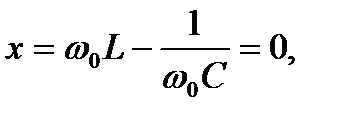
отсюда 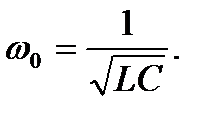 (7.2)
(7.2)
Мгновенные значения энергии выражаются формулами:
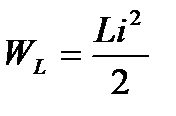 ;
; 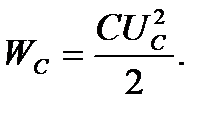
Если принять 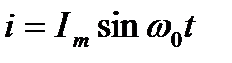 , то
, то 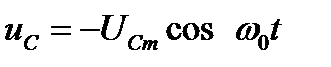 . Поэтому
. Поэтому
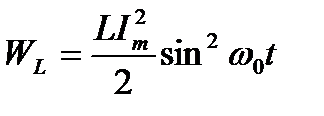 и
и 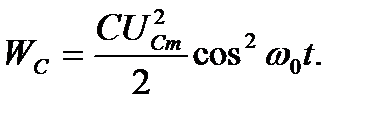
Максимальные значения этих энергий равны друг другу, так как
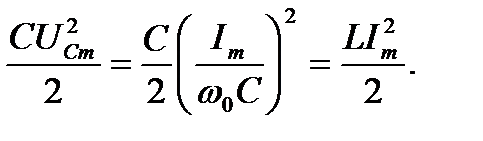
Мгновенные значения энергий 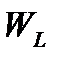 и
и 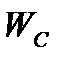 колеблются с удвоенной частотой около среднего значения
колеблются с удвоенной частотой около среднего значения 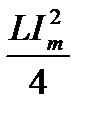 , причем происходит непрерывное перераспределение энергии магнитного и электрического полей, суммарное значение которой постоянно:
, причем происходит непрерывное перераспределение энергии магнитного и электрического полей, суммарное значение которой постоянно:
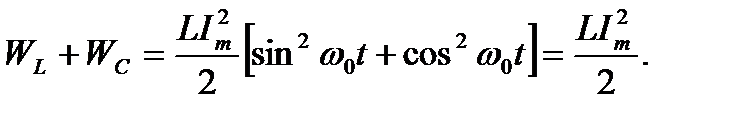
В рассматриваемом случае (резонанс напряжений, рис. 7.1) в цепи не происходит обмена энергии между источником и реактивными элементами цепи, а вся электрическая энергия, поступающая от источника, расходуется в сопротивлении r, преобразуясь в тепловую энергию.
Иначе говоря, энергия, первоначально запасенная в контуре при подключении его к источнику, «колеблется» в режиме резонанса между 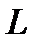 и
и 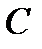 без участия в этом процессе источника. Именно поэтому контур называется колебательным.
без участия в этом процессе источника. Именно поэтому контур называется колебательным.
Если бы колебательный контур не содержал сопротивления r, то при резонансе энергия не поступала бы в контур от источника. При наличии в последовательном контуре сопротивления r вся электрическая энергия, которая при резонансе поступает в контур от источника, расходуется в сопротивлении. За один период она равна
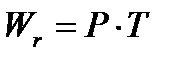 ,
,
где 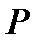 – средняя мощность на зажимах контура при резонансе,
– средняя мощность на зажимах контура при резонансе, 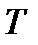 – период.
– период.
Эта энергия обычно во много раз меньше той, которая запасена в колебательном контуре.
Мы уже встречались с понятием добротности индуктивной катушки 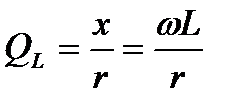 и конденсатора
и конденсатора 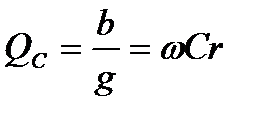
Умножив и разделив выражение для 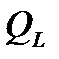 на
на 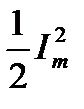 получим:
получим:
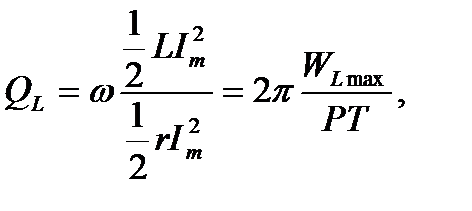
здесь  – средняя мощность, расходуемая за период в последовательном сопротивлении
– средняя мощность, расходуемая за период в последовательном сопротивлении 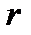 при амплитуде тока
при амплитуде тока 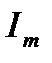 .
.
Аналогично рассуждая, т. е. умножив и разделив выражение на 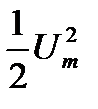 , получим:
, получим: 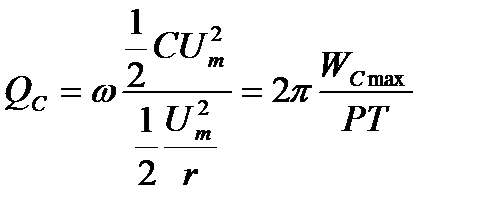 ,
,
где 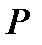 – средняя мощность, расходуемая в параллельном сопротивлении r при амплитуде напряжения на емкости
– средняя мощность, расходуемая в параллельном сопротивлении r при амплитуде напряжения на емкости 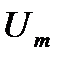 .
.
Следовательно, добротность определяется в зависимости от отношения максимума энергии реактивного элемента к энергии, поглощаемой сопротивлением за период. В обоих случаях добротность равна отношению реактивной мощности (взятой с положительным знаком) к средней мощности.
В случае колебательной цепи также пользуются понятием добротности контура
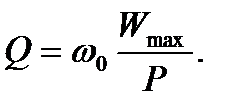 (7.3)
(7.3)
Следует обратить внимание на то, что все величины, входящие в (7.3), соответствуют условию резонанса.
Для последовательного колебательного контура (рис. 7.1) на основании
(7.3) получаем:
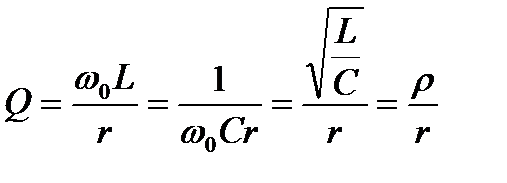 , (7.4)
, (7.4)
где 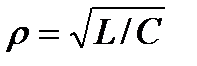 называется характеристическим (или волновым) сопротивлением колебательного контура.
называется характеристическим (или волновым) сопротивлением колебательного контура.
Характеристическое сопротивление составляет в среднем несколько сотен Ом, а сопротивление r несколько Ом; поэтому добротность колебательных контуров, применяемых в радиотехнике, достигает ≈100÷300.
Величина, обратная добротности контура, называется затуханием контура и обозначается:
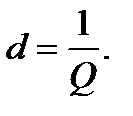 (7.5)
(7.5)
Это наименование связано с тем, что при отключении колебательного контура от источника, когда контур замыкается накоротко, колебательный процесс затухает тем интенсивнее, чем больше величина 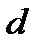 .
.

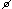
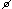
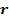
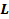
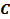
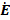
а)
| rBH |
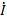
|
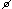
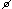
| L |
| r |
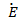
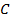
б)
Рис. 7-3. Нагруженный колебательный контур
В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например к емкости, подключается нагрузка в виде сопротивления 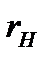 (рис. 7.3, а). Вследствие этого возрастают потери в цепи и уменьшается добротность.
(рис. 7.3, а). Вследствие этого возрастают потери в цепи и уменьшается добротность.
Для определения добротности нагруженного контура параллельное соединение 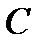 и
и 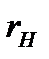 можно заменить эквивалентным при резонансной частоте последовательным соединением емкости и «вносимого» сопротивления
можно заменить эквивалентным при резонансной частоте последовательным соединением емкости и «вносимого» сопротивления 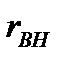 (рис. 7.3, б). Переписывая соотношение в виде:
(рис. 7.3, б). Переписывая соотношение в виде:
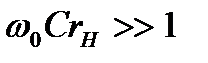 ,
, 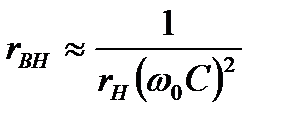
и учитывая, что 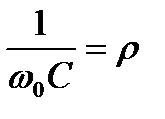 , получаем:
, получаем: 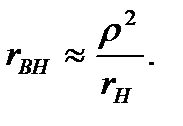
Как отмечалось при высоких частотах, емкости эквивалентных схем (рис. 7-3, а и б) могут быть приравнены друг к другу.
Таким образом, в схеме (рис. 7-3, б) содержатся те же реактивные элементы, а сопротивление равно 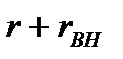 .
.
Добротность нагруженного контура равна:
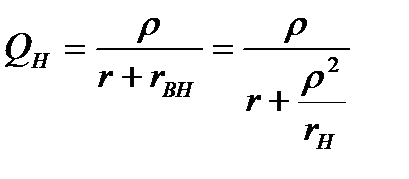 , (7.6)
, (7.6)
а затухание увеличивается на величину «вносимого» затухания
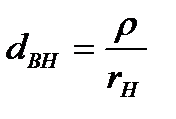
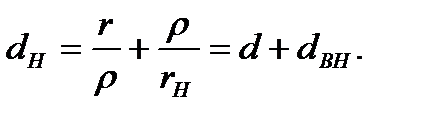 (7.7)
(7.7)
Если вносимое сопротивление 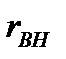 значительно превышает сопротивление
значительно превышает сопротивление 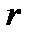 , то
, то
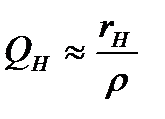 ;
; 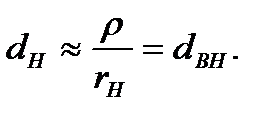 (7.8)
(7.8)
При резонансе входное сопротивление последовательного контура минимально, а ток в контуре достигает максимальной величины. Поэтому в условиях, близких к резонансу, напряжения на индуктивности и емкости могут быть значительно больше приложенного к цепи напряжения.
На рис. 7-4 показана векторная диаграмма тока и напряжения при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения:
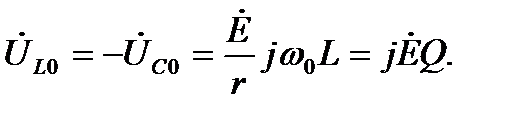 (7.9)
(7.9)
При 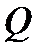 >1 эти напряжения превышают по величине напряжение
>1 эти напряжения превышают по величине напряжение 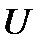 =
= 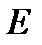 , приложенное к колебательному контуру. Поэтому резонанс в последовательном колебательном контуре называется резонансом напряжений.
, приложенное к колебательному контуру. Поэтому резонанс в последовательном колебательном контуре называется резонансом напряжений.
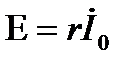 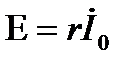
|
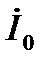
|
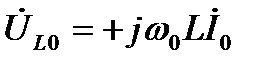
|
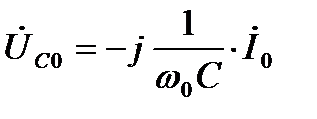
|
Рис. 7.4
Из (7-9) следует, что
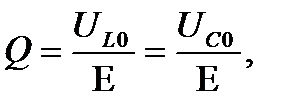 (7.10)
(7.10)
т. е. добротность рассматриваемой цепи определяется отношением напряжения на 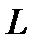 или
или 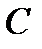 при резонансе к величине приложенного к контуру напряжения.
при резонансе к величине приложенного к контуру напряжения.
Из (7.2) следует, что резонанс напряжений может быть достигнут изменением параметров 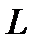 и
и 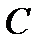 (при фиксированной частоте
(при фиксированной частоте 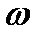 источника напряжения) или частоты источника
источника напряжения) или частоты источника 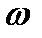 (при фиксированных параметрах
(при фиксированных параметрах 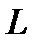 и
и 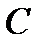 ).
).
а) б)
Рис. 7.5
Зависимости тока в контуре и напряжений на индуктивности и емкости от 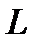 или
или 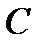 при заданной частоте называются настроечными кривыми.
при заданной частоте называются настроечными кривыми.
На рис. 7.5 показаны кривые тока в зависимости от 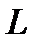 и
и 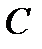 . Они построены по формуле:
. Они построены по формуле:
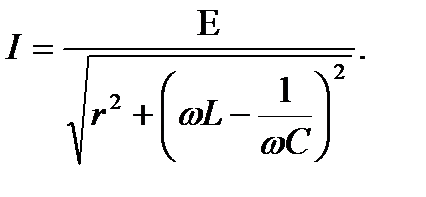
При 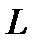 =0 ток равен:
=0 ток равен:
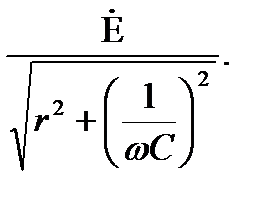
При 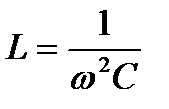 ток достигает максимального значения
ток достигает максимального значения 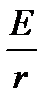 , и по мере увеличения
, и по мере увеличения 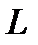 ток спадает, стремясь к нулю при
ток спадает, стремясь к нулю при 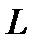
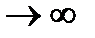 .
.
При C=0 ток отсутствует. При 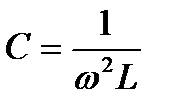 ток достигает максимума, а затем с увеличением
ток достигает максимума, а затем с увеличением 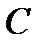 стремится в пределе к
стремится в пределе к
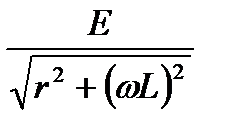 .
.
Значения 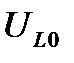 и
и 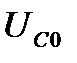 , получаемые на основании (7.9), не являются экстремальными: максимум напряжения
, получаемые на основании (7.9), не являются экстремальными: максимум напряжения 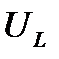 наступает при частоте выше резонансной, а максимум
наступает при частоте выше резонансной, а максимум 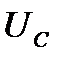 – при частоте ниже резонансной. Более подробно этот вопрос рассмотрен в конце § 7.3.
– при частоте ниже резонансной. Более подробно этот вопрос рассмотрен в конце § 7.3.
Дата добавления: 2015-12-16; просмотров: 1955;
