Сети Петри. Построение моделей на основе сетей Петри.

Широкое использование параллельных и распределенных вычислительных систем требует применения математических моделей, описывающих параллельные процессы. Аппаратом описания сложных систем взаимодействующих процессов являются формальные системы типа сетей Петри, которые позволяют моделировать динамические свойства системы. Формализм сетей Петри общего вида основан на понятии комплекта. В этой теории это понятие является обобщением понятия множества.

Комплект – набор элементов, но, в отличии от множества, всякий элемент может входить в него более одного раза. Иначе говоря, отношение включения, связывающее элементы и множества заменяются на функцию числа экземпляров элементов в комплекте. 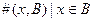– число 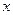в комплекте 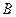. Множество – частный случай комплекта. Многие понятия теории множеств распространяются и на комплекты.

Мощность комплекта – общее число экземпляров элементов в комплекте.

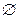– пустой комплект.

Комплект 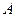включен в комплект 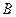(является подкомплектом): .

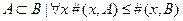С помощью функции числа экземпляров ( 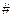) легко определить операции над комплектами:

1. Объединение комплектов

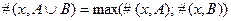
2. Пересечение комплектов

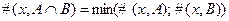
3. Разность комплектов

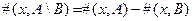
Если 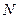– множество, то 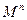– множество всех таких комплектов, построенных из элементов множества 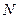, что .

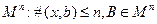Сеть Петри – это четверка 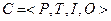, где 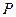– конечное число позиций; 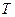– конечное число переходов; 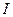– входная функция, отображающая переходы в комплекты позиций; 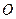– выходная функция, отображающая переходы в комплекты позиций.

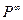– множество всех комплектов, построенное из элементов 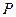без ограничения на число экземпляров элементов в комплекте.

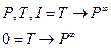
Графически сеть Петри изображают в виде мультиграфа с вершинами двух видов. Кружки соответствуют позициям, планки – переходам. Функци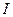и и представляются дугами.

Пример: мультиграф сети Петри.

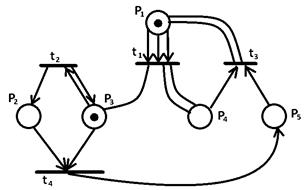
Позиции, дуги из которых ведут в переход , называются входными для . Аналогично позиции, в которые ведут дуги из перехода 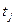, называются выходными для 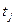. Множество входных позиций обозначают 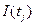. Множество выходных позиций .

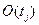В сети Петри, изображенной на рисунке, входные позиции для 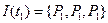, выходные позиции для .

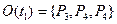Функци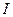и и 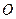удобно обобщить и на отображении из позиции в комплекты переходов 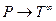, что позволяет обозначить множество входных и выходных переходов позиций .

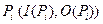В сети Петри, изображенной на рисунке, для позиции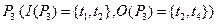

Введенные понятия относятся к статическим структурам сети Петри. Динамические свойства сети Петри определяются с помощью понятия маркировки. Маркировка 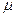сети Петри, определяющаяся как 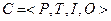– функция, отображающая множество позиций 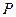в множество неотрицательных целых чисел 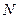. . 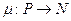Маркировка изображается с помощью помещаемых внутрь позиций фишек (точек).

Маркировка сети в приведенном примере определяется следующим образом:

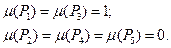
Удобно представить маркировку как 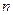-вектор 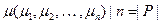, каждый элемент которого 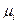есть 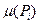, а также как комплект 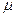, в который входят позиции сет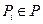и и .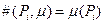

Сеть Петри с определенной на ней маркировкой называется маркированной сетью Петри.

Маркировка сети может изменяться в результате запуска переходов. Переход 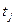маркированной сети Петри с маркировкой 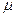называется разрешенным, если 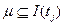, т.е. в каждой входной позиции 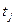находится не меньше точек, чем из этой позиции исходит дуг в 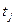. Всякий разрешенный переход может запуститься. В результате запуска перехода 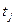маркировка сети 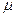заменяется на новую 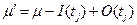, т.е из всякой входной позиции 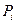перехода 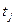удаляется столько точек, сколько дуг ведет из 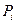в 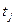, а в каждую выходную позицию 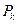помещается столько точек, сколько дуг ведет из 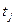в 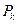.Последовательность запусков переходов называется выполнением сети Петри.

Рассмотрим выполнение сети Петри для примера. В качестве маркировки разрешен только переход 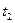. При его запуске точка удаляется из 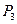, а затем в позици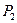и и 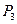добавится по точке, т.е. в результате запуска в новой маркировке 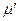появится точка еще и в 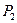. Теперь становятся разрешенными переходы 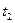и 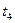. Поскольку запуститься может любой разрешенный переход, предположим, что запустился 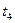. После его запуска из позици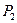й и 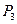точки удалятся, а в позиции 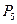появится одна точка. В полученной маркировке 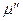не разрешен ни один переход. На этом выполнение сети Петри заканчивается.

Рассмотрим маркировку сети Петри, представленную четверкой 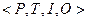. Маркировка 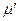называется непосредственно достижимой из 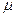, если найдется такой переход 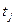, разрешенный в 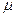, что при его запуске получается маркировка 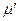. В этом случае пара 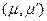принадлежит отношению непосредственной достижимости. Транзитивное замыкание этого отношения называется отношением достижимости. Маркировки 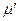, такие что 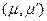принадлежат отношению достижимости, называются достижимыми из 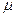. Множество достижимых из 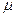маркировок сети Петри называется множеством достижимости и обозначается .

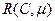Интерпретация сетей Петри основана на понятиях условия и события. Состояния системы описываются совокупностью условий. Функционирование системы состоит в осуществлении последовательности определенных действий, т.е. событий.

Для возникновения события необходимо выполнение некоторых условий, называемых предусловиями. Возникновение события может привести к нарушению предусловия и выполнению постусловий. Условия моделируются позициями, события – переходами. Предусловия событий представляются входными позициями соответствующего перехода, постусловия – выходными позициями. Возникновение события моделируется запуском перехода. Выполнение условий представляет наличие точек в соответствующих позициях, невыполнение – их отсутствие.

Рассмотрим пример моделирования простой вычислительной системы с последовательной обработкой заданий, которые поступают во входную очередь. Когда процессор свободен и во входной очереди имеется задание, оно обрабатывается процессором, затем выводится.

Эту систему можно промоделировать сетью Петри, представленную следующим мультиграфом:

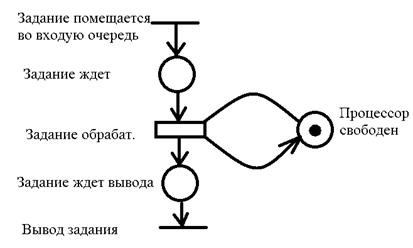
Установим, какие особенности систем учитывают сети Петри. Это, прежде всего, асинхронность. В сетях Петри отсутствует понятие времени. Время возникновения события не указывается, но, тем не менее, структура сети Петри устанавливает частотный порядок возникновения событий. Далее, поскольку возникновение событий представляется запуском переходов, предполагается, что события происходят мгновенно. Если же моделируемое событие имеет отличную от нуля длительность (например, «задание обрабатывается») и это существенно, то оно представляется в виде двух мгновенных событий типа «начало события» - «конец события» и условия «событие происходит». Считается, что события происходят не одновременно.

Другим важным свойством сетей Петри является их способность представлять параллелизм и конфликтные ситуации. Параллелизм представляется двумя разрешимыми переходами, множества которые не пересекаются.