Цепь, содержащая резистор и индуктивную катушку

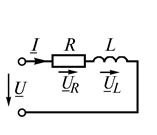
Реальная катушка в цепи переменного тока представляет сочетание актив­ной и индуктивной составляющих сопротивления. Схема замещения индуктивной катушки представлена на рис 2.9 а. Пусть по катушке протекает ток .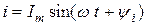

а)	б)	в)

Рис. 2.9

В соответствии со вторым законом Кирхгофа для мгновенных значений

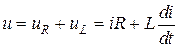, (2.18)

где 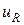– напряжение на активном сопротивлении; 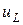– напряжение на индуктив­ном сопротивлении.

Для действующих значений уравнение (2.18) можно записать

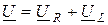. (2.19)

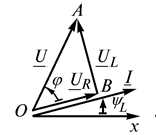
Построим векторную диаграмму в соответствии с (2.19) в такой последовательности. Изобразим вектор тока 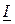(основной вектор) на координатной плоскости 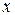– 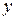(рис. 2.9 б). Затем строим вектор напряжения на ак­тивной составляющей сопротивления 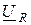. Он совпадает по фазе с током. Вектор напряжения 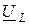опережает вектор тока на 90°. Сумма двух векторов дает вектор напряжения источника, который опережает вектор тока на угол 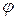. Из векторной диаграммы следует

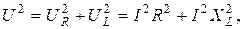
отсюда

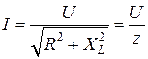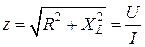, . (2.20)

где z – полное сопротивление цепи R, L.

Треугольник ОАВ (рис. 2.9 б) назовем треугольником напряжений. Состав­ляющая напряжения, находящаяся в фазе с током, называется актив­ной составляющей напряжения

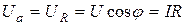. (2.21)

Составляющая напряжения, перпендикулярная вектору тока, называется реак­тивной составляющей напряжения

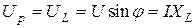. (2.22)

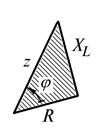
Если стороны треугольника напряжений (рис. 2.9 б) разделить на действующее значение тока, то получим треугольник сопротивлений (рис. 2.9 в). Из треуголь­ника сопротивлений получают соотношения для угла сдвига фаз, а также связь между параметрами цепи

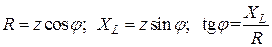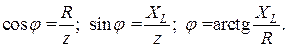; (2.23)

Цепь имеет индуктивный характер, если 0< 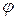< 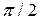. Крайние значения
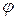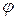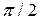= 0 и = соответствуют чисто активной и чисто индуктивному характеру нагрузки.