Последовательное соединение резистора, катушки и конденсатора
При протекании синусоидального тока 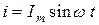 по цепи, состоящей из последовательно соединенных элементов
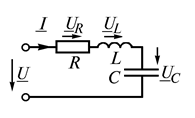
по цепи, состоящей из последовательно соединенных элементов 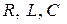 (рис. 2.11 а), на ее зажимах создается синусоидальное напряжение, равное алгебраической сумме синусоидальных напряжений на отдельных элементах (второй закон Кирхгофа):
(рис. 2.11 а), на ее зажимах создается синусоидальное напряжение, равное алгебраической сумме синусоидальных напряжений на отдельных элементах (второй закон Кирхгофа):
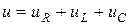 .
.
Для действующих значений это уравнение имеет вид
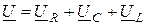 .
.
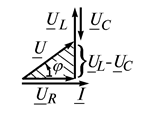
Построим векторную диаграмму с учетом известных фазовых соотношений (рис. 2.11 б). Вектор напряжения на резисторе совпадает по фазе с вектором тока, на конденсаторе он отстает от вектора тока на 90°, а на катушке опережает вектор тока на 90°. Сумма этих векторов напряжения на элементах цепи, даст вектор напряжения источника.
| 
| 
|
| а) | б) | в) |
Рис. 2.11
Из векторной диаграммы определяем входное напряжение
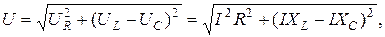
откуда ток и полное сопротивление
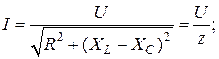
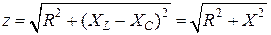 , (2.26)
, (2.26)
где 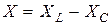 – разность индуктивного и емкостного сопротивлений, называемая реактивным сопротивлением.
– разность индуктивного и емкостного сопротивлений, называемая реактивным сопротивлением.
Сдвиг фаз определим из треугольника напряжений или сопротивлений:
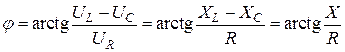 .
.
Если 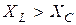 , т.е.
, т.е. 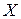 > 0, то цепь имеет индуктивный характер. В этом случае
> 0, то цепь имеет индуктивный характер. В этом случае 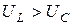 (рис. 2.11 б), а сдвиг фаз
(рис. 2.11 б), а сдвиг фаз 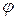 > 0. Если
> 0. Если 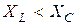 , т.е.
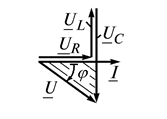
, т.е. 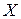 < 0, то цепь имеет емкостный характер и сдвиг фаз
< 0, то цепь имеет емкостный характер и сдвиг фаз 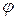 < 0 (рис. 2.11 в). Таким образом, реактивное сопротивление
< 0 (рис. 2.11 в). Таким образом, реактивное сопротивление 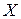 может быть положительным (
может быть положительным ( 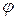 > 0) и отрицательным (
> 0) и отрицательным ( 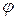 < 0).
< 0).
Особый случай цепи, когда 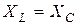 , т.е. реактивное сопротивление
, т.е. реактивное сопротивление 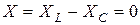 . В этом случае цепь имеет чисто активный характер, а сдвиг фаз
. В этом случае цепь имеет чисто активный характер, а сдвиг фаз 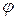 = 0. Такой режим называется резонансом напряжений.
= 0. Такой режим называется резонансом напряжений.
Условием резонанса напряжений является
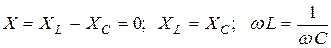 .
.
Эти условия показывает, что резонанс напряжений в цепи можно получить изменением частоты напряжения источника, или индуктивности катушки или емкости конденсатора.
Угловая частота, при которой в цепи наступает резонанс напряжений, называется резонансной угловой частотой
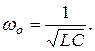
Полное сопротивление цепи минимальное и равно активному
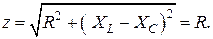
Ток в цепи, очевидно, будет максимальным
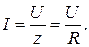
Напряжение на резисторе равно напряжению источника: 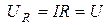 .
.
Резонанс напряжений, как правило, нежелателен в электроэнергетике, но широко применяется в радиотехнических устройствах, автоматике, телемеханике, связи, измерительной технике и др..
III. Расчёт электрического состояния цепи с последовательным соединением элементов L, R, C.
Рассмотрим цепь из трех последовательных токоприемников (рис. 2.12 а): первые два имеют активно-индуктивный характер, третий является последовательным соединением резистора и конденсатора. Проведем анализ цепи по векторной диаграмме. Произвольно строим вектор тока, который является базовым для всех векторов диаграммы. В соответствии со вторым законом Кирхгофа
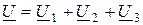 ,
,
где 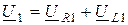 ;
; 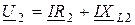 ;
; 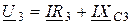 .
.
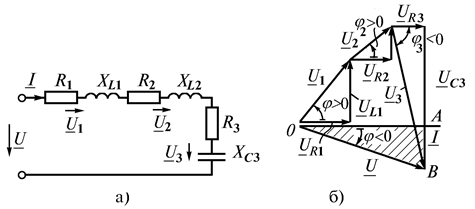
Рис. 2.12
Строим составляющие векторы, модули которых определяются по закону Ома. Суммарный вектор строим по правилу многоугольника. Векторы напряжений на активных сопротивлениях цепи совпадают по фазе с вектором тока, векторы 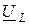 опережают вектор тока на 90°, а вектор
опережают вектор тока на 90°, а вектор 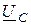 отстает от него на угол 90° (рис. 2.12 б). Действующее значение напряжения источника (модуль вектора
отстает от него на угол 90° (рис. 2.12 б). Действующее значение напряжения источника (модуль вектора 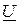 ) по диаграмме находится из треугольника напряжений ОАВ
) по диаграмме находится из треугольника напряжений ОАВ
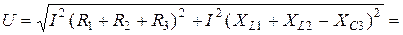
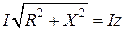 . (2.27)
. (2.27)
В формуле (2.27) 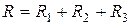 – активное сопротивление цепи, равное арифметической сумме сопротивлений последовательно включенных резисторов. В общем случае для
– активное сопротивление цепи, равное арифметической сумме сопротивлений последовательно включенных резисторов. В общем случае для 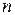 последовательных приемников
последовательных приемников
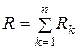 .
.
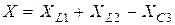 является реактивным сопротивлением цепи, равным алгебраической сумме реактивных сопротивлений последовательно включенных элементов. В общем случае
является реактивным сопротивлением цепи, равным алгебраической сумме реактивных сопротивлений последовательно включенных элементов. В общем случае
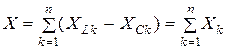 .
.
В приведенной схеме сумма векторов индуктивных напряжений меньше вектора напряжения на конденсаторе, поэтому 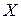 < 0. В таком случае говорят, что реактивное сопротивление (или цепь в целом) носит емкостный характер.
< 0. В таком случае говорят, что реактивное сопротивление (или цепь в целом) носит емкостный характер.
Для проверки проводим расчёт активной и реактивной мощности и полной мощности P, Q и S:
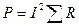
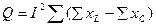 U=UI
U=UI
IV. Расчёт цепи с параллельным соединением R, L, C элементов
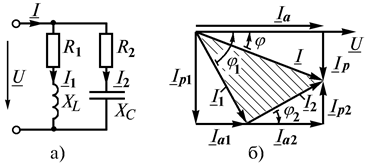 Рис. 2.13
Рис. 2.13
|
Рассмотрим цепь из двух параллельных ветвей (рис. 2.13 а). Допустим, что известны напряжение источника и параметры схемы. Нужно определить ток 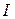 , потребляемый от источника, и угол сдвига
, потребляемый от источника, и угол сдвига 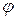 на входе цепи. Для получения расчетных соотношений построим векторную диаграмму токов. Предварительно рассчитаем токи в параллельных ветвях и углы их сдвига относительно приложенного напряжения. У первой ветви характер нагрузки индуктивный, ток отстает от
на входе цепи. Для получения расчетных соотношений построим векторную диаграмму токов. Предварительно рассчитаем токи в параллельных ветвях и углы их сдвига относительно приложенного напряжения. У первой ветви характер нагрузки индуктивный, ток отстает от 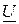 на угол
на угол 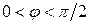
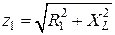 ;
; 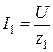 ;
; 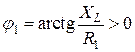 .
.
У второй ветви характер нагрузки емкостный, вектор 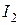 опережает
опережает 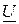 на угол
на угол 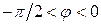
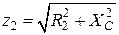 ;
; 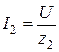 ;
; 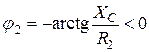 .
.
В качестве основного вектора принимаем вектор напряжения источника 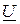 , являющегося общим для двух параллельных ветвей (рис. 2.13 б). Тогда относительно него нетрудно сориентировать векторы токов
, являющегося общим для двух параллельных ветвей (рис. 2.13 б). Тогда относительно него нетрудно сориентировать векторы токов 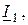
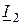 .
.
При выборе направления тока второй ветви угол 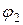 откладываем от вектора
откладываем от вектора 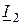 в направлении, параллельном вектору
в направлении, параллельном вектору 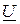 , поскольку начала этих векторов не совмещены. В соответствии с первым законом Кирхгофа (
, поскольку начала этих векторов не совмещены. В соответствии с первым законом Кирхгофа ( 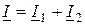 ) определяем входной ток. В дальнейшем все расчетные соотношения получим из векторной диаграммы. Для этого представим каждый вектор проекциями на взаимноперпендикулярные оси. Проекцию вектора тока на вектор напряжения назовем активной составляющей тока
) определяем входной ток. В дальнейшем все расчетные соотношения получим из векторной диаграммы. Для этого представим каждый вектор проекциями на взаимноперпендикулярные оси. Проекцию вектора тока на вектор напряжения назовем активной составляющей тока 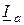 , а перпендикулярную проекцию – реактивной составляющей
, а перпендикулярную проекцию – реактивной составляющей 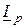 . На диаграмме (рис. 2.13 б) эти составляющие показаны для всех векторов. Составляющие токи
. На диаграмме (рис. 2.13 б) эти составляющие показаны для всех векторов. Составляющие токи 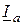 и
и 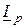 физически не существуют и должны рассматриваться только как расчетные. По диаграмме активная составляющая входного тока определяется как сумма активных составляющих токов в параллельных ветвях
физически не существуют и должны рассматриваться только как расчетные. По диаграмме активная составляющая входного тока определяется как сумма активных составляющих токов в параллельных ветвях
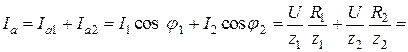
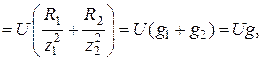 (2.28)
(2.28)
где 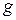 – активная проводимость цепи, равная арифметической сумме активных проводимостей отдельных ветвей
– активная проводимость цепи, равная арифметической сумме активных проводимостей отдельных ветвей
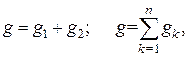
где 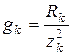 – активная проводимость
– активная проводимость 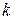 -й ветви.
-й ветви.
Только в частном случае, когда ветвь представляет собой чисто активное сопротивление 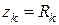 .
.
Реактивная составляющая входного тока определяется как алгебраическая сумма реактивных составляющих токов в параллельных ветвях. Реактивную составляющую ветви с катушкой считают положительной, а с конденсатором – отрицательной. Знаки учитывают при подстановке соответствующих значений
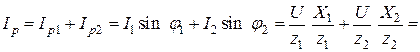
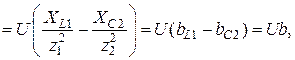 (2.29)
(2.29)
где 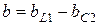 – реактивная составляющая проводимости цепи, равная алгебраической сумме реактивных проводимостей отдельных ветвей.
– реактивная составляющая проводимости цепи, равная алгебраической сумме реактивных проводимостей отдельных ветвей.
В общем случае
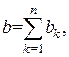
где 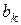 – реактивная проводимость отдельной
– реактивная проводимость отдельной 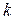 -й ветви,
-й ветви,
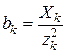 . (2.30)
. (2.30)
Если рассматриваемая ветвь чисто реактивная: 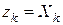 , проводимость
, проводимость 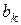 является обратной реактивному сопротивлению. Ток на входе цепи (см. векторную диаграмму на рис. 2.13 б) с учетом (2.28, 2.29)
является обратной реактивному сопротивлению. Ток на входе цепи (см. векторную диаграмму на рис. 2.13 б) с учетом (2.28, 2.29)
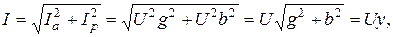 (2.31)
(2.31)
где 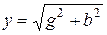 – полная проводимость цепи, равная геометрической сумме активной и реактивной проводимостей.
– полная проводимость цепи, равная геометрической сумме активной и реактивной проводимостей.
Угол сдвига фаз 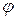 также определяется из векторной диаграммы. На рис. 2.14 а изображена векторная диаграмма входного тока
также определяется из векторной диаграммы. На рис. 2.14 а изображена векторная диаграмма входного тока 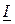 , его составляющих
, его составляющих 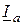 и
и 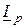 и напряжения источника
и напряжения источника 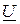 . Треугольник, образованный вектором тока и его проекциями
. Треугольник, образованный вектором тока и его проекциями 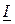 ,
, 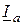 и
и 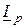 , называется треугольником токов (рис. 2.14 а). Если стороны этого треугольника разделить на напряжение
, называется треугольником токов (рис. 2.14 а). Если стороны этого треугольника разделить на напряжение 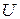 , получится треугольник, подобный треугольнику токов – треугольник проводимостей. Он образован проводимостями
, получится треугольник, подобный треугольнику токов – треугольник проводимостей. Он образован проводимостями 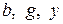 , модули которых равны соответствующим проводимостям, а стороны совпадают с векторами
, модули которых равны соответствующим проводимостям, а стороны совпадают с векторами 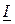 ,
, 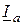 ,
, 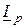 треугольника токов (рис. 2.14 б).
треугольника токов (рис. 2.14 б).

а) б) в)
Рис. 2.14
На рис. 2.14 в показан треугольник проводимостей при 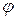 <0. Из него находим соотношения между параметрами и формулы для определения угла сдвига фаз
<0. Из него находим соотношения между параметрами и формулы для определения угла сдвига фаз
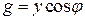 ;
; 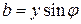 ;
; 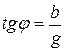 ;
; 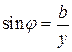 ;
; 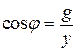 ;
; 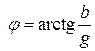 . (2.32)
. (2.32)
Чтобы учесть знак 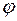 , следует использовать формулы тангенса и синуса.
, следует использовать формулы тангенса и синуса.
В этой цепи, когда общий ток совпадает по фазе с напряжением, а входная реактивная проводимость 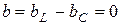 или
или 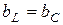 , может возникнуть явление резонанса. При
, может возникнуть явление резонанса. При 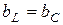 противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название резонанса токов.
противоположные по фазе реактивные составляющие токов равны, поэтому резонанс в такой цепи получил название резонанса токов.
ПримерОпределить действующее значение входного тока по известным токам в параллельных ветвях (риc. 2.15 а) 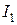 = 3 A;
= 3 A; 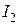 = 1 A;
= 1 A;  = 5 A.
= 5 A.
Решение находим по первому закону Кирхгофа
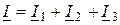 ,
,
в соответствии с которым строим векторную диаграмму.
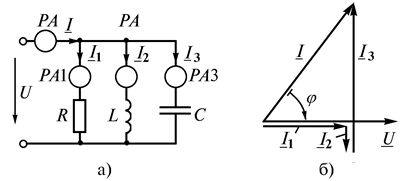
Рис. 2.15
Направления трех слагаемых тока 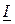 выбраны по отношению к вектору
выбраны по отношению к вектору 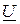 . Из диаграммы (рис. 2.16 б) определяем ток
. Из диаграммы (рис. 2.16 б) определяем ток
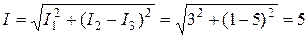 А.
А.
Дата добавления: 2015-12-16; просмотров: 5110;
