ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Электромагнитный процесс в электрической цепи, при котором мгновенные значения напряжений и токов повторяются через равные промежутки времени, называется периодическим. Наименьший промежуток времени, по истечении которого наблюдаются повторения мгновенных значений периодических величин, называется периодом. Если величину, являющуюся периодической функцией времени t,обозначить через F(t), то для любого положительного или отрицательного значения аргумента t справедливо равенство

F(t ± T) = F(t),

где Т - период.

Геометрически это значит, что ординаты двух произвольных точек графика F(t) с абсциссами, отличающимися на Т, одинаковы.

Величина, обратная периоду, т.е. число периодов в единицу времени, называется частотой: f = 1/T.

Частота имеет размерность 1/с, а единицей измерения частоты служит Герц (Гц);частота равна 1 Гц, если период равен 1 с.

Преобладающим видом периодического процесса в электрических цепях является синусоидальный режим, характеризующийся тем, что все напряжения и токи являются синусоидальными функциями одинаковой частоты. Это возможно только при заданных синусоидальных ЭДС и токах источников. Тем самым обеспечивается наиболее выгодный эксплуатационный режим работы электрических установок.

Как известно из курса математического анализа, синусоида является простейшей периодической функцией; всякие другие несинусоидальные периодические функции могут быть разложены в бесконечный ряд синусоид, имеющих кратные частоты. Поэтому для исследования процессов в цепях переменного тока в первую очередь необходимо изучить особенности цепей синусоидального тока. Так как косинусоида может рассматриваться как сдвинутая синусоида, то условимся к синусоидальным функциям причислять и косинусоидальные. Колебания, выражаемые этими функциями, будем называть гармоническими.

На рисунке 2.1 изображены функции

u = U_mcos(ωt + y) (2.1)

и

u = U_msin(ωt + y). (2.2)

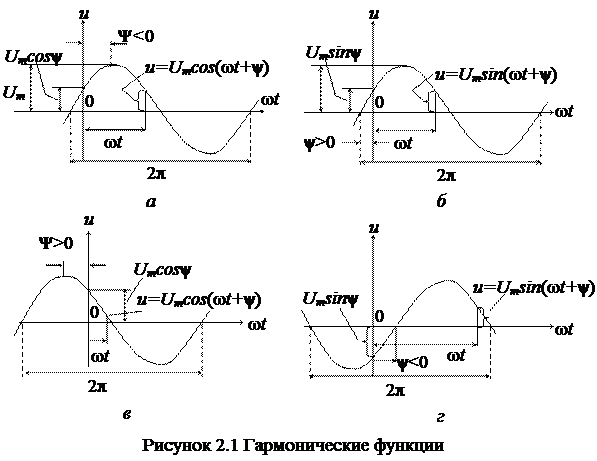
Здесь U_m - максимальное значе­ние функции или амплитуда;

ω - скорость изменения аргумента (угла), называемая угловой частотой; она равна произведению частоты на 2p:

ω = 2pf, рад/сек; (2.3)

y - начальная фаза, определяемая величиной смещения гармонической функции относительно начала координат; при записи (2.1) она измеряется абсциссой положительного максимума, а при записи (2.2) - абсциссой точки перехода отрицательной полуволны в положительную.

Начальная фаза y представляет собой алгебраическую величину. На рисунке 2.1, а и г угол y отрицателен.Нарисунке 2.1, б и в угол yположителен. В дальнейшем будем пользоваться преимущественно записью (2.1).

За аргумент функций (2.1) и (2.2) может быть принято время t или соответственно угол 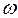t > t. Аргументу t соответствует период Т, а аргументу ωt - период ωТ = 2p.Следует иметь в виду, что аргумент ωt измеряется в радианах, причем в тех же единицах измеряется и начальная фаза.

Если угол y вычисляется в градусах, то аргумент ωt также переводится в градусы. Напомним, что 1 рад = 57,3°. в этом случае период составляет 360°.

Величина ωt + y, определяющая стадию изменения функций (2.1) и (2.2), называется фазовым углом или фазой. С течением времени фаза возрастает, причем после увеличения фазы на 2p цикл изменения синусоидальной величины повторяется.

Рассмотренные в данном параграфе понятия, характеризующие гармонические колебания, являются исходными при изучении электрических процессов в цепях переменного тока.