Некоторые проявления поверхностного натяжения

Опыт Плато

Стремление к уменьшению площади поверхности характерно, не только для тонких пленок, но и для любых объемов жидкости. И если бы поверхностная энергия была единственным видом энергии, определяющим поведение жидкости, то любая масса жидкости всегда должна была бы принимать такую форму, при которой ее поверхность наименьшая. Такой формой, очевидно, является шар, так как именно шар обладает минимальной поверхностью при данном объеме.

Однако кроме внутренних сил взаимодействия между частицами, из-за которых и возникают силы поверхностного натяжения, на жидкость обычно действуют еще и внешние силы. Это, во-первых, сила тяжести и, во-вторых, силы взаимодействия частиц жидкости с частицами твердых стенок сосуда, в котором она содержится. Поэтому действительная форма, которую принимает жидкость, определяется соотношением этих трех сил.

Рассмотрим сначала роль силы тяжести. Это сила объемная, действующая на весь объем жидкости. Так как с изменением массы жидкости ее объем изменяется быстрее, чем ее поверхность, то при достаточно большой массе роль поверхностных сил очень мала по сравнению с силами объемными: поверхностная энергия в этом случае почти не играет роли и форма жидкости определяется главным образом потенциальной энергией, обусловленной силой тяжести. Под действием силы тяжести жидкость стремится разлиться и принять форму тонкого слоя — это соответствует минимальной потенциальной энергии в поле сил тяжести.

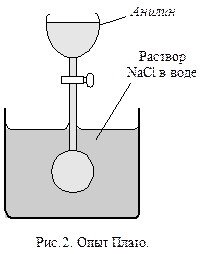Но если тем или иным путем исключить или существенно уменьшить действие силы тяжести, то определяющими окажутся уже силы поверхностного натяжения, даже если они малы. В известном опыте Плато действие силы тяжести исключается тем, что жидкость помещается в другую, не смешивающуюся с нею жидкость с такой же плотностью. Тогда вес жидкости уравновешивается подъемной силой Архимеда и поверхностные силы оказываются единственными определяющими геометрическую форму, которую примет жидкость. В таких случаях жидкость принимает форму шара.

Опыт Плато проводится следующим образом: в сосуд, содержащий раствор поваренной соли в воде, вливают некоторое количество анилина, который не растворяется в растворе NаСl (рис.2). Концентрацию раствора подбирают так, чтобы его плотность была равна плотности анилина. Тогда анилин собирается в шар, плавающий в растворе.

Очень эффектно наблюдали поверхностные силы наши космонавты в полете, когда невесомость обеспечивала шаровую форму жидкости внесосуда.

Капли жидкости

Жидкость принимает сферическую форму не только при искусственной компенсации силы тяжести (как это делается в опыте Плато). Малый объем жидкости сам по себе принимает форму, близкую к шару, так как благодаря малой массе жидкости мала и сила тяжести, действующая на нее. Поверхностная энергия и в этом случае превышает потенциальную энергию силы тяжести и форма жидкости определяется именно ею.

Этим объясняется шарообразная форма небольших капель жидкости. Хорошо известна, например, шаровидная форма капель ртути, у которой коэффициент поверхностного натяжения, как и у многих других расплавленных металлов, довольно велик — около 500 дин/см. Этим же объясняется почти строго шаровидная форма капель жидкости, вытекающих из узкой трубки.

При выходе из трубки размер капли постепенно нарастает, но отрывается она только тогда, когда достигает вполне определенного размера. Это происходит потому, что пока капля недостаточно велика, силы поверхностного натяжения достаточны для того, чтобы противостоять силе тяжести и предотвратить отрыв. Отрыв же произойдет тогда, когда вес капли станет равным силе поверхностного натяжения, удерживающей ее. Отсюда следует, что из наблюдений над отрывом капель можно определить численное значение коэффициента поверхностного натяжения.

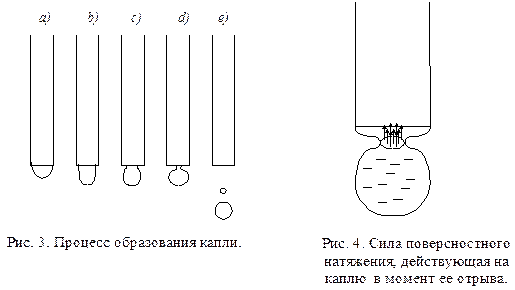
На рис. 3 показан процесс образования капли. Перед отрывом образуется шейка, радиус которой несколько меньше радиуса трубки. Вдоль окружности этой шейки и действует сила поверхностного натяжения (рис.4), которая в момент отрыва должна быть равна силе тяжести.

Если радиус шейки r, а коэффициент поверхностного натяжения жидкости 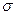, то сила поверхностного натяжения равна, очевидно, 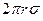. Следовательно, отрыв капли происходит при условии:

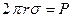. (11)

Измерив вес Р оторвавшейся капли и радиус шейки в момент отрыва, можно вычислить коэффициент поверхностного натяжения жидкости. Для достижения необходимой точности в определении радиуса шейки отрывающуюся каплю проектируют с известным увеличением на экран, где и производится измерение диаметра. Вес Р отрывающейся капли измеряется на аналитических весах. Обычно в целях повышения точности измерения отсчитывают определенное число капель и измеряют их общий вес.

Описанный способ экспериментального определения коэффициента поверхностного натяжения дает хорошие результаты, несмотря на то, что в действительности отрыв капли происходит не совсем так, как описано выше. На самом деле капля не отрывается по линии окружности шейки. В момент, когда размер капли достигает значения, определяемого равенством (11), шейка начинает быстро сужаться, как это показано на рис. 3,d, причем ей сопутствует еще одна маленькая капля, как это показано на рис.3,e.