Коэффициент поверхностного натяжения

Определение коэффициента поверхностного

Натяжения жидкости

Молекулярные явления на границе жидкости

Коэффициент поверхностного натяжения

Поверхность жидкости, соприкасающаяся с другой средой, например с ее собственным паром, с какой-либо другой жидкостью или с твердым телом (частности со стенками сосуда, в котором она содержится), находится в особых условиях по сравнению с остальной массой жидкости.

Возникают эти особые условия потому, что молекулы пограничного слоя жидкости, в отличие от молекул в ее глубине, окружены молекулами той же жидкости не со всех сторон. Часть «соседей» поверхностных молекул – это частицы второй среды, с которой жидкость граничит. Она (эта среда) может отличаться от жидкости как природой, так и плотностью частиц. Имея же разных соседей, молекулы поверхностного слоя и взаимодействуют с ними различным образом. Поэтому силы, действующие на каждую молекулу в этом слое, оказываются неуравновешенными: существует некоторая равнодействующая сила, направленная либо в сторону объема жидкости, либо в сторону объема граничащей с ней среды. Вследствие этого перемещение молекулы из поверхностного слоя в глубь жидкости или в глубь среды, с которой она граничит, сопровождается совершением работы (внутри жидкости молекулы, со всех сторон окруженные точно такими же частицами, находятся в равновесии, и их перемещение не требует затраты работы). Величина и знак этой работы зависят от соотношения между силами взаимодействия молекул поверхностного слоя со «своими» же молекулами и с молекулами второй среды.

В случае, если жидкость граничит со своим собственным паром (насыщенным), т. е. в случае, когда мы имеем дело с одним веществом, сила, испытываемая молекулами поверхностного слоя, направлена внутрь жидкости. Это объясняется тем, что плотность молекул в жидкости много больше, чем в насыщенном паре над жидкостью (вдали от критической температуры), и поэтому сила притяжения, испытываемая молекулой поверхностного слоя со стороны молекул жидкости, больше, чем со стороны молекул пара.

Отсюда следует, что, перемещаясь из поверхностного слоя внутрь жидкости, молекула совершает положительную работу. Наоборот, переход молекул из объема жидкости к поверхности сопровождается отрицательной работой, т. е. требует затраты внешней работы.

Представим себе, что по тем или иным причинам поверхность жидкости увеличивается (растягивается). Это значит, что некоторое количество молекул переходит из объема жидкости в поверхностный слой. Для этого, как мы только что видели, надо затратить внешнюю работу. Другими словами, увеличение поверхности жидкости сопровождается отрицательной работой. Наоборот, при сокращении поверхности совершается положительная работа.

Если при постоянной температуре обратимым путем изменить поверхность жидкости на бесконечно малую величину dS, то необходимая для этого работа

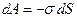(1)

Знак минус указывает на то, что увеличение поверхности (dS > 0) сопровождается отрицательной работой.

Коэффициент 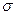является основной величиной, характеризующий свойства поверхности жидкости, и называется коэффициентом поверхностного натяжения ( 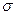>0). Следовательно, коэффициент поверхностного натяжения измеряется работой, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.

Очевидно, в системе СИ 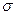имеет размерность Дж/м², а в системе СГС — эрг/см².

Из сказанного ясно, что молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами, находящимися в объеме жидкости, потенциальной энергией. Обозначим ее U_S. Эта энергия, как всегда, измеряется работой, которую могут совершить молекулы поверхности, перемещаясь внутрь жидкости под действием сил притяжения со стороны молекул в объеме жидкости.

Поскольку энергия U_S обязана своим происхождением наличию поверхности жидкости, то она должна быть пропорциональна площади S поверхности жидкости:

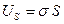(2)

Тогда изменение площади поверхности dS повлечет за собой изменение потенциальной энергии

, (3)

которое сопровождается работой

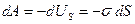. (4)

Если, как было указано, изменение поверхности S осуществляется при постоянной температуре, т. е. изотермически (и обратимо), то, как известно, потребная для этого работа равна изменению свободной энергии F поверхности:

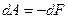. (5)

(Если изменение поверхности жидкости произвести адиабатно, то ее температура изменится. Например, увеличение поверхности приведет к ее охлаждению.) Значит, избыточная потенциальная энергия поверхности жидкости, о которой говорилось выше, является свободной энергией поверхности и, следовательно,

, (6)

т. е. коэффициент поверхностного натяжения жидкости можно определить как свободную энергию единицы площади этой поверхности.

Теперь ясно, в чем заключаются указанные выше особые условия, в которых находится поверхность жидкости. Они заключаются в том, что поверхность жидкости обладает избыточной по сравнению с остальной массой жидкости потенциальной (свободной) энергией.

Посмотрим, к чему это приводит.

Известно, что всякая система при равновесии находится в том из возможных для нее состояний, при котором ее энергия имеет минимальное значение. Применительно к рассматриваемому случаю это означает, что жидкость в равновесии должна иметь минимально возможную поверхность. Это в свою очередь означает, что должны существовать силы, препятствующие увеличению поверхности жидкости, т. е. стремящиеся сократить эту поверхность.

Очевидно, что эти силы должны быть направлены вдоль самой поверхности, по касательной к ней. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются силами поверхностного натяжения.

Нужно, однако, помнить, что первопричиной возникновения сил поверхностного натяжения являются силы, испытываемые молекулами поверхностного слоя, направленные внутрь жидкости, а в некоторых случаях внутрь той среды, с которой она граничит, т. е. перпендикулярно к поверхности.

Для разрыва, или, как говорят, для раздела поверхности необходимо приложить внешние силы, параллельные к поверхности и перпендикулярные к той линии, вдоль которой предполагается разрыв (раздел).

Это особенно ясно видно из опытов с тонкими пленками жидкости. Некоторые жидкости, как, например, мыльная вода, сапонин и др., обладают свойством образовывать тонкие пленки. Если, например, опустить проволочную рамку, одна из сторон которой подвижна (рис. 1), в мыльный раствор, то вся она затянется пленкой жидкости. Силы поверхностного натяжения принуждают пленку сокращаться, и подвижная перекладина АВ вслед за пленкой перемещается вверх. Чтобы сохранить ее в равновесии, к перекладине нужно приложить силу в виде груза (сюда входит и вес самой перекладины).

Таким образом, сила поверхностного натяжения, действующая в пленке, перпендикулярна к линии АВ, которая в данном случае и является линией раздела. Такие же силы действуют, конечно, и на другие стороны рамки. Но здесь они уравновешиваются силами притяжения жидкости к веществу жесткой рамки.

Описанный опыт может быть использован для определения численного значения коэффициента поверхностного натяжения жидкости, образующей пленку. Действительно, поверхностная сила f, с учетом того, что пленка имеет две поверхности (ведь пленка на самом деле представляет собой тонкий слой жидкости), равна при равновесии весу груза Р:

2f =Р и f=Р/2. (7)

Если под действием этой силы перекладина, увлекаемая пленкой, переместилась на расстояние dh из положения АВ, то работа, совершенная силой, равна:

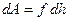. (8)

Работа эта равна уменьшению свободной энергии пленки, которое равно: 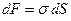. В данном случае dS =l dh, где l — длина рамки. Отсюда

(9)

и

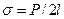. (10)

Из (10) следует, что коэффициент поверхностного натяжения может быть определен как величина, равная силе, действующей по касательной к поверхности жидкости, приходящейся на единицу длины линиираздела.

Определенный таким образом коэффициент поверхностного натяжения измеряется в системе СИ в единицах Н/м, а в системе СГС в дин/см.