Сила вязкого трения

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВНУТРЕННЕГО ТРЕНИЯ

Маловязких жидкостей

Определение вязкости

Примеры проявления вязкости жидкости

Идеальная жидкость, т.е. жидкость без трения, является абстракцией. Всем реальным жидкостям или газам в большей или меньшей степени присуща вязкость, или внутреннее трение. Вязкость проявляется в том, что возникшее в жидкости или газе движение после прекращения действия причин, его вызвавших, постепенно прекращается.

Рассмотрим также следующие примеры, в которых проявляется вязкость жидкости. Так, согласно закону Бернулли для идеальной жидкости, давление в трубе постоянно, если ее поперечное сечение и высота не меняются. Однако, как известно, давление вдоль такой трубы равномерно падает, как показано на рис. 1.

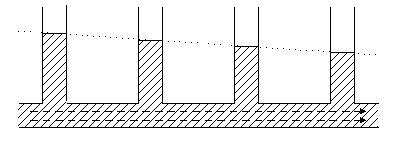
Рис. 1. Падение давления в трубе с движущейся жидкостью.

Это явление объясняется наличием у жидкости внутреннего трения и сопровождается переходом части ее механической энергии во внутреннюю.

При ламинарном течении жидкости по трубе (рис. 2) скорость слоев непрерывно меняется от максимальной (по оси трубы) до нуля (у стенок).

С механической точки зрения любой из слоев тормозит движение соседнего слоя, расположенного ближе к оси трубы (движущегося быстрее), и оказывает ускоряющее действие на слой, расположенный дальше от оси (движущийся медленнее).

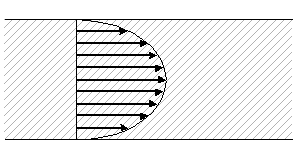
Рис. 2. Распределение скорости в поперечном сечении потока

жидкости в трубе круглого сечения (ламинарное течение).

Сила вязкого трения

Для выяснения закономерностей, которым подчиняются силы внутреннего трения, рассмотрим следующий опыт. В жидкость погружены две параллельные друг другу пластины (рис. 3), линейные размеры которых значительно превосходят расстояние между ними d. Нижняя пластина удерживается на месте, верхняя приводится в движение относительно нижней с некоторой скоростью v₀.

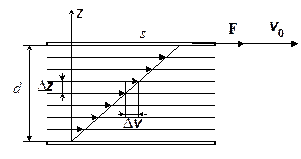
Рис. 3. Послойное движение вязкой жидкости между пластинками,

имеющими различные скорости движения.

Слой жидкости, прилегающей непосредственно к верхней пластинке, благодаря силам молекулярного сцепления прилипает к ней и движется вместе с пластинкой. Слой жидкости, прилипший к нижней пластинке, остается вместе с ней в покое. Промежуточные слои движутся так, что каждый верхний из них обладает скоростью большей, чем под ним лежащий. Т.о. каждый слой скользит относительно соседних слоев. Поэтому со стороны нижнего слоя на верхний действует сила трения, замедляющая движение второго из них, и, обратно, со стороны верхнего на нижний – ускоряющее движение. Силы, возникающие между слоями жидкости, испытывающими относительное перемещение, называют внутренним трением. Свойства жидкости, связанные с наличием сил внутреннего трения, называют вязкостью.

Опыт дает, что для перемещения верхней пластины с постоянной скоростью v₀ необходимо действовать на нее с вполне определенной силой F. Действие внешней силы F уравновешивается равной ей по величине противоположно направленной силой трения.

Сила внутреннего трения между двумя слоями жидкости может быть вычислена по формуле Ньютона:

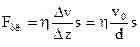, (1)

где h – динамическая вязкость, коэффициент внутреннего трения, s – площадь соприкосновения (в данном случае площадь пластины), Dv/Dz – градиент скорости.

Коэффициент вязкости численно равен силе, действующей на единицу площади слоя, когда на единицу длины, взятой перпендикулярно к слою, скорость меняется на единицу (Dv/Dz=1)

Единица СИ динамической вязкости: [h] = 1Па·с = 1Н·с /м ² = 1кг·м ^–1·с ^–1. В системе СГС [h] = 1г·см ^–1·сек ^–1= 1 П (Пуаз).

Для двух бесконечно близких слоев формула Ньютона примет следующий наиболее общий вид:

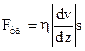. (2)

Эта формула определяет модуль силы трения. Если формула (1) справедлива для случая, когда скорость изменяется по линейному закону от координаты z, то формула (2) остается справедливой и для любого другого закона изменения скорости от слоя к слою.