Структурные типы однослойных углеродных нанотрубок
Однослойная углеродная нанотрубка – нанотрубка со стенкой в один атомарный слой. Диаметр однослойной трубки составляет 0.6-1.8 нм (1.4 нм типичный).
Структурные параметры углеродной нанотрубки определяются структурой базисных плоскостей графита, симметрией кристаллического графенового слоя относительно оси трубки. Сворачивать графеновый слой можно в разных направлениях: вдоль грани шестиугольника – трубки "armchair" (кресельные), перпендикулярно грани – трубки «zigzag" (зигзагные) и во всех промежуточных – "chiral" (хиральные) (рис 7).
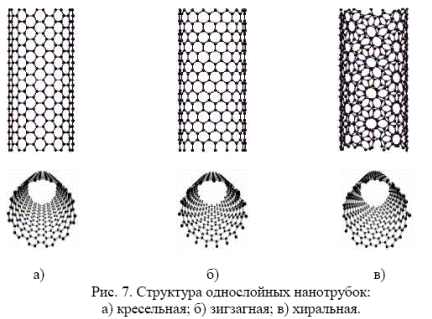
Кресельные и зигзагные нанотрубки имеют высокосимметричную структуру, так кресельные нанотрубки переходят в себя при зеркальном отражении, а зигзагные нанотрубки переходят в себя с точностью до поворота. Хиральные нанотрубки составляют большую часть нанотрубок и не обладают столь высокосимметричной формой. В хиральных нанотрубках гексагоны закручиваются по спирали вокруг оси трубки. При зеркальном отражении хиральная нанотрубка (n,m) переходит в нанотрубку (m,n). Взаимная ориентация гексагональной сетки графита и продольной оси нанотрубки определяет очень важную структурную характеристику нанотрубки – хиральность.
 3.2. Структурные параметры углеродных нанотрубок
3.2. Структурные параметры углеродных нанотрубок
Хиральность (от греч. hiros – рука) – тип зеркальной симметрии, при котором левый и правый варианты фигуры не могут быть совмещены друг с другом (подобно симметрии кистей рук).
Рассмотрим подробно как из графитового листа получаются нанотрубки (рис.8). Вектора а1 и а2 являются базисными векторами элементарной ячейки графитового листа. Вектор С является линейной комбинацией векторов а1 и а2 и соединяет две эквивалентные точки на первичном графитовом листе:
С = na1 + ma2 ,
где n, m - целые числа (n≥m), называемые индексами хиральности.
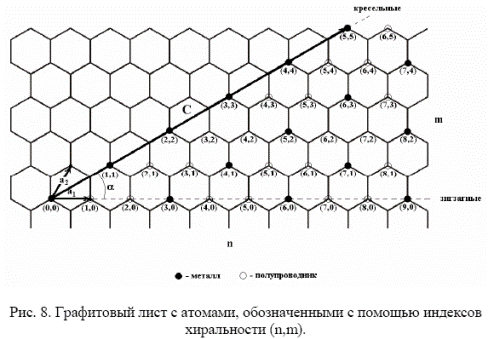
Цилиндр получается при сворачивании графитового листа таким образом, чтобы две конечные точки вектора С совмещались. Вследствие симметрии решетки пчелиных сот множество полученных таким образом цилиндров будут эквивалентными. Однако существует «неприводимый клин», содержащий одну двенадцатую графеновой решетки, с помощью которого определяются элементарные структуры нанотрубок.
Каждая пара чисел (n,m) представляет возможную структуру нанотрубки. Кресельные нанотрубки получаются при n=m , зигзагные – при m=0, все остальные нанотрубки являются хиральными.
Индексы хиральности однослойной нанотрубки определяют ее диаметр D и хиральный угол α-угол между гранью и направлением сворачивания. Так как 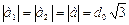 , где d0=0,142 нм – расстояние между атомами углерода в гексагональной сетке графита, получим величину вектора С в нанометрах равную
, где d0=0,142 нм – расстояние между атомами углерода в гексагональной сетке графита, получим величину вектора С в нанометрах равную 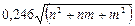 .
.
Диаметр нанотрубки определяется как :
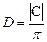
или

Хиральный угол:
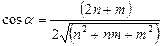
Хиральный угол лежит в пределах 0° ≤ α ≤ 30°. Среди различных возможных направлений сворачивания нанотрубок выделяются направления, для которых совмещение шестиугольника (n,m) с началом координат не требует искажения в его структуре. Этим направлениям соответствуют углы α = 0° и α =30°. Указанные конфигурации отвечают хиральностям (n,0) и (n,n) соответственно.
Если мы полагаем, что нанотрубка является одномерным кристаллом, то можно определить трансляционную элементарную ячейку вдоль оси трубки. Для всех нанотрубок элементарная ячейка трансляции имеет форму цилиндра.
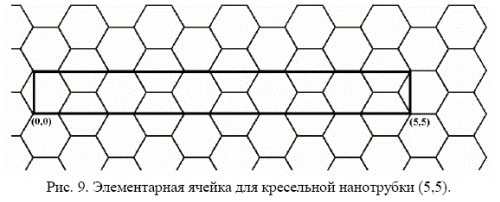
Для кресельной нанотрубки ширина ячейки равна величине элементарного вектора а графитовой сетки (рис. 9).
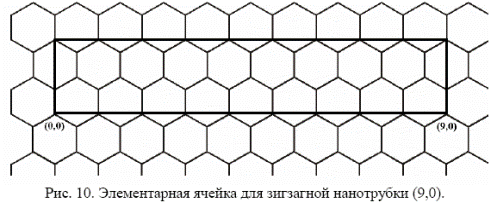
Для зигзагной нанотрубки ширина ячейки составляет 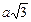 (рис. 10). Кресельные и зигзагные нанотрубки с большим диаметром имеют элементарные ячейки, которые являются просто уширенной версией трубок (5,5) и (9,0) соответственно.
(рис. 10). Кресельные и зигзагные нанотрубки с большим диаметром имеют элементарные ячейки, которые являются просто уширенной версией трубок (5,5) и (9,0) соответственно.
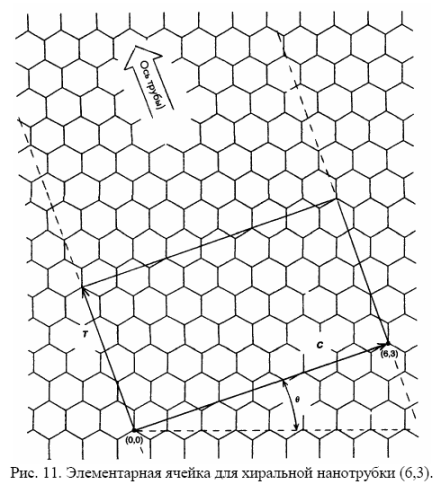
Для хиральных нанотрубок более низкая симметрия приводит к увеличению элементарной ячейки. Рассмотрим метод построения элементарной ячейки для хиральных нанотрубок. Этот метод заключается в построении прямой линии, проходящей через начало неприводимого клина (0,0) нормально к вектору С (рис.11). Длина элементарной ячейки в направлении оси нанотрубки равна величине вектора Т. Выражение для Т может быть получено с помощью длины вектора С и наибольшего делителя для хиральных индексов n и m, который обозначается dH.
Если п - m ≠3rdH, где r – некоторое целое число, то
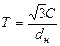
Если n-m=3rdн
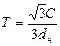
От хиральности зависят свойства нанотрубок (рис. 8). Все кресельные нанотрубок являются металлическими, зигзагные и хиральные нанотрубки в зависимости от индексов хиральности могут обладать как металлическими, так и полупроводниковыми свойствами.
Металлическими свойствами обладает 1/3 зигзагных нанотрубок. В этом случае n должно быть кратно 3. Остальные 2/3 зигзагных нанотрубок являются полупроводниковыми.
1/3 хиральных нанотрубок является металлическими, если выполняется условие n-m=3q, где q - целое число. Остальные 2/3 хиральных нанотрубок, так же как и зигзагные, обладают полупроводниковыми свойствами.
Дата добавления: 2015-12-16; просмотров: 3393;
