Биосенсоры из углеродных нанотрубок

Биосенсоры позволяют быстро и с высокой селективностью проводить автоматизированный анализ сложных по составу объектов, определяя глюкозу, холестерин, мочевину, аминокислоты и другие вещества, содержание которых может изменяться от 0.05 мкг/л до 1мг/л.

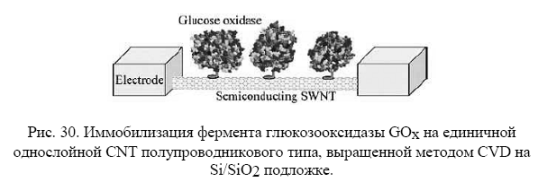
Биосенсор на индивидуальной однослойной углеродной нанотрубке позволяет контролировать рН среды до 0.1 (рис. 30). Иммобилизация GOx существенно уменьшила проводимость однослойной CNT. CNT, покрытые GOx, в отличие от исходных, оказались очень чувствительными к рН среды в диапазоне 4 - 5,5. При рН=5.5 их проводимость значительно повышается, причем изменения проводимости обратимы. Также выяснилось, что покрытые GOx полупроводниковые CNT чувствительны к b-D-глюкозе - при ее добавлении в раствор их проводимость увеличивается (для исходных нанотрубок без GOx такой эффект отсутствует).

Практическая часть.

Задание

Построить структурную модель углеродной нанотрубки с металлическими и полупроводниковыми свойствами с заданными индексами хиральности (n,m).

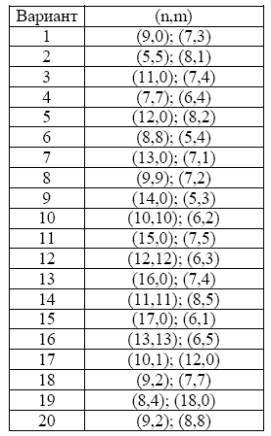
Порядок выполнения работы:

1) Рассчитать угол хиральности углеродных нанотрубок.

2) Рассчитать диаметр углеродных нанотрубок.

3) Определить структурный тип углеродных нанотрубок.

4) Рассчитать элементарную ячейку данной нанотрубки

5) Определить какими свойствами обладает данная нанотрубка.

6) На основе полученных результатов изготовить модель углеродной нанотрубки, используя бумажную модель графенового слоя.

Пример 1.

Модель кресельной нанотрубки

Индексы хиральности нанотрубки (6,6).

1) Угол хиральности рассчитываем по формуле:

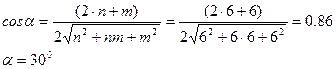
2) Диаметр нанотрубки (6,6) рассчитаем по формуле:

.

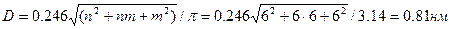3) Данная нанотрубка имеет индексы хиральности (6,6), т.е. n=m, следовательно, она относится к кресельным.

4) Для кресельных нанотрубок ширина ячейки (рис. 1.1) равна величине элементарного вектора а графитовой сетки - 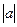=0.246 нм. Величина вектора С равна:

.

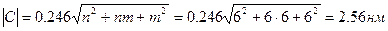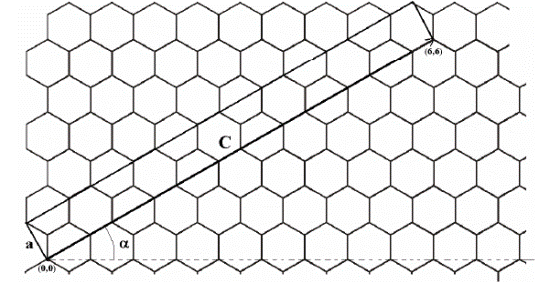
Рис. 1.1. Графеновый слой с элементарной ячейкой для кресельной трубка (6,6 ).

5) Все кресельные нанотрубки обладают металлическими свойствами.

Пример 2.

Модель зигзагной нанотрубки.

Индексы хиральности нанотрубки (10,0).

1) Угол хиральности рассчитываем по формуле:

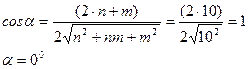
2) Диаметр нанотрубки (10,0) рассчитаем по формуле:

.

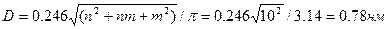3) Данная нанотрубка имеет индексы хиральности (10,0), т.е. m=0, следовательно, она относится к зигзагным.

4) Для зигзагных нанотрубок ширина ячейки (рис. 1.2) равна

.

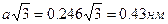Величина вектора С равна: .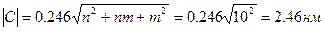

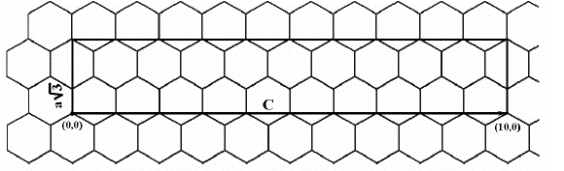
Рис. 1.2. Графеновый слой с элементарной ячейкой для зигзагной трубки (10,0).

5) Индекс хиральности n=10 не кратен 3, следовательно, данная нанотрубка обладает полупроводниковыми свойствами.

Пример 3.

Модель хиральной нанотрубки

Индексы хиральности нанотрубки (5,1).

1) Угол хиральности рассчитываем по формуле:

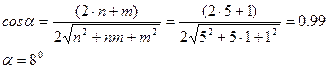
2) Диаметр нанотрубки (5,1) рассчитаем по формуле:

.

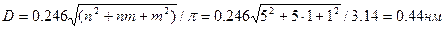3) Данная нанотрубка имеет индексы хиральности (5.1), следовательно она относится к хиральным.

4)Для хиральной нанотрубки (5,1) ширина ячейки (рис. 1.3) определяемся следующим образом: n-m≠3d_н , где d_н наибольший делитель для индексов n и m. В нашем случае 5-1≠3 (наибольший делитель для 5 и 1 будет 1). Ширина ячейки:

.

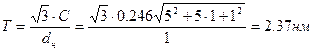Величина вектора С равна:

.

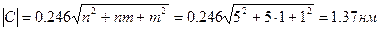5) Разность индексов хиральности n-m=5-1=4 не кратна 3. следовательно, данная нанотрубка обладает полупроводниковыми свойствами.

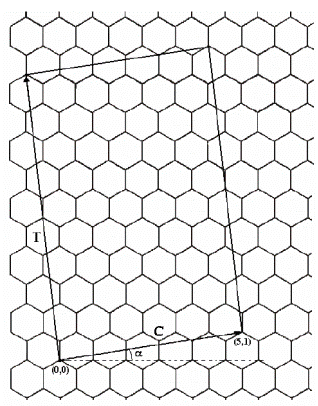
Рис. 1.3. Графеновый слой с элементарной ячейкой для хиральной трубки (5,1).