Принципиально так же решаются задачи измерения напряженности магнитных полей и сил, действующих со стороны этих полей на движущиеся электрические заряды.

Частным случаем движения зарядов является электрический ток в металлических проводниках. То есть, при помощи динамометров можно измерять и силы взаимодействия между электрическими токами, текущими в жестких отрезках проводов, но только для этого нужно прикрепить динамометры к отрезкам проводов. (+ закон Ампера, Ленца). …………

Поместив в магнитное поле, созданное электромагнитом, жесткий отрезок провода и пропуская по нему ток определенной силы можно, при помощи прикрепленных к отрезку провода динамометров, определить величину и направление силы F, действующей на ток со стороны магнитного поля. При этом нужно проводники, подводящие ток к отрезку провода, взять достаточно мягкими и расположить их так, чтобы с их стороны на жесткий отрезок провода не действовали упругие силы. Длину жёсткого провода следует взять достаточно малой, то есть такой, чтобы магнитное поле, действующее на все точки провода, можно было считать одинаковым). Эту силу, обусловленную движением электрических зарядов в отрезке провода, можно выразить через величину и скорость зарядов, образующих ток I.

F = e×[v×H] (12)

Выражение получено из рассмотрения частного случая движения электрических зарядов в металлическом проводнике.

Если электрический заряд движется в пространстве, где одновременно существуют и электрическое и магнитное поля, то на него действуют одновременно две силы: со стороны электрического поля и со стороны магнитного поля. Следовательно, результирующая сила, действующая на заряд,

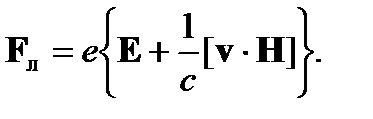(13)

Это - сила Лорентца.??? Такое объединение двух сил, действующих со стороны электрического и магнитного полей, в единую силу Лорентца не является формальным. Сила, определяемая этим выражением, является по своей природе единой силой, и, наоборот, разделение ее на две силы, из которых одна действует со стороны электрического, а другая - со стороны магнитного поля, носит условный характер.

Изучая движение электронов в магнитных полях, можно установить связь между ускорением и силой, действующей на электрон со стороны магнитного поля.

При помощи подобных опытов можно определить удельный заряд электрона и других электрически заряженных частиц, например протонов (ядер водорода), a-частиц (ядер гелия). В этих опытах вместо электронно-лучевой трубки нужно пользоваться источниками, испускающими соответственно протоны или a-частицы с не слишком большими скоростями. Отметим, кстати, что опыты по определению удельного заряда различных частиц являются одним из важнейших методов определения природы этих частиц (так называемая, масс-спектрография).

Псевдосилы

Очередной тип сил, который нам предстоит рассмотреть, — это псевдосилы.

Примером псевдо- (как бы-, вроде-) силы является хорошо известная «центробежная сила». Наблюдатель во вращающейся системе координат (во вращающемся ящике) обнаружит таинственные силы, не вызываемые ни одним из известных источников сил; они отбрасывают предметы к стенке ящика. А объясняются они просто тем, что у наблюдателя; нет ньютоновой системы координат — простейшей из всех.

Псевдосилы обнаруживаются на любопытном опыте, состоящем в том, что мы толкаем с ускорением кувшин с водой, по столу. Тяжесть действует на воду вниз, но из-за горизонтального ускорения есть еще и псевдосила в горизонтальном направлении, назад по отношению к ускорению. Сумма силы, тяжести и псевдосилы образует угол с вертикалью, во время ускорения поверхность воды перпендикулярна к этой сумме сил, т. е. наклонена под углом к столу, и вода приподнята к задней стенке кувшина. Когда мы перестаем толкать кувшин, когда он замедляется вследствие трения, псевдосила меняет свое направление и вода приливает к передней стенке-кувшина (фиг. 12.4).

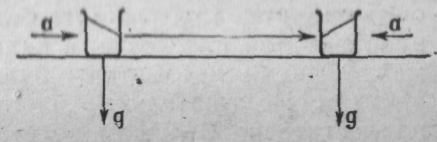
Фиг. 12.4. Иллюстрация к псевдосилам.

Очень важным свойством псевдосил следует считать то, что они всегда пропорциональны массам; то же справедливо и для тяжести. Существует поэтому возможность, что тяжесть — это тоже псевдосила. Не может ли статься, что тяготение вызывается отсутствием правильной системы координат? Ведь мы всегда можем получить силу, пропорциональную массе, стоит только представить, что тело ускоряется. Например, человек, помещенный в ящик, который стоит на земле, обнаруживает, что его что-то прижимает к полу с силой, пропорциональной его массе. Если бы земли не было вовсе, а ящик все еще покоился, то человек плавал бы в пространстве. С другой стороны, если бы опять не было земли, а ящик кто-то тащил бы вверх с ускорением g, то человек в ящике, анализируя физику этого явления, обнаружил бы псевдосилу, прижимающую его к полу точно так же, как это делает тяжесть.

Эйнштейн выдвинул знаменитую гипотезу, что ускорение вызывает имитацию (подобие) тяготения, что силы ускорения (псевдосилы) нельзя отличить от сил тяготения; нельзя сказать, какая часть данной силы — тяжесть, а какая — псевдосила.

Казалось бы, ничто не мешает считать тяжесть псевдосилой, говорить, что нас прижимает вниз оттого, что нас ускоряет вверх; но как быть с жителями Новой Зеландии, на другой стороне Земли — их-то куда ускоряет? Эйнштейн понял, что тяготение можно считать псевдосилой одновременно только в одной точке; его рассуждения привели к предположению, что геометрия мира сложнее обычной геометрии Евклида. Наше обсуждение вопроса чисто качественное и не претендует ни на что, кроме общей идеи.

Чтобы пояснить в общих чертах, как тяготение может быть результатом действия псевдосил, мы приведем чисто геометрический пример, ничего общего не имеющий с истинным положением вещей. Предположим, что мы с вами обитаем в двумерном мире и ничего о третьем измерении не знаем. Мы бы считали, что живем на плоскости, а на самом деле, предположим, жили бы на шаре; пускай теперь мы бросили предмет вдоль нашей поверхности, не действуя больше на него никакими силами. Как бы он двигался? Нам, казалось бы, что он движется по прямой линии, но поскольку третьего измерения нет и он должен был бы оставаться на поверхности шара, то он двигался бы по кратчайшему расстоянию на сфере, т. е. по окружности большого круга. Бросим точно так же другой предмет, но в ином направлении; он направится тоже по дуге большого круга. Мы думаем, что находимся на плоскости, и надеемся поэтому, что расстояние между двумя предметами будет расти линейно с течением времени. Но тщательные наблюдения вдруг обнаружат, что на достаточно большом расстоянии предметы снова начнут сближаться, как если бы они притягивали друг друга. Но они не притягиваются один к другому; все дело в геометрии, это с нею происходит что-то «чудное». Хотя эта картинка и не касается геометрии Евклида (не показывает нам, что в ней есть «чудного»), но она показывает, что, заметно исказив геометрию, можно все тяготение отнести за счет псевдосилы. В этом и состоит общая идея теории тяготения Эйнштейна.

Ядерные силы

Мы заключим эту главу кратким обзором единственных ныне известных сил, отличающихся от перечисленных, — ядерных сил. Эти силы действуют внутри ядра атома, и, хотя их много изучали, никто ни разу еще не смог рассчитать силу, действующую между двумя ядрами; и фактически закон ядерных сил сейчас не известен. Эти силы имеют крайне незначительную протяженность действия — они действуют только на размерах ядра около 10^{-13 см. Поскольку частицы столь малы, а расстояния так коротки, нам нечего надеяться на законы Ньютона — здесь действуют только законы квантовой механики. Анализируя ядра, мы больше не говорим о силах; мы заменяем понятие силы понятием энергии взаимодействия двух частиц (позже об этом будет сказано подробнее). Любые формулы, которые можно написать для ядерных сил, представляют довольно грубые приближения, в которых опущены многие детали взаимодействия; выглядят они примерно так: силы внутри ядер убывают не обратно квадрату расстояния, а отмирают экспоненциально за некоторым расстоянием} r₀ (порядка 10^{-13 см) как} F=(1/r²)·ехр(-r/r_о). Иначе говоря, чуть частицы удалятся, как силы тут же исчезают, хотя ближе 10^{-13 см они очень велики. По-видимому, законы ядерных сил сложны до чрезвычайности; мы их не понимаем, и вся задача анализа фундаментального механизма, стоящего за ними, не решена. Попытки решить, эту задачу привели к открытию множества необычных частиц, например π-мезонов, но происхождение сил все равно остается темным.}

2.2.5. Измерение тепловых величин

(Количества вещества, концентрации, теплопроводности)

2.2.6. Измерение акустических величин

(звукового давления, объемной скорости, интенсивности звука).

2.2.7. Измерение световых величин и величин электромагнитных излучений

(Атомные процессы. …..)

(силы света, светового потока, освещённости, яркости, энергии излучения, потока излучения, яркости)

2.2.8. Измерение величин физической оптики

(оптических параметров и характеристик теплового излучения)

2.2.9. Измерение величин ионизирующих излучений

(активности нуклида радиоактивного источника, дозы поглощённого излучения)