Электромагнитная волна в диэлектрике.

Решение волнового уравнения для плоских волн.

Для этого случая считаем, что источники бесконечно удалены и поэтому правые части волновых уравнений равны нулю.

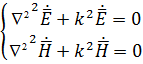
Решение этих уравнений производится в прямоугольной системе координат, так как только в этой системе координатные поверхности являются плоскими.

Решением этой системы уравнений являются

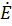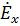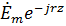= = (5)

= =

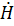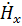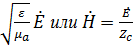
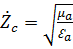- волновое сопротивление среды.

Векторы 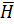и 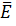плоской волны взаимно перпендикулярны.

Вектор Пойтинга направлен параллельно оси OZ и равен

= =

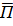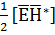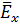
Электромагнитная волна в диэлектрике.

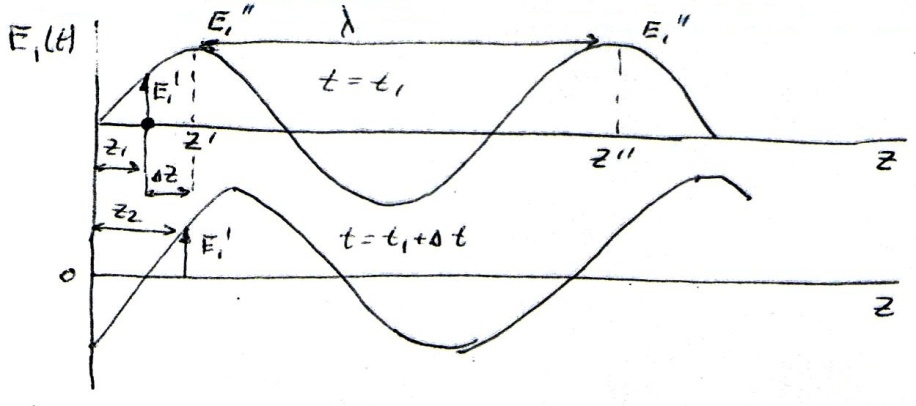
В некоторый момент времени t1напряженность электрического поля волны распределена по оси Z косинусоидально

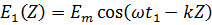
По прошествии времени Δt волна переместится вправо по оси OZ на расстояние ΔZ. Величина напряженности 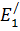… имевшее место в точке Z1, теперь будет в точке Z2=Z1+ .

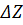Для этих точек будет справедливо равенство.

..

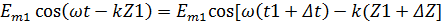Откуда получаем равенство фаз

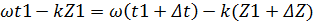или

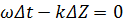
Отсюда находим 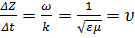. . Так как величина υ найдена из условия перемещения точек постоянной фазы то она представляет собой фазовую скорость.

Длина волны в диэлектрике определяется как расстояние на которое переместится волна при котором в момент времени t₁ фаза изменится на 2π. Отсюда можно записать указанные изменения фазы

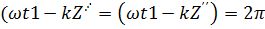…. или

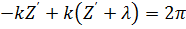….. отсюда

…

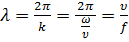Структура электромагнитной волны в пространстве для диэлектрической среды имеет вид

…. ….. …

…. …. …

В случае диэлектрика …. – действительное число, поэтому … и … совпадают по фазе.

Мгновенное значение вектора Пойнтинга имеет вид

……..

Электромагнитная волна в полупроводящей среде

В случае среды с конечной проводимостью … - величина комплексная.

………….

где ……………….. –коэффициент фазы или волновое число:

…………….. – коэффициент затухания (поглощения)

Отметим, что для случая диэлектрика … (проводимость)…. (затухания нет), а ….. .

Окончательно

….

….

где ….. – модуль волнового сопротивления среды

…. – аргумент волнового сопротивления среды.

………..

…………

……………..

Из приведенных формул следует, что при распространении в среде с конечной проводимостью электромагнитная волна ослабляется (затухает при увеличении расстояния). Затухание амплитуд напряженности определяется множителем … , то есть коэффициентом затухания. Фазовая скорость

………….

Структура поля волны предустновлена двумя взаимно перпендикулярными гармоническими колебаниями, не совпадающими по фазе (волна H сдвинута в пространстве относительно волны Е на расстояние …, где … - аргумент волнового сопротивления).

Мгновенное значение вектора Пойнтинга

…………………….

Структура волны в диэлектрике имеет вид

………………..

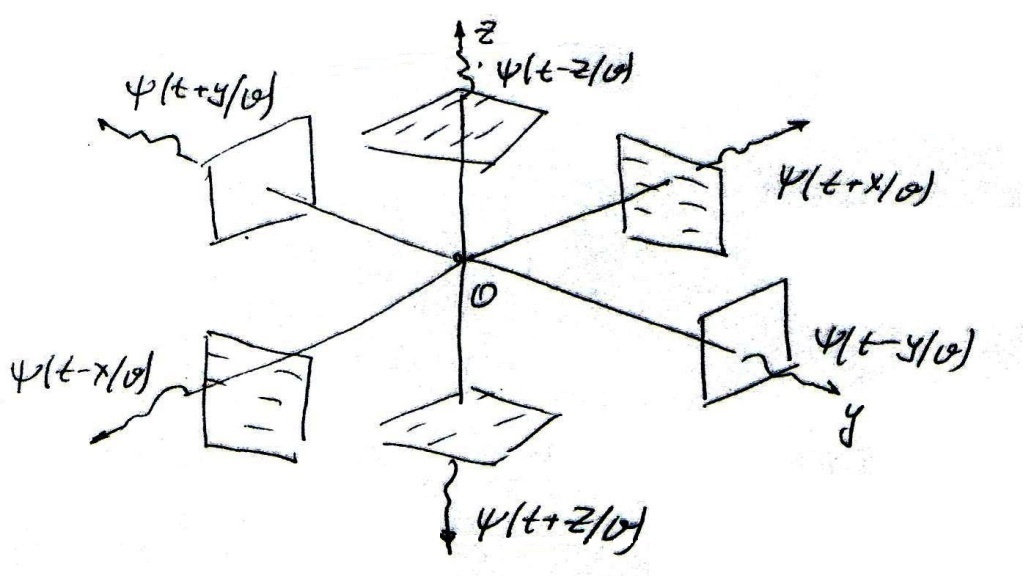где под Z можно подразумевать любую из величин 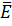, , 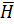, 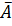ϕ_СК, a I_z- источник.

Полученное уравнение относится к классу неоднородных линейных уравнений в частных производных второго порядка гиперболического типа.

Выражение

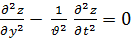(8)

Является однородным волновым уравнением ( например, описывающим колебания бесконечной струны, натянутой вдоль У) Решением (8) являются плоские волны Z , бегущие со скоростью…. В направлении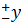

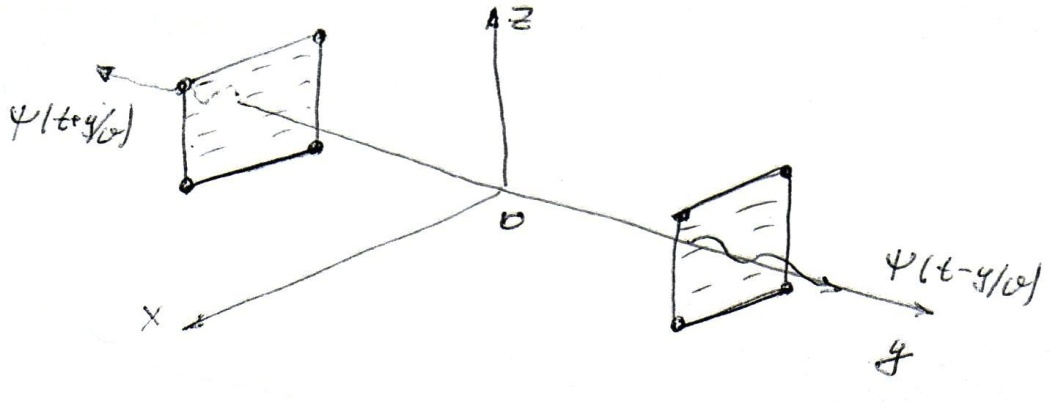
Двумерное уравнение.

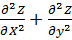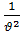
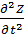( )- =0 Z- это не ось координат, а аналог 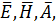ϕ_ск

Имеет своим решением бесконечный набор пар плоских волн типа ϕ( 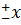(ϑ), ϕ(t 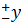(ϑ))) бегущих в любых направлениях в плоскости XOY( цилиндрическая волна)

Решением трехмерного уравнения

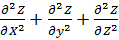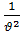
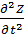( )- =0

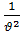
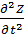ΔZ- =0

Является трехмерная ( сферическая) волна ϕ(t- 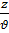) складывающаяся из бесконечного набора пар плоских волн, разбегающихся из начала трехмерной системы координат XYZ во всех направлениях.

Если источники поля распределены в конечном объеме V, то

Z(z,t)= 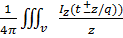dv - набег фазы.

В частности

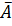(z,t)= 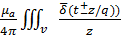dv

ϕ_ск(z,t)= 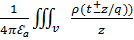dv

Таким образом , любое возмущение состояния электромагнитного поля приводит к появлению сферических волн ϕ, которые разбегаются со скоростью ϑ во всех направлениях от источника.

Скоростью распространения электромагнитной волны определяется параметрами той среды, в которой она распространяется.

ϑ=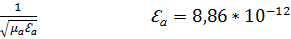

ϑ=е=3*10^-8м/с μ_а²=4π*10^-7