Магнитное поле в веществе. Магнитный гистерезис. Электромагнитная индукция. Энергия магнитного поля. Основы теории электромагнитного поля.

Магнитное поле в веществе

Для качественного объяснения магнитных явлений с достаточным приближением можно считать, что электрон движется в атоме по круговым орбитам. Электрон, движущийся по одной из таких орбит, эквивалентен круговому току, поэтому он обладает орбитальным магнитным моментом 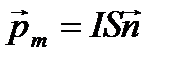, модуль которого

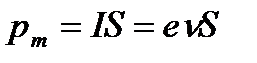, (29)

где 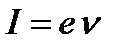– сила тока, n - частота вращения электрона по орбите, S – площадь орбиты.

Магнитным моментом атома называется вектор, равный геометрической сумме орбитальных моментов всех электронов атома:

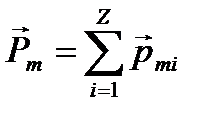, (30)

где Z – число электронов в атоме, равное порядковому номеру элемента в системе Менделеева.

Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность J, равная отношению магнитного момента макроскопически малого объема вещества к этому объему:

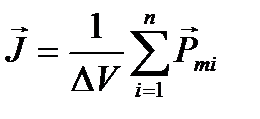, (31)

где P_mi – магнитный момент i-го атома (молекулы) из общего числа n атомов (молекул), содержащихся в объеме DV.

Магнитное поле в веществе складывается из двух полей: внешнего поля В₀ и поля, создаваемого намагниченным веществом B’ , т.е.

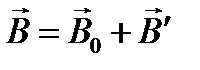, где .

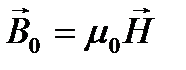Поле в веществе же определится 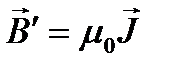, т.е. .

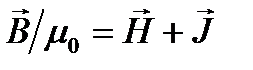Как показывает опыт, в несильных полях намагниченность прямо пропорциональна напряженности поля, вызывающего намагничение, т.е. 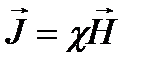, где c – безразмерная величина, называемая магнитной восприимчивостью вещества. Тогда можно написать выражение (1) в виде:

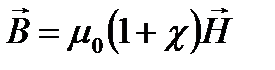, (32)

где безразмерная величина 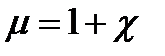представляет собой магнитную проницаемость вещества.

Все вещества при рассмотрении их магнитных свойств принято называть магнетиками. По своим магнитным свойствам магнетики подразделяются на три основные группы: диа-, пара- и ферромагнетики.

1) Диамагнетиками называются вещества, которые намагничиваются во внешнем магнитном поле в направлении, противоположном направлению вектора магнитной индукции поля. К ним относятся инертные газы, висмут, цинк, медь, золото, кремний, большинство органических соединений.

2) Парамагнетики – вещества, намагничивающиеся во внешнем магнитном поле по направлению поля. К ним относятся многие щелочные и переходные металлы, их сплавы и оксиды. Абсолютное значение магнитной восприимчивости для диа- и парамагнетиков очень мало (порядка 10^-4 – 10^-6), поэтому для них m незначительно отличается от единицы. Но для диамагнетиков c<0 и m<1, для парамагнетиков c>0 и m>1.

3) Ферромагнетиками называются твердые вещества, обладающие при не слишком высоких температурах самопроизвольной (спонтанной) намагниченностью, которая сильно изменяется под влиянием внешних воздействий – магнитного поля, деформации, изменения температуры. К ним относят железо, кобальт, никель, ряд сплавов, ферриты.

Магнитный гистерезис

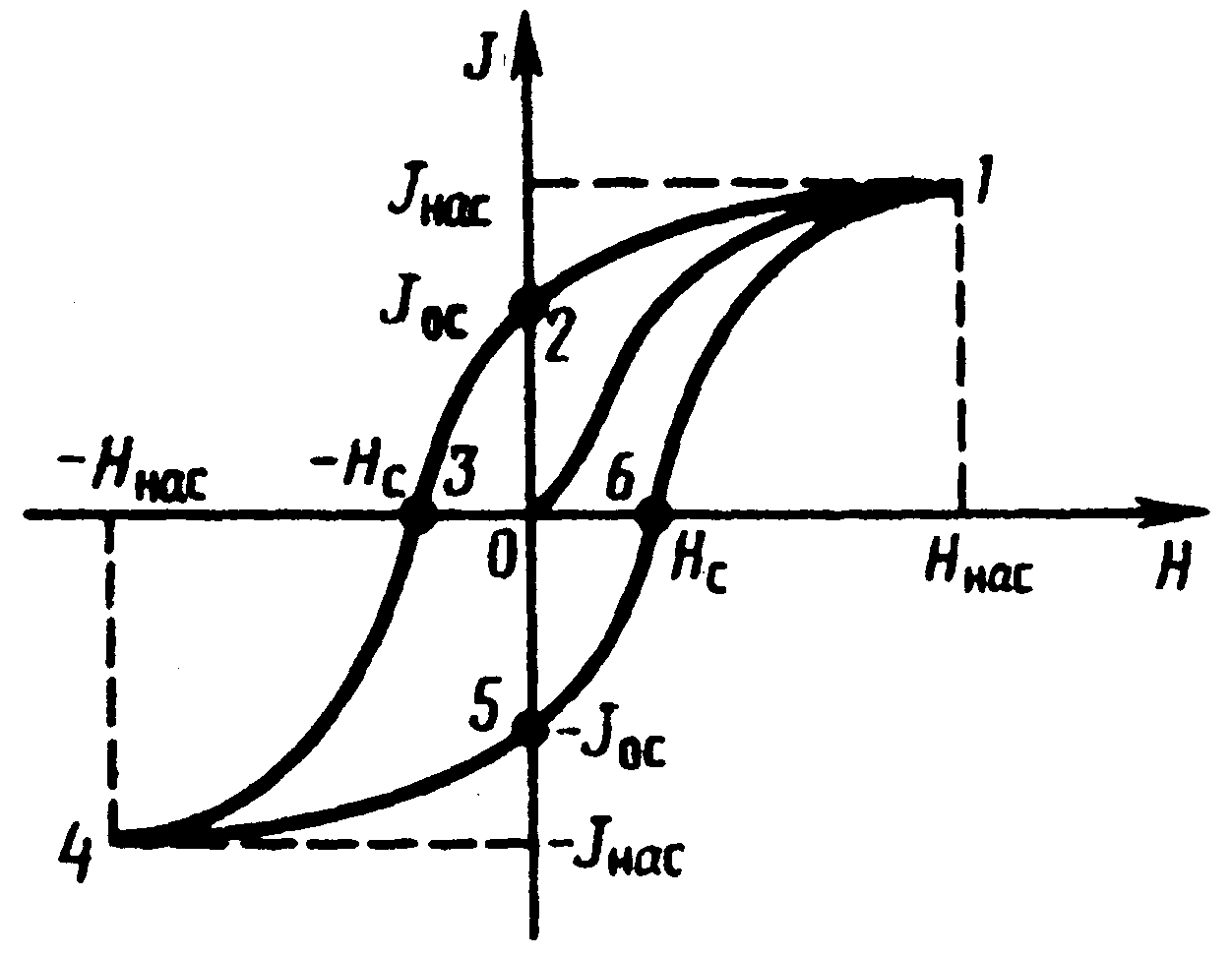Рис. 13

У ферромагнетиков наблюдается явление магнитного гистерезиса – нелинейная зависимость намагниченности образца от напряженности внешнего магнитного поля. Иллюстрирующий его график приведен на рис. 13. Здесь участок 0-1 является начальной кривой намагничивания – зависимости изменения намагниченности полностью размагниченного образца от напряженности внешнего поля. Точка 1 называется магнитным насыщением, после которого при дальнейшем увеличении внешнего поля намагниченность образца не изменяется. Если после достижения точки 1 внешнее поле начинает постепенно уменьшаться до нуля, то в ферромагнетике наблюдается остаточная намагниченность (точка 2). Чтобы полностью размагнитить образец необходимо подвести поле, имеющее направление, противоположное полю, вызвавшему намагничение. Напряженность Н_С называется коэрцитивной силой (точка 3). При дальнейшем увеличении противоположного поля ферромагнетик перемагничивается (кривая 3-4), достигает насыщения (точка 4). Затем ферромагнетик можно опять размагнитить (кривая 4-5-6) и вновь перемагнитить до насыщения (кривая 6-1). Полученная кривая 1-2-3-4-5-6 называется петлей гистерезиса.

Для каждого ферромагнетика имеется определенная температура, называемая точкой Кюри, при которой он теряет свои магнитные свойства. При этом у него изменяются и некоторые другие физические свойства – теплоемкость, электропроводность и т.д. Выше точки Кюри ферромагнетик ведет себя во внешнем магнитном поле как парамагнитное вещество.

Согласно классической теории ферромагнетизма, весь объем ферромагнитного образца при температуре ниже точки Кюри разбит на небольшие области – домены, которые самопроизвольно (спонтанно) намагничены до насыщения. Линейные размеры доменов порядка 10^-3-10^-2 см. в размагниченном образце в отсутствие внешнего магнитного поля магнитные моменты доменов ориентированы так, что результирующая намагниченность образца в целом равна нулю. Намагничивание такого образца в магнитном поле, напряженность которого медленно и монотонно увеличивается, происходит за счет двух процессов: смещения границ доменов и вращения магнитных моментов доменов. Процесс смещения границ между доменами приводит к росту размеров тех доменов, которые самопроизвольно намагничены в направлениях, близких к направлению вектора Н. Процесс вращения магнитных моментов доменов по направлению Н играет основную роль только в области, близкой к насыщению.

Ферромагнетики с малой (0,001 – 1 А/см) коэрцитивной силой (с узкой петлей гистерезиса) называются магнито-мягкими, а с большой (10 – 10000 А/см) коэрцитивной силой (с широкой петлей гистерезиса) – магнито-твердыми материалами. Магнито-мягкие используют обычно для изготовления сердечников трансформаторов, а магнито-твердые – для создания постоянных магнитов.

Существует два магнитомеханических эффекта:

1) явление магнитострикции, состоящее в изменении формы и размеров ферромагнитного образца при его намагничивании;

2) эффект Виллари, состоящий в изменении намагниченности ферромагнитного образца при его механической деформации.

Эти явления применяются в магнитострикционных датчиках и реле. Механические колебания, возникающие в ферромагнетиках при их намагничивании в периодически изменяющемся магнитном поле, используются в магнитострикционных излучателях ультразвука.

В последнее время большое значение приобрели полупроводниковые ферромагнетики – ферриты, химические соединения типа МеО×Fe₂O₃, где Ме – ион двухвалентного металла (Mn, Co, Ni, Cu, Mg, Zn, Cd, Fe). Они отличаются заметными ферромагнитными свойствами и большим удельным электрическим сопротивлением. Ферриты применяются для изготовления постоянных магнитов, ферритовых антенн, сердечников радиочастотных контуров, элементов оперативной памяти, для покрытия пленок в магнитофонах и т.д.

Электромагнитная индукция.

Явление электромагнитной индукции заключается в том, что в замкнутом проводящем контуре при изменении потока магнитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного. Рассмотрим классические опыты Фарадея, с помощью которых было обнаружено явление электромагнитной индукции.

Опыт 1. Если в замкнутый на гальванометр соленоид вдвигать и выдвигать постоянный магнит, то в моменты его вдвигания или выдвигания наблюдается отклонение стрелки гальванометра (возникает индукционный ток); направления отклонения стрелки при вдвигании и выдвигании магнита противоположны. Отклонение стрелки гальванометра тем больше, чем больше скорость движения магнита относительно катушки.

Опыт 2. Концы одной из катушек, вставленных одна в другую, присоединяются к гальванометру, а через другую катушку пропускается ток. Отклонение стрелки гальванометра наблюдается в моменты включения и выключения тока, в моменты его увеличения или уменьшения или при перемещении катушек друг относительно друга. Направления отклонений стрелки гальванометра также противоположны при включении или выключении тока, его увеличении или уменьшении, сближении или удалении катушек.

Фарадей показал, что всякий раз, когда происходит изменение сцепленного с контуром потока магнитной индукции, в контуре возникает индукционный ток; его возникновение указывает на наличие в цепи электродвижущей силы, называемой электродвижущей силой электромагнитной индукции. Закон электромагнитной индукции Фарадея гласит: какова бы ни была причина изменения потока магнитной индукции, охватываемого замкнутым проводящим контуром, возникающая в контуре ЭДС

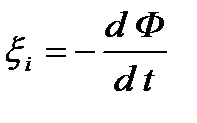. (33)

Здесь знак минус определяется правилом Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызвавшему индукционный ток.

Какова природа электромагнитной индукции? Если проводник (подвижная перемычка на рис. 7) движется в постоянном магнитном поле, то сила Лоренца, действующая на заряды внутри проводника, движущиеся вместе с проводником, будет направлена противоположно току, т.е. она будет создавать в проводнике индукционный ток противоположного направления.

Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в переменное магнитное поле. Эти токи оказываются замкнутыми в толще проводника и поэтому называются вихревыми или токами Фуко. Вихревые токи вызывают нагревание проводников, поэтому для уменьшения потерь якоря генераторов и сердечники трансформаторов делают не сплошными, а изготовляют из тонких пластин, отделенных одна от другой слоями изолятора, и устанавливают их так, чтобы токи Фуко были направлены поперек пластин.

11. Самоиндукция, взаимная индукция, индуктивность, трансформаторы

Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I в контуре:

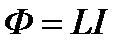, (34)

где коэффициент пропорциональности L называется индуктивностью контура. Единица индуктивности в СИ – генри (Гн).

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно в контуре будет индуцироваться ЭДС. Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией. Применяя к явлению самоиндукции закон Фарадея, получим

.

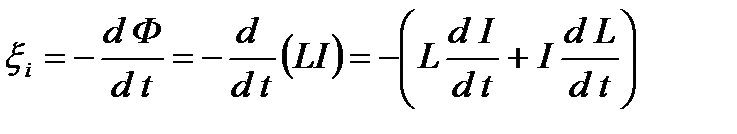Если контур не деформируется и магнитная проницаемость среды не изменяется, то L=const и

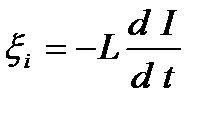, (35)

где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения тока в нем.

Явление возникновения ЭДС в одном из близкорасположенных контуров при изменении силы тока в другом называется взаимной индукцией. Если в контуре 1 изменяется ток I₁, то в контуре 2 индуцируется ЭДС x_i2, которая по закону Фарадея равна и противоположна по знаку скорости изменения магнитного потока Ф₂₁, созданного током в первом контуре и пронизывающего второй:

.

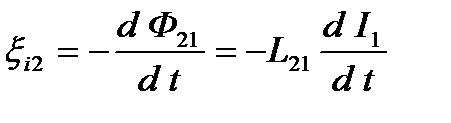Аналогично, если в контуре 2 изменяется ток I₂, то в контуре 1 индуцируется ЭДС x_i1, которая по закону Фарадея равна и противоположна по знаку скорости изменения магнитного потока Ф₁₂, созданного током во втором контуре и пронизывающего первый:

.

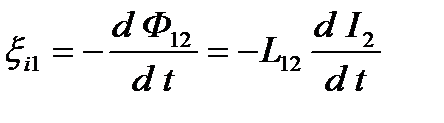Коэффициенты пропорциональности L₁₂ и L₂₁ называются взаимной индуктивностью контуров. Расчеты, подтверждаемые опытом, показывают, что L₁₂=L₂₁.

Индуктивность соленоида определяется по формуле:

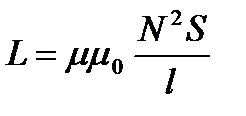, (36)

где N – число витков соленоида, l – его длина, S – площадь сечения, m – магнитная проницаемость вещества, из которого сделан сердечник соленоида. Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится.

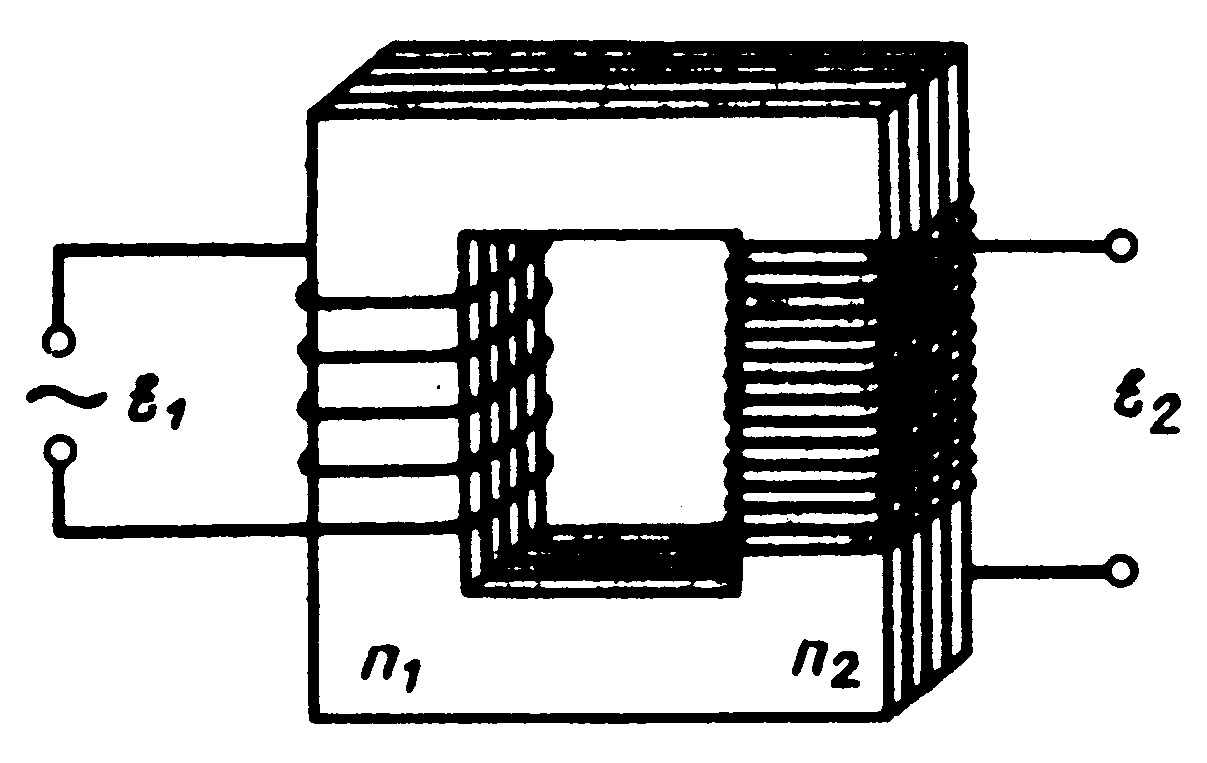Рис. 14

Полный магнитный поток, сцепленный со всеми витками соленоида, называется потокосцеплением

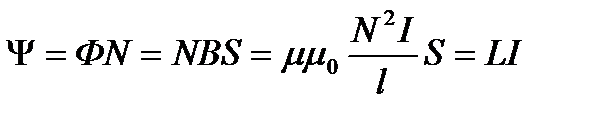. (37)

Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Принципиальная схема трансформатора приведена на рис. 14. Первичная и вторичная катушки (обмотки), имеющие соответственно N₁ и N₂ витков, укреплены на замкнутом железном сердечнике. При пропускании через первичную катушку переменного тока во вторичной обмотке возникает ЭДС

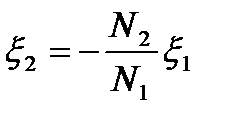, (38)

где знак минус показывает, что ЭДС в первичной и вторичной обмотках противоположны по фазе. Отношение числа витков N₁/N₂ называется коэффициентом трансформации. Пренебрегая потерями энергии, можно показать, что токи в обмотках обратно пропорциональны числу витков в этих обмотках. Если N₁/N₂>1, то имеем дело с повышающим трансформатором, а если N₁/N₂<1, то – с понижающим.

Энергия магнитного поля

Магнитное поле является носителем энергии. Энергия магнитного поля равна работе, которая затрачивается током на создание этого поля. Работа контура индуктивностью L с током I определится 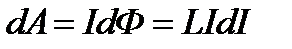. Тогда работа по созданию магнитного потока Ф будет равна

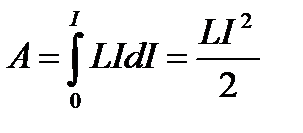
Следовательно, энергия магнитного поля, связанного с контуром,

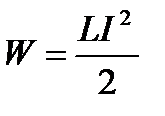. (39)

Рассмотрим однородное магнитное поле внутри соленоида. Подставив в (39) выражение (36), получим

.

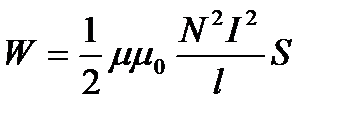Т.к. 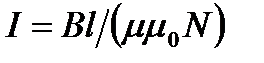(по формуле 15) и 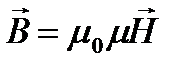(по формуле 1), то

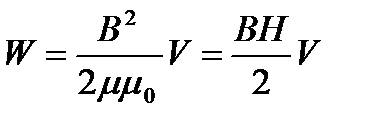, (40)

где 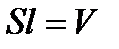– объем соленоида.

Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью

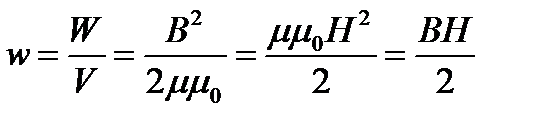. (41)

Это выражение справедливо только для сред, для которых зависимость В от Н линейная, т.е. только для пара- и диамагнетиков.

Основы теории электромагнитного поля.

Законченную теорию электромагнитного поля разработал Д. Максвелл. В теории Максвелла решается основная задача электродинамики: найти характеристики электромагнитного поля заданной системы электрических зарядов и токов. В теории Максвелла не рассматриваются молекулярное строение среды и внутренний механизм процессов, происходящих в среде в электромагнитном поле. Электрические и магнитные свойства среды характеризуются тремя величинами: относительной диэлектрической проницаемостью, относительной магнитной проницаемостью и удельной электрической проводимостью. В теории Максвелла рассматриваются макроскопические электромагнитные поля макроскопических зарядов и токов.

Закон Фарадея (формула 33) не указывает на причину возникновения индукционного тока. Согласно Максвеллу всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре. Максвелл доказал, что циркуляция вектора напряженности такого порождаемого поля не равна нулю, в отличии от циркуляции вектора напряженности электростатического поля. Следовательно, электрическое поле, возбуждаемое магнитным полем, как и само магнитное поле, является вихревым.

Максвелл ввел понятие тока смещения. Именно ток смещения является той частью тока проводимости, которая создает в окружающем пространстве магнитное поле. Математически ток смещения выражается с помощью понятия электрическое смещение, известного из раздела «электрическое поле в диэлектрике»:

,

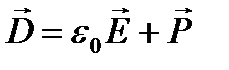где Е – напряженность поля, Р – поляризованность диэлектрика, характеризующее смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах. Плотность тока смещения в диэлектрике выразится

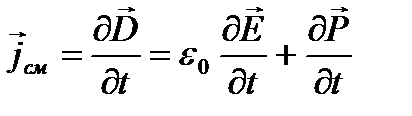. (42)

Максвелл ввел также понятие полного тока, равного сумме токов проводимости и смещения. Плотность полного тока

.

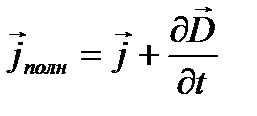Максвелл обобщил теорему о циркуляции вектора Н (формула 14), введя в ее правую часть полный ток 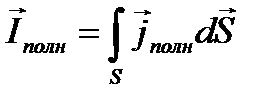сквозь поверхность S, натянутую на замкнутый контур L. Тогда обобщенная теорема о циркуляции вектора Н (закон полного тока) запишется в виде

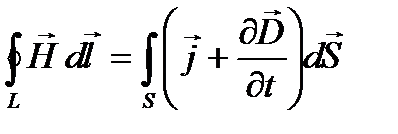. (43)

Уравнения Максвелла.

Обобщая положения и понятия, приведенные выше, Максвелл вывел четыре уравнения, которые лежат в основе теории.

1. Электрическое поле может быть как потенциальным, так и вихревым. Циркуляция вектора напряженности суммарного поля

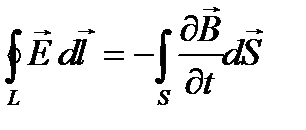(44)

Это первое уравнение Максвелла показывает, что циркуляция вектора напряженности электрического поля по произвольному неподвижному замкнутому контуру, мысленно проведенному в электромагнитом поле, равна взятой с обратным знаком скорости изменения магнитного потока через поверхность S, натянутую на этот контур. Таким образом источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н является вторым уравнением Максвелла:

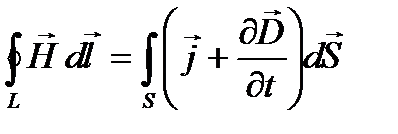. (43)

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорему Остроградского-Гаусса для поля D

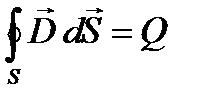(45)

называют третьим уравнением Максвелла, показывающим, что поток смещения через произвольную неподвижную замкнутую поверхность, мысленно проведенную в электромагнитном поле, равен суммарному свободному заряду, который находится внутри этой поверхности. Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью r, то (45) запишется в виде:

.

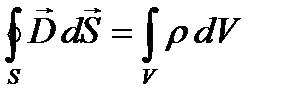4. Теорема Гаусса для поля В

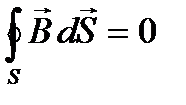(46)

принято считать четвертым уравнением Максвелла.

Выражения (43-46) – есть полная система уравнений Максвелла в интегральной форме. Величины, входящие в эту систему, не являются независимыми и между ними существует определенная связь, которая для случая изотропных несегнетоэлектрических и неферромагнитных сред записывается уже известными формулами:

, , .

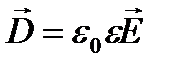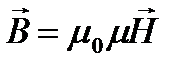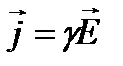Для стационарных полей (E=const и B=const) уравнения Максвелла примут вид:

, , , .

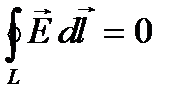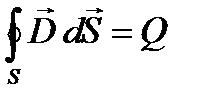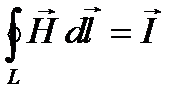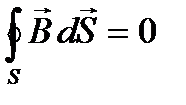Т.е. в данном случае электрические и магнитные поля независимы друг от друга, что позволяет изучать отдельно постоянные электрические и магнитные поля.

Воспользовавшись известными из векторного анализа теоремами Стокса и Гаусса:

, ,

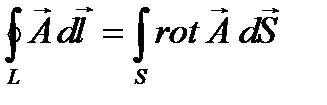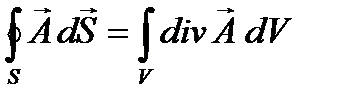где rot A – ротор вектора А, выражающийся в декартовых координатах следующим образом: 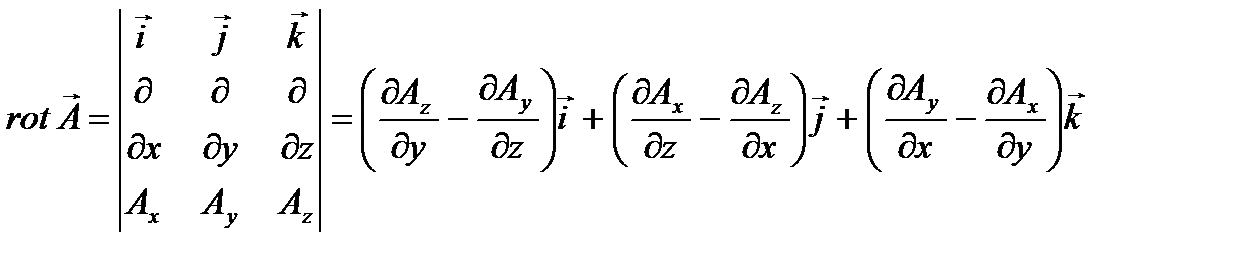; дивергенция вектора А определяется формулой 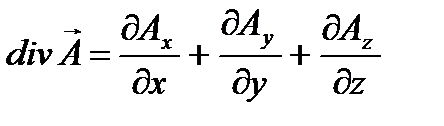, где A_x, A_y, A_z - проекции А на оси координат; можно представить полную систему уравнений Максвелла в дифференциальной форме (характеризующих поле в каждой точке пространства):

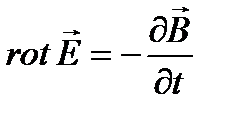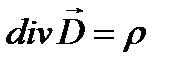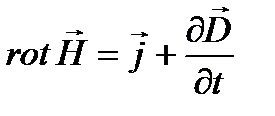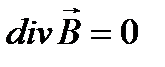; ; ; . (47)

Если заряды и токи распределены в пространстве непрерывно, то обе формы уравнений Максвелла эквивалентны. Однако если имеются поверхности разрыва – поверхности, на которых свойства среды или полей меняются скачкообразно, то интегральная форма уравнений является более общей.

Итак, из уравнений Максвелла следует, что переменное магнитное поле всегда связано с порождаемым им электрическим полем, а переменное электрическое поле всегда связано с порождаемым им магнитным, т.е. электрическое и магнитное поля неразрывно связаны друг с другом – они образуют единое электромагнитное поле. Одним из выводов из теории Максвелла явилось предсказание существования электромагнитных волн – переменного электромагнитного поля, распространяющегося в пространстве с конечной скоростью.