Электрический заряд. Закон Кулона.
Все тела в природе способны электризоваться, т.е. приобретать электрический заряд. Все заряды разделяются на два типа, условно названные положительными и отрицательными. Опытным путем доказано, что электрический заряд дискретен, т.е. заряд любого тела составляет целое кратное от элементарного электрического заряда е (е=1,6×10-19 Кл). Электрон (me= 9,11×10-31 кг) и протон (mp=1,67×10-27 кг) являются соответственно носителями элементарных отрицательного и положительного зарядов.
Из обобщения опытных данных был установлен фундаментальный закон природы – закон сохранения заряда: алгебраическая сумма электрических зарядов замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы не происходили внутри этой системы. Единица электрического заряда – кулон (Кл) – электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с.
В зависимости от концентрации свободных зарядов тела делятся на проводники, диэлектрики и полупроводники. Проводники – тела, в которых электрический заряд может перемещаться по всему объему. Проводники делятся на две группы: 1) проводники первого рода (металлы) – перенос в них зарядов (свободных электронов) не сопровождается химическими превращениями; 2) проводники второго рода (электролиты) – перенос в них зарядов (положительных и отрицательных ионов) ведет к химическим изменениям. Диэлектрики (стекло, пластмассы) – тела, в которых практически отсутствуют свободные заряды. Полупроводники (кремний, германий) занимают промежуточное положение между проводниками и диэлектриками. Указанное деление тел является весьма условным, т.к. сильно зависит от внешних условий.
Закон взаимодействия неподвижных точечных электрических зарядов установлен Кулоном с помощью крутильных весов. Точечным называется заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует. Понятие точечного заряда, как и материальной точки, является физической абстракцией. Итак, закон Кулона: сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме, пропорциональна зарядам Q1 и Q2 и обратно пропорциональна квадрату расстояния r между ними:
 , (1)
, (1)
где k – коэффициент пропорциональности, зависящий от выбора системы единиц.
Сила F направлена по прямой, соединяющей взаимодействующие заряды, т.е. является центральной, и соответствует притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов (рис. 1). Эта сила называется кулоновской силой. В системе СИ коэффициент пропорциональности равен
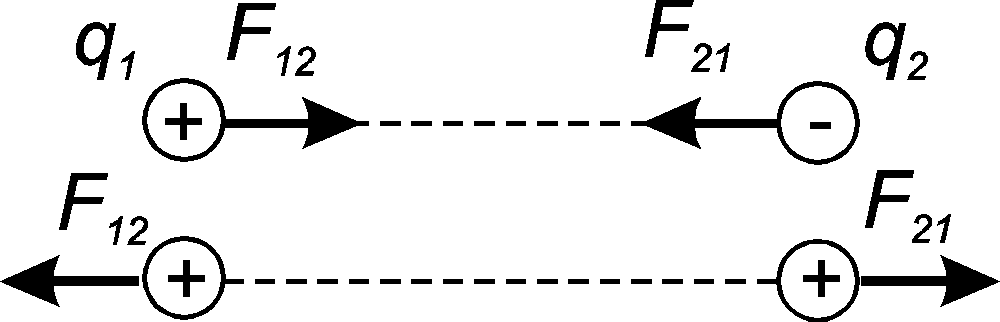 Рис. 1
Рис. 1
|
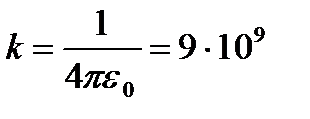 (м/Ф).
(м/Ф).
Здесь величина e0 называется электрической постоянной; она относится к числу фундаментальных физических постоянных и равна e0=8,85×10-12 [Кл2/(Н×м2)] или [Ф/м], где фарад (Ф) – единица электрической емкости.
Всякое заряженное тело можно рассматривать как совокупность точечных зарядов. Однако часто бывает значительно удобнее считать, что заряды распределены в заряженном теле непрерывно. Соответственно рассматривают три случая.
1. Линейная плотность электрических зарядов: 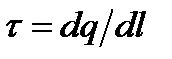 , где dq – заряд малого участка заряженной линии длиной dl.
, где dq – заряд малого участка заряженной линии длиной dl.
2. Поверхностная плотность электрических зарядов: 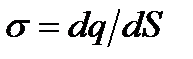 , где dq – заряд малого участка заряженной поверхности площадью dS.
, где dq – заряд малого участка заряженной поверхности площадью dS.
3. Объемная плотность электрических зарядов: 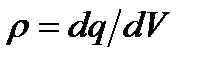 , где dq – заряд малого элемента заряженного тела объемом dV.
, где dq – заряд малого элемента заряженного тела объемом dV.
Напряженность. Поле диполя.
Если в пространство, окружающее электрический заряд, внести другой заряд, то на него будет действовать сила; значит, в пространстве, окружающем электрические заряды, существует силовое поле. Будем рассматривать электрические поля, которые создаются неподвижными электрическими зарядами и называются электростатическими. Для обнаружения и опытного исследования электростатического поля используется пробный точечный положительный заряд – такой заряд, который не искажает исследуемое поле (не вызывает перераспределения зарядов, создающих поле). Если в поле, создаваемое зарядом Q, поместить пробный заряд q, то на него действует сила F, различная в разных точках поля, которая, согласно (1), пропорциональна пробному заряду q. Поэтому отношение F/q не зависит от q и характеризует электростатическое поле в той точке, где пробный заряд находится. Эта величина называется напряженностью и является силовой характеристикой электростатического поля.
Итак, напряженность электростатического поля в данной точке есть физическая величина, определяемая силой, действующей на пробный единичный положительный заряд, помещенный в эту точку поля:
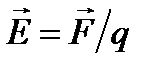 . (2)
. (2)
Как следует из (1) и (2), напряженность поля точечного заряда в вакууме
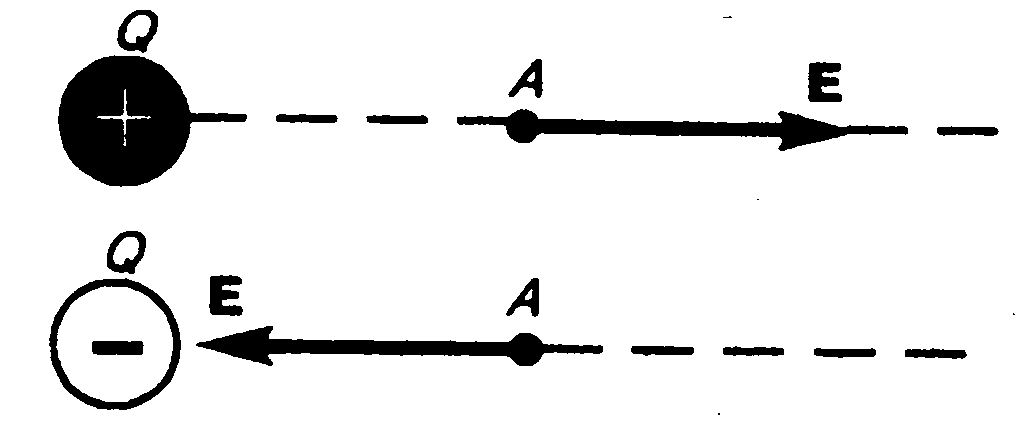 Рис. 2 Рис. 2
|
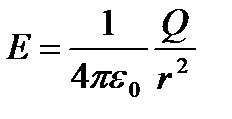 . (3)
. (3)
Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если поле создается положительным зарядом, то вектор Е направлен вдоль радиуса-вектора от заряда во внешнее пространство (отталкивание пробного положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду (рис. 2). В СИ вместо очевидного (Н/Кл) для напряженности принята другая единица измерения (В/м) (вольт/метр).
Графически электростатическое поле изображают с помощью линий напряженности – линий, касательные к которым в каждой точке совпадают с направлением вектора Е. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности – радиальные прямые, выходящие из заряда, если он положителен и входящие в него, если заряд отрицателен.
 Рис. 3
Рис. 3
|
Если электростатическое поле создано системой неподвижных зарядов Q1, Q2, …Qn, то определение модуля и направления вектора напряженности Е в каждой точке электростатического поля подчинено принципу суперпозиции, согласно которому напряженность Е результирующего поля, создаваемого системой зарядов, равна геометрической сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности:
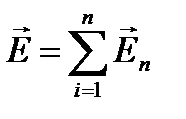 . (4)
. (4)
Принцип суперпозиции позволяет рассчитать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов. Так принцип суперпозиции применим для расчета электростатического поля электрического диполя.
Электрический диполь – система двух равных по модулю разноименных точечных зарядов (+Q, -Q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля. Вектор, направленный по оси диполя (прямой, проходящей через оба заряда) от отрицательного заряда к положительному и равный расстоянию между ними, называется плечом диполя l. Вектор 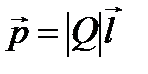 , совпадающий по направлению с плечом диполя и равный произведению заряда Q на плечо l, называется электрическим моментом диполя или дипольным моментом (рис. 3). Определим напряженность поля диполя в двух случаях.
, совпадающий по направлению с плечом диполя и равный произведению заряда Q на плечо l, называется электрическим моментом диполя или дипольным моментом (рис. 3). Определим напряженность поля диполя в двух случаях.
1. Напряженность поля на продолжении оси диполя в точке А (рис. 3). Используя принцип суперпозиции полей, имеем:
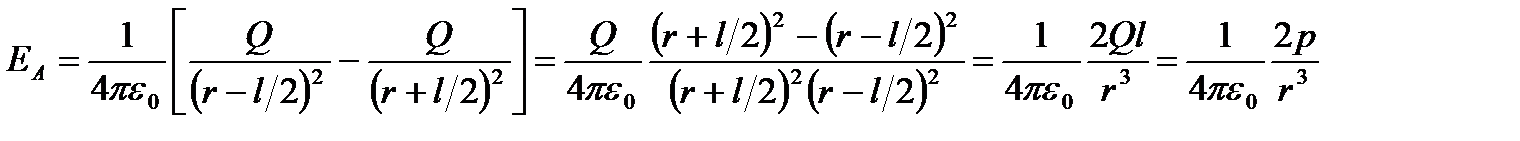 .
.
Здесь учитывается, что l/2<<r.
2. Напряженность поля на перпендикуляре, восстановленном к оси из его середины:
 .
.
Причем вектор Ев имеет направление, противоположное вектору электрического момента диполя.
Теорема Остроградского-Гаусса для электростатических полей в вакууме.
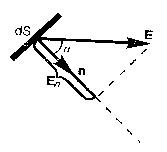 Рис. 4
Рис. 4
|
Вычисление напряженности поля системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно значительно упростить, используя теорему Гаусса, определяющую поток вектора напряженности электрического поля сквозь произвольную замкнутую поверхность.
Величина 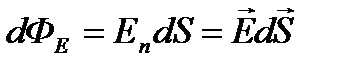 называется потоком вектора напряженности через площадку dS. Здесь dS=dSn – вектор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке;
называется потоком вектора напряженности через площадку dS. Здесь dS=dSn – вектор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке; 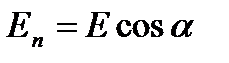 – проекция вектора Е на нормаль n к площадке dS (рис. 4).
– проекция вектора Е на нормаль n к площадке dS (рис. 4).
Итак, теорема Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0:
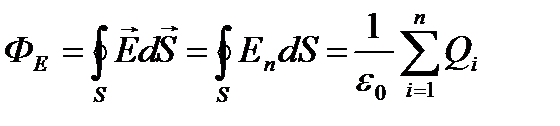 . (5)
. (5)
Рассмотрим несколько случаев применения теоремы Гаусса для расчета электростатических полей.
1. Поле равномерно заряженной бесконечной плоскости. Пусть бесконечная плоскость заряжена с постоянной поверхностной плотностью s, тогда напряженность создаваемого поля будет равна: 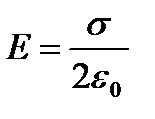 .
.
 Рис. 5
Рис. 5
|
2. Поле двух бесконечных параллельных разноименно заряженных плоскостей. Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями +s и -s. Тогда результирующее поле определится 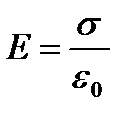 .
.
3. Поле равномерно заряженной сферической поверхности. Пусть сферическая поверхность радиуса R с общим зарядом Q заряжена равномерно с поверхностной плотностью +s. В таком случае напряженность поля будет равна: 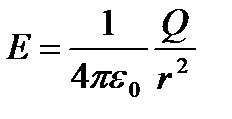 (
( 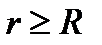 ). График зависимости напряженности поля Е заряженной сферической поверхности от расстояния r от ее центра приведен на рис. 5.
). График зависимости напряженности поля Е заряженной сферической поверхности от расстояния r от ее центра приведен на рис. 5.
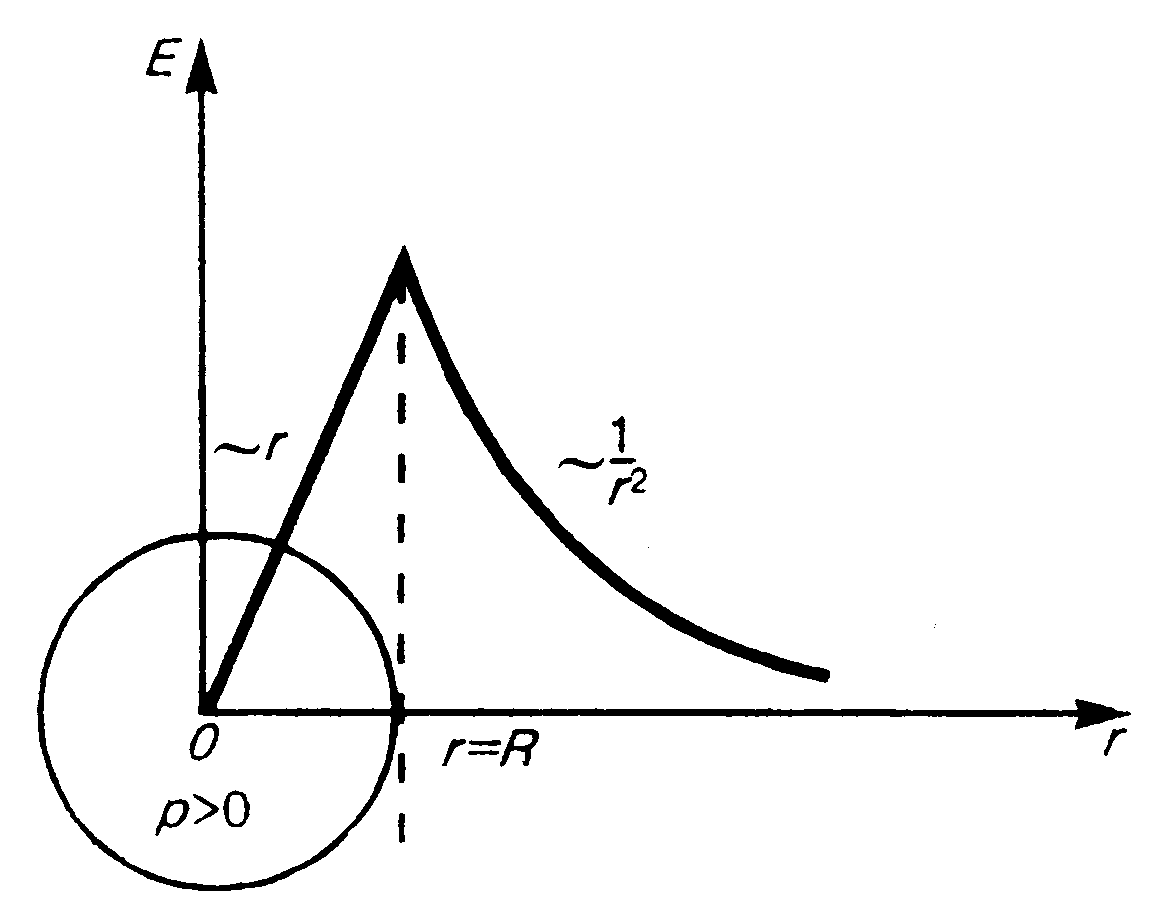 Рис. 6 Рис. 6
|
4. Поле объемно заряженного шара. Пусть шар радиуса R с общим зарядом Q заряжен равномерно с объемной плотностью r. Учитывая соображения симметрии, можно показать, что для напряженности поля вне шара получится тот же результат, что и в предыдущем случае. Внутри же шара напряженность поля будет другая: 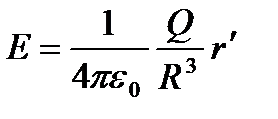 (
(  ). График зависимости Е от r для рассмотренного случая приведен на рис. 6.
). График зависимости Е от r для рассмотренного случая приведен на рис. 6.
5. Поле равномерно заряженного бесконечного цилиндра (нити). Пусть бесконечный цилиндр радиуса R заряжен равномерно с линейной плотностью t. В этом случае напряженность поля определится выражением:  (
( 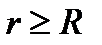 ). Внутри цилиндра (r<R) поле отсутствует.
). Внутри цилиндра (r<R) поле отсутствует.
Циркуляция вектора напряженности электростатического поля
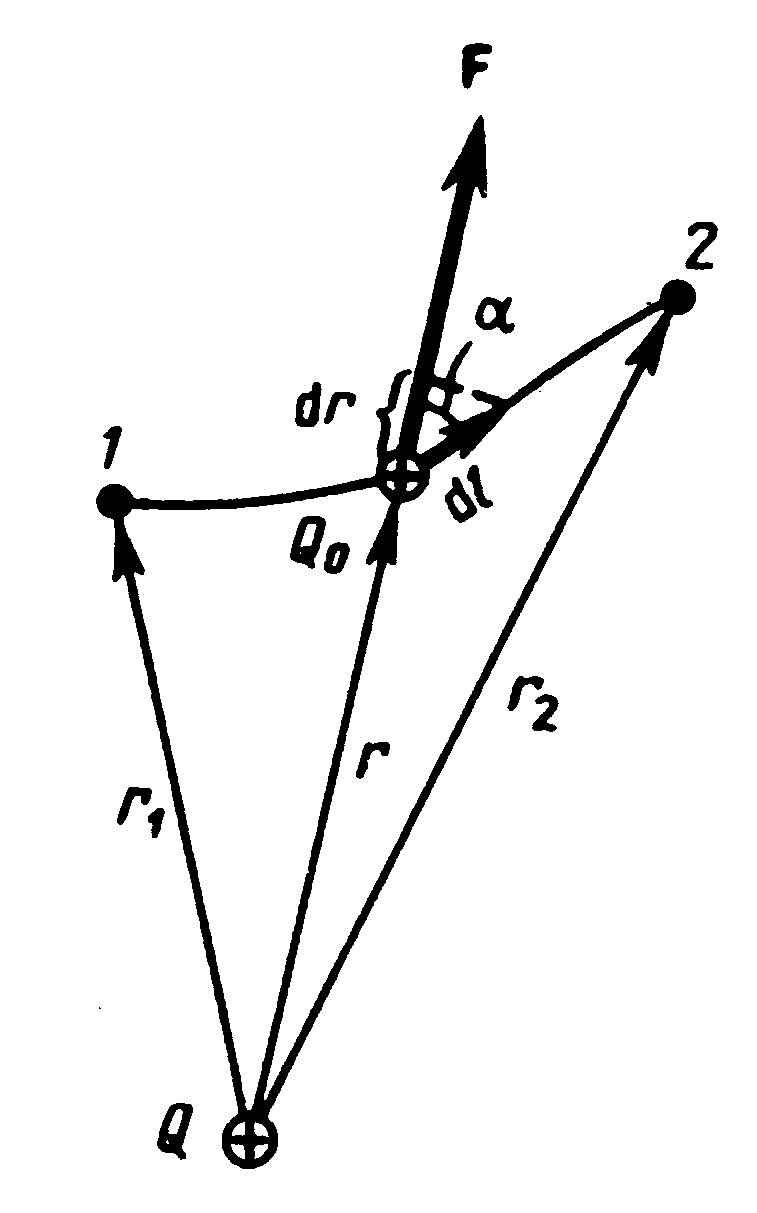 Рис. 7
Рис. 7
|
Если в электростатическом поле точечного заряда Q из точки 1 в точку 2 вдоль произвольной траектории (рис. 7) перемещается другой точечный заряд Q0, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна
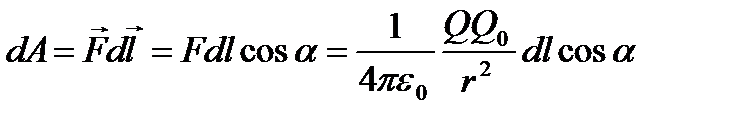 .
.
Так как 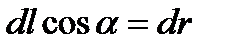 , то
, то
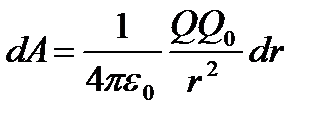 .
.
Работа при перемещении заряда Q0 из точки 1 в точку 2
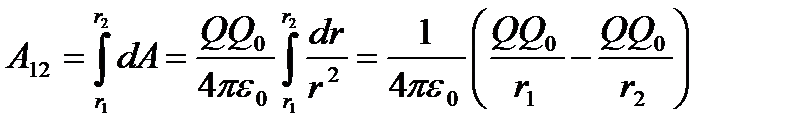 (6)
(6)
не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными.
Из формулы (6) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е.
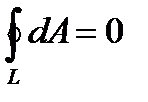 . (7)
. (7)
Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный положительный заряд, то элементарная работа сил поля на пути dl равна 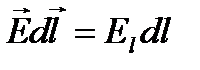 , где
, где 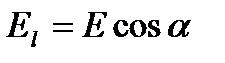 – проекция вектора Е на направление элементарного перемещения. Тогда формулу (7) можно записать в виде
– проекция вектора Е на направление элементарного перемещения. Тогда формулу (7) можно записать в виде
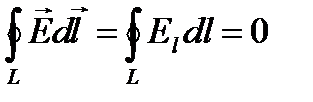 . (8)
. (8)
Интеграл называется циркуляцией вектора напряженности. Следовательно, циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю. Силовое поле, обладающее свойством (8), называется потенциальным. Из обращения в нуль циркуляции вектора Е следует, что линии напряженности электростатического поля не могут быть замкнутыми, они начинаются и кончаются на зарядах или же уходят в бесконечность. Формула (8) справедлива только для электростатического поля. В дальнейшем будет показано, что для поля движущихся зарядов условие (8) не выполняется.
Потенциал электростатического поля
Тело, находящееся в потенциальном поле сил, обладает потенциальной энергией, за счет которой силами поля совершается работа. Как известно, согласно закона сохранения энергии, работа консервативных сил совершается за счет убыли потенциальной энергии. Поэтому работу сил электростатического поля (6) можно представить как разность потенциальных энергий, которыми обладает точечный заряд Q0 в начальной и конечной точках поля заряда Q:
 .
.
Отсюда следует, что потенциальная энергия заряда Q0, находящегося в поле заряда Q на расстоянии r от него, равна
 . (9)
. (9)
Для одноименных зарядов Q0Q>0 и потенциальная энергия их взаимодействия (отталкивания) положительна, для разноименных зарядов Q0Q<0 и потенциальная энергия их взаимодействия (притяжения) отрицательна.
Если поле создается системой n точечных зарядов Q1, Q2, …, Qn, то работа электростатических сил, совершаемая над зарядом Q0, равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности. Поэтому потенциальная энергия W заряда Q0, находящегося в этом поле, определится:
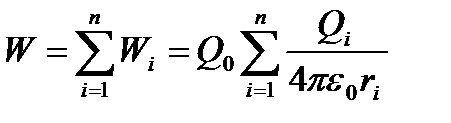 . (10)
. (10)
Из формул (9) и (10) вытекает, что отношение W/Q0 не зависит от Q0 и является поэтому энергетической характеристикой электростатического поля, называемой потенциалом:
 . (11)
. (11)
Итак, потенциал j в какой-либо точке электростатического поля есть физическая величина, определяемая потенциальной энергией единичного положительного заряда, помещенного в эту точку. Из формул (9) и (11) следует, что потенциал поля, создаваемого точечным зарядом Q, равен:
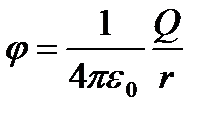 . (12)
. (12)
Работа, совершаемая силами электростатического поля при перемещении заряда Q0 из точки 1 в точку 2, может быть представлена как
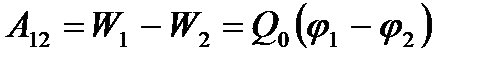 , (13)
, (13)
т.е. равна произведению перемещаемого заряда на разность потенциалов в начальной и конечной точках. Если перемещать заряд Q0 из произвольной точки за пределы поля, т.е. в бесконечность, где, по условию, потенциал равен нулю, то работа сил электростатического поля, согласно (13), 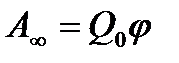 , откуда
, откуда
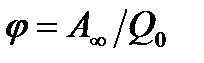 . (14)
. (14)
Таким образом, потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его в бесконечность. В системе СИ за единицу потенциала принят вольт (В).
Из формул (10) и (11) вытекает, что если поле создается несколькими зарядами, то потенциал поля системы зарядов равен алгебраической сумме потенциалов полей всех этих зарядов: 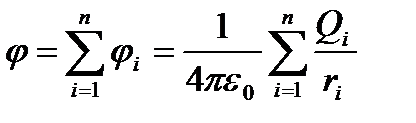 .
.
Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом – энергетической характеристикой поля. Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и x1-x2=dx, равна Exdx. Та же работа равна j1-j2=dj. Приравняв оба выражения, можем записать
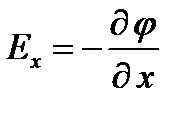 .
.
Повторив аналогичные рассуждения для осей y и z, можем найти вектор Е:
 ,
,
где i, j, k – единичные векторы координатных осей x, y, z. Используя определение градиента, последнее выражение можно переписать в виде:
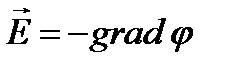 , (15)
, (15)
т.е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
Для графического изображения распределения потенциала электростатического поля пользуются эквипотенциальными поверхностями – поверхностями, во всех точках которых потенциал j имеет одно и то же значение. Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т.е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Е всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим поверхностям.
6. Классификация диэлектриков и их поляризация
Напомним, что диэлектрики – это тела, в которых практически отсутствуют свободные заряды. В электростатике принимается, что диэлектрики состоят из диполей. По их виду эти вещества делят на три группы.
Первую группу диэлектриков (азот, водород, углекислый газ, кислород и т.п.) составляют вещества, молекулы которых имеют симметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов в отсутствие внешнего электрического поля совпадают и, следовательно, дипольный момент молекулы р равен нулю. Молекулы таких диэлектриков называют неполярными. Под действием внешнего электрического поля заряды неполярных молекул смещаются в противоположные стороны (положительные по полю, отрицательные против поля) и молекула приобретает дипольный момент.
Вторую группу диэлектриков (вода, аммиак, большинство оксидов) составляют вещества, молекулы которых имеют асимметричное строение, т.е. центры «тяжести» положительных и отрицательных зарядов не совпадают. Таким образом, эти молекулы в отсутствие внешнего электрического поля обладают дипольным моментом. Молекулы таких диэлектриков называются полярными. При отсутствии внешнего поля, однако, дипольные моменты полярных молекул вследствие теплового движения ориентированы в пространстве хаотично и их результирующий момент равен нулю. Если такой диэлектрик поместить во внешнее поле, то силы этого поля будут стремиться повернуть диполи вдоль поля и возникает отличный от нуля результирующий момент.
Третью группу диэлектриков (NaCl, KCl, KBr, …) составляют вещества, молекулы которых имеют ионное строение. Ионные кристаллы представляют собой пространственные решетки с правильным чередованием ионов разных знаков. В этих кристаллах нельзя выделить отдельные молекулы, а рассматривать их можно как систему двух вдвинутых одна в другую ионных подрешеток. При наложении на ионный кристалл электрического поля происходит некоторая деформация кристаллической решетки или относительное смещение подрешеток, приводящее к возникновению дипольных моментов.
Таким образом, внесение всех трех групп диэлектриков во внешнее электрическое поле приводит к возникновению отличного от нуля результирующего момента диэлектрика, или, иными словами, к поляризации диэлектрика. Поляризацией диэлектрика называется процесс ориентации диполей или появления под действием внешнего электрического поля ориентированных по полю диполей. Соответственно трем группам диэлектриков различают три вида поляризации:
- электронная, или деформационная, поляризация диэлектрика с неполярными молекулами, заключающаяся в возникновении у атомов индуцированного дипольного момента за счет деформации электронных орбит;
- ориентационная, или дипольная, поляризация диэлектрика с полярными молекулами, заключающаяся в ориентации имеющихся дипольных моментов молекул по полю. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрическое поле и тепловое движение)возникает преимущественная ориентация дипольных моментов молекул по полю. Эта ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура;
- ионная поляризация диэлектриков с ионными кристаллическими решетками, заключающаяся в смещении подрешетки положительных ионов вдоль поля, а отрицательных – против поля, приводящем к возникновению дипольных моментов.
Поляризованность. Электрическое смещение
Для количественного описания поляризации диэлектрика пользуются векторной величиной – поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:
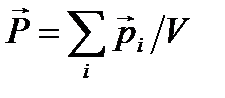 ,
,
где pi – дипольный момент одной молекулы. Из опыта следует, что для большого класса диэлектриков поляризованность Р линейно зависит от напряженности поля Е. Если диэлектрик изотропный и Е не слишком велико, то
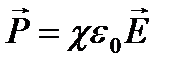 ,
,
где c - диэлектрическая восприимчивость вещества, характеризующая свойства диэлектрика.
Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электрическое поле Е0 пластинку из однородного диэлектрика. Внешнее поле Е0 создается, так называемыми, свободными зарядами. Под действием этого поля диэлектрик поляризуется, т.е. происходит смещение зарядов: положительные смещаются по полю, отрицательные – против поля. В результате этого на одной грани диэлектрика, обращенной к отрицательному полюсу, будет избыток положительного заряда, а на другой – отрицательного заряда. Эти нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Итак, поле внутри диэлектрика направлено в противоположную сторону внешнему полю, т.е. поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е=Е0. Напряженность результирующего поля внутри диэлектрика равна
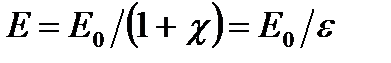 , (16)
, (16)
где величина e=1+c называется диэлектрической проницаемостью среды. Видно, что e показывает, во сколько раз поле ослабляется диэлектриком, и характеризует количественно свойство диэлектрика поляризоваться в электрическом поле.
Из (16) следует, что вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен
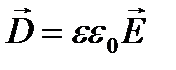 . (17)
. (17)
Или 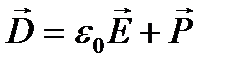 . Единица электрического смещения – кулон на метр в квадрате (Кл/м2).
. Единица электрического смещения – кулон на метр в квадрате (Кл/м2).
Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Связанные заряды, возникающие в диэлектрике, могут вызвать, однако, перераспределение свободных зарядов, создающих поле. Поэтому вектор D характеризует электростатическое поле, создаваемое свободными зарядами (т.е. в вакууме), но при таком их распределении в пространстве, какое имеется при наличии диэлектрика.
Аналогично, как и поле Е, поле D изображается с помощью линий электрического смещения, направление и густота которых определяются точно так же, как и для линий напряженности. Линии вектора Е могут начинаться и заканчиваться на любых зарядах – свободных и связанных, в то время как линии вектора D – только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.
Теорема Гауссы для электростатического поля в диэлектрике:
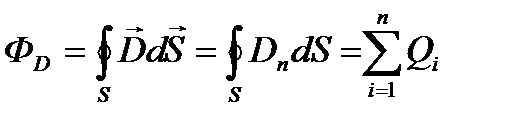 , (18)
, (18)
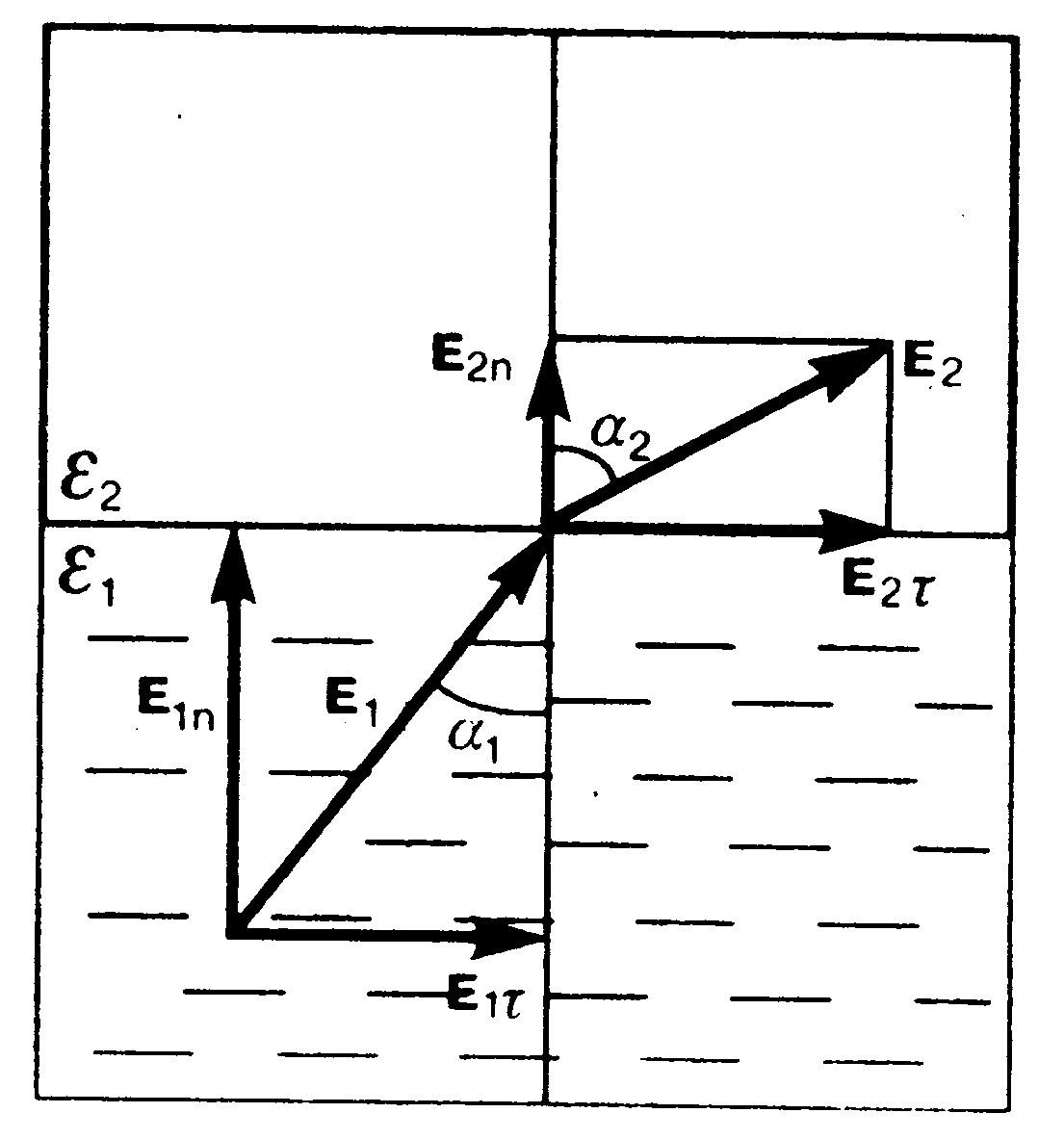 Рис. 8
Рис. 8
|
т.е. поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов.
Интересен случай распространения электростатического поля на границе двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e1 и e2) при отсутствии на границе свободных зарядов (рис. 8). При переходе через границу раздела двух диэлектрических сред линии векторов Е и D испытывают излом, который подчиняется следующей закономерности:
 .
.
Эта формула показывает, что, входя в диэлектрик с большей диэлектрической проницаемостью, линии E и D удаляются от нормали.
Сегнетоэлектрики, пьезоэлектрики, проводники в электростатическом поле
Сегнетоэлектрики – диэлектрики, обладающие в определенном интервале температур спонтанной (самопроизвольной) поляризованностью, т.е. поляризованностью в отсутствие внешнего электрического поля.
При отсутствии внешнего электрического поля сегнетоэлектрик представляет собой как бы мозаику из доменов – областей с различными направлениями поляризованности. Так как в смежных доменах эти направления различны, то в целом дипольный момент диэлектрика равен нулю. При внесении сегнетоэлектрика во внешнее поле происходит переориентация дипольных моментов по полю, а возникшее при этом суммарное электрическое поле доменов будет поддерживать их некоторую определенную ориентацию и после прекращения действия внешнего поля. Поэтому сегнетоэлектрики имеют аномально большие значения диэлектрической проницаемости (до 104). Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сегнетоэлектрика имеется определенная температура, выше которой его необычные свойства исчезают и он становится обычным диэлектриком. Эта температура называется точкой Кюри. Диэлектрическая проницаемость e сегнетоэлектриков зависит от напряженности Е поля в веществе, а для других диэлектриков эти величины являются характеристиками вещества.
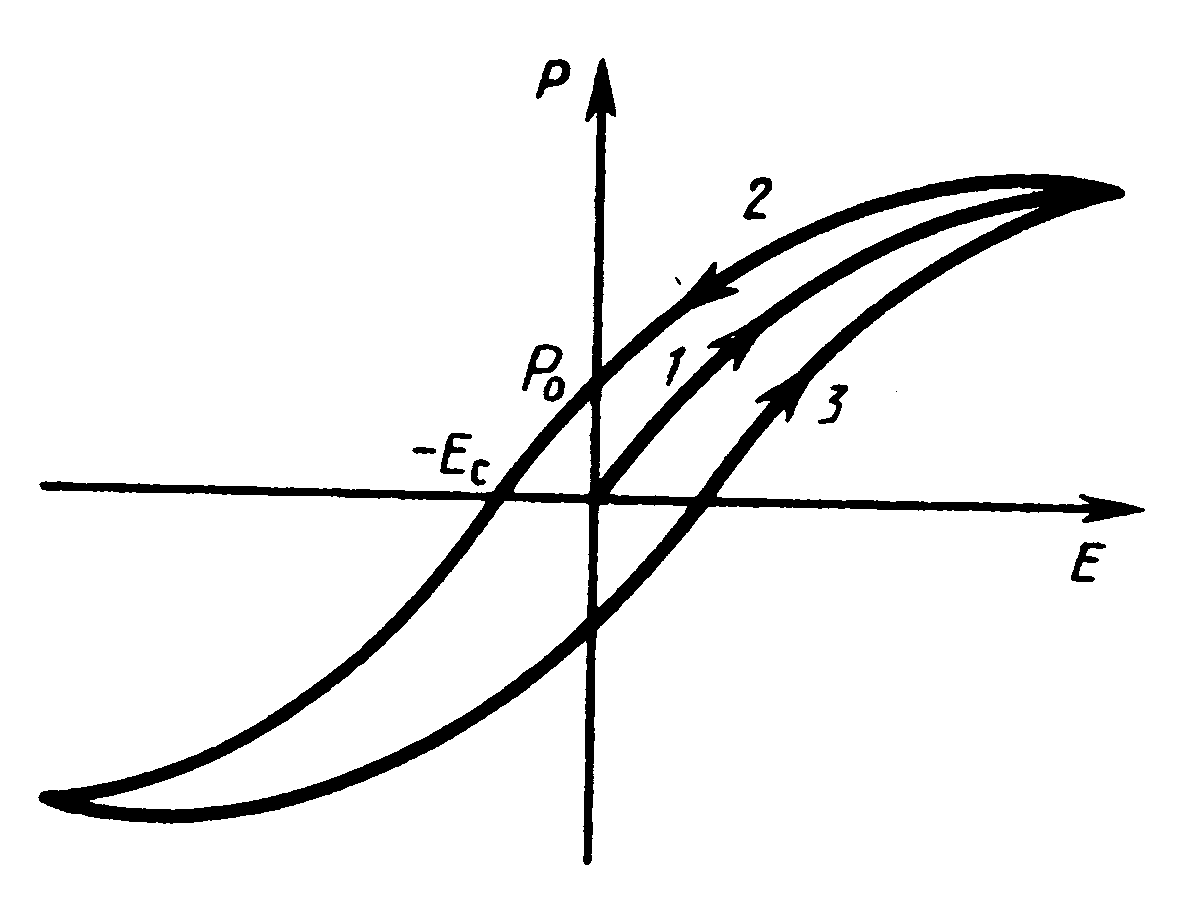 Рис. 9
Рис. 9
|
Для сегнетоэлектриков формула  не соблюдается; для них связь между вектором поляризованности Р и напряженности Е нелинейная и зависит от значений Е в предшествующие моменты времени. В сегнетоэлектриках наблюдается явление диэлектрического гистерезиса («запаздывания»). Как видно из рис. 9, с увеличением напряженности Е внешнего электрического поля поляризованность Р растет, достигая насыщения (кривая 1). Уменьшение Р с уменьшением Е происходит по кривой 2, и при Е=0 сегнетоэлектрик сохраняет остаточную поляризованность Р0, т.е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля. Чтобы уничтожить остаточную поляризованность, надо приложить электрическое поле обратного направления (-Ес). Величина Ес называется коэрцитивной силой. Если далее Е изменять, то Р изменяется по кривой 3 петли гистерезиса.
не соблюдается; для них связь между вектором поляризованности Р и напряженности Е нелинейная и зависит от значений Е в предшествующие моменты времени. В сегнетоэлектриках наблюдается явление диэлектрического гистерезиса («запаздывания»). Как видно из рис. 9, с увеличением напряженности Е внешнего электрического поля поляризованность Р растет, достигая насыщения (кривая 1). Уменьшение Р с уменьшением Е происходит по кривой 2, и при Е=0 сегнетоэлектрик сохраняет остаточную поляризованность Р0, т.е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля. Чтобы уничтожить остаточную поляризованность, надо приложить электрическое поле обратного направления (-Ес). Величина Ес называется коэрцитивной силой. Если далее Е изменять, то Р изменяется по кривой 3 петли гистерезиса.
Следует упомянуть еще о пьезоэлектриках – кристаллических веществах, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация даже в отсутствие внешнего электрического поля (прямой пьезоэффект). Наблюдается и обратный пьезоэффект – появление механической деформации под действием электрического поля.
Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю: Е=0.
Так как в состоянии равновесия внутри проводника заряды отсутствуют, то создание внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Следовательно, внутри полости поле будет отсутствовать. Если теперь этот проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т.е. полость полностью изолирована от влияния внешних электростатических полей. На этом основана электростатическая защита – экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Вместо сплошного проводника для защиты может быть использована густая металлическая сетка, которая, кстати, является эффективной при наличии не только постоянных, но и переменных электрических полей.
Электроемкость. Конденсаторы. Энергия электрического поля.
Рассмотрим уединенный проводник, т.е. проводник, который удален от других проводников, тел и зарядов. Его потенциал, согласно (12), прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, имеют разные потенциалы. Поэтому для уединенного проводника можно записать 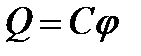 .
.
Величину
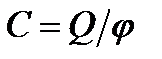 (19)
(19)
называют электроемкостью (или просто емкостью) уединенного проводника. Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость проводника зависит только от его размеров и формы. Например, емкость шара радиуса R определяется по формуле
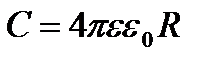 .
.
Единица электроемкости – фарад (Ф). Фарад – очень большая величина, поэтому на практике используются дольные единицы – миллифарад (мФ), микрофарад (мкФ) и т.д..
Конденсаторами называют устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладающие большой емкостью. Обычный конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. В зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические. Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, возникающие на разных обкладках, являются равными по модулю разноименными зарядами. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j1-j2) между его обкладками:
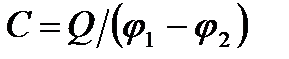 . (20)
. (20)
Чаще всего на практике используются плоские конденсаторы, емкость которых рассчитывают по формуле:
 ,
,
где S – площадь одной обкладки, d – расстояние между ними, e - диэлектрическая проницаемость вещества, заполняющего пространство между обкладками.
Конденсаторы характеризуются пробивным напряжением – разностью потенциалов между обкладками конденсатора, при которой происходит пробой – электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.
Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединения.
а) 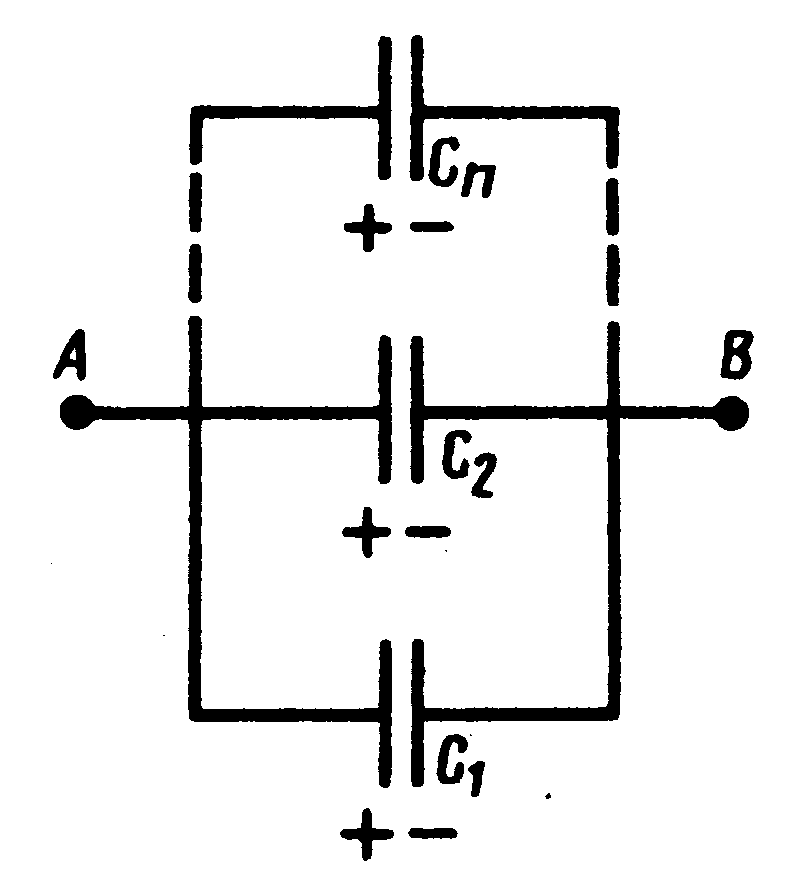 б)
б)  Рис. 10
Рис. 10
|
1. Параллельное соединение конденсаторов (рис. 10, а). У параллельно соединенных конденсаторов разность потенциалов на обкладках одинакова и равна (jА - jВ). Заряд батареи конденсаторов
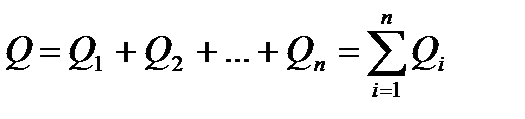 .
.
Полная емкость батареи
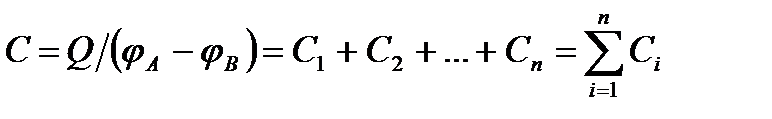 ,
,
т.е. при параллельном соединении конденсаторов она равна сумме емкостей отдельных конденсаторов.
2. Последовательное соединение конденсаторов (рис. 10, б). В этом случае заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи
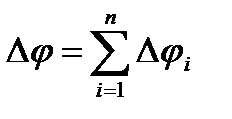 .
.
При последовательном соединении конденсаторов для вычисления полной емкости батареи суммируются величины, обратные емкостям:
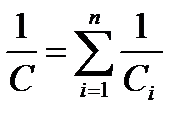 .
.
Электростатические силы взаимодействия консервативны, следовательно, система зарядов обладает потенциальной энергией. В случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна
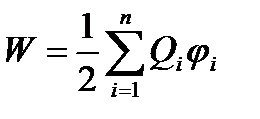 , (21)
, (21)
где ji – потенциал, создаваемый в той точку, где находится заряд Qi, всеми зарядами, кроме i-го.
Энергию любого заряженного проводника, а значит, и любого заряженного конденсатора можно определить по формуле:
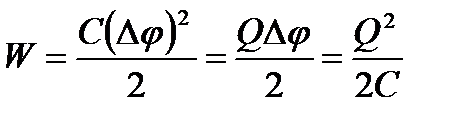 . (22)
. (22)
Преобразуем формулу (22) для случая плоского конденсатора, воспользовавшись выражением для емкости ( 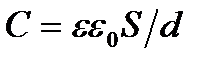 ) и разности потенциалов между его обкладками (
) и разности потенциалов между его обкладками (  ). Тогда
). Тогда
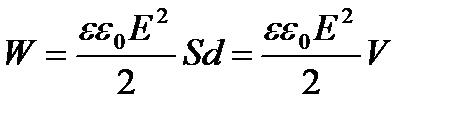 ,
,
где V=Sd – объем конденсатора.
Объемная плотность энергии электростатического поля (энергия единицы объема)
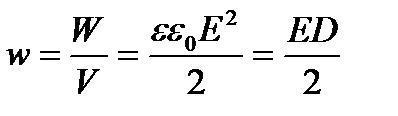 . (23)
. (23)
Это выражение справедливо только для изотропного диэлектрика, для которого выполняется соотношение 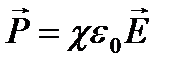 .
.
Лекция 2
Электродинамика.
Электрический ток, сила тока и плотность тока, ЭДС и напряжение
Электродинамика – раздел учения об электричестве, в котором рассматриваются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел. Электрическим током называется любое упорядоченное (направленное) движение электрических зарядов. В проводнике под действием приложенного электрического поля Е свободные электрические заряды перемещаются: положительные – по полю, отрицательные – против поля, т.е. в проводнике возникает электрический ток, называемый током проводимости. Если же упорядоченное движение электрических зарядов осуществляется перемещением в пространстве заряженного макроскопического тела, то возникает так называемый конвекционный ток.
Для возникновения и существования электрического тока необходимо, с одной стороны, наличие свободных носителей тока – заряженных частиц, способных перемещаться упорядоченно, а с другой – наличие электрического поля, энергия которого, каким-то образом восполняясь, расходовалась бы на их упорядоченное движение. За направление тока условно принимают направление движения положительных зарядов.
Количественной мерой электрического тока служит сила тока I – скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени:
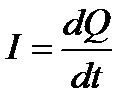 . (24)
. (24)
Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным. Единица силы тока – ампер (А).
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока:
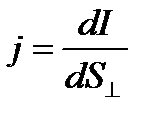 . (25)
. (25)
Если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е, причем эти заряды движутся упорядоченно со средней скоростью <v>, то плотность тока можно выразить как
 .
.
Плотность тока – вектор, ориентированный по направлению тока, т.е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов. Единица плотности тока – ампер на метр в квадрате (А/м2).
Для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Природа сторонних сил может быть различной.
Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС), действующей в цепи:
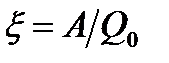 .
.
ЭДС, как и потенциал, выражается в вольтах.
Напряжением U на участке 1-2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке:
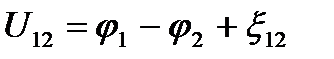 .
.
Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т.е. сторонние силы отсутствуют.
Законы Ома. Сопротивление проводников
Немецкий физик Г. Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т.е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:
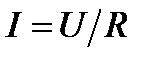 , (26)
, (26)
где R – электрическое сопротивление проводника. Уравнение (26) выражает закон Ома для однородного участка цепи. За единицу сопротивления принят 1 Ом.
Величина
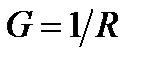
называется электрической проводимостью проводника. Единица проводимости – сименс (См).
Сопротивление проводников зависит от размеров и формы, а также от материала, из которого проводник изготовлен. Так для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S:
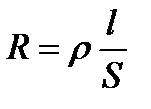 ,
,
где r - коэффициент пропорциональности, характеризующий материал проводника и называемый удельным электрическим сопротивлением.
Подставив последнее выражение в формулу (26), получим
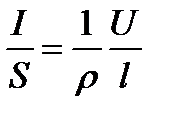 ,
,
где величина, обратная удельному сопротивлению, g=1/r называется удельной электрической проводимостью вещества проводника. Учитывая, что 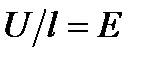 – напряженность электрического поля в проводнике,
– напряженность электрического поля в проводнике, 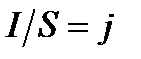 – плотность тока, можно записать
– плотность тока, можно записать 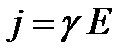 . Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому последнее выражение записывают в виде:
. Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е, то направления j и Е совпадают. Поэтому последнее выражение записывают в виде:
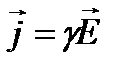 , (27)
, (27)
и называют законом Ома в дифференциальной форме.
Опыт показывает, что в первом приближении изменение удельного сопротивления, а значит и сопротивления, с температурой описывается линейным законом:
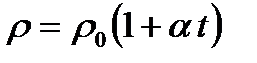 ,
, 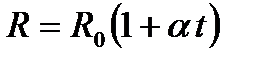 ,
,
где r и r0, R и R0 – соответственно удельные сопротивления и сопротивления проводника при t и 0 °С, a - температурный коэффициент сопротивления, для чистых металлов (при не очень низких температурах) близкий к 1/273 К-1.
Теперь рассмотрим неоднородный участок цепи, где действующую ЭДС на участке 1-2 обозначим через 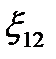 , а приложенную на концах участка разность потенциалов – через
, а приложенную на концах участка разность потенциалов – через 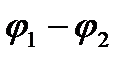 . Используя понятие напряжения и формулу (26), можно получить закон Ома для неоднородного участка цепи в интегральной форме:
. Используя понятие напряжения и формулу (26), можно получить закон Ома для неоднородного участка цепи в интегральной форме:
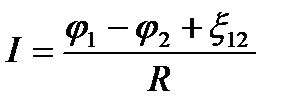 , (28)
, (28)
который является обобщенным законом Ома. Если на данном участке цепи источник тока отсутствует ( 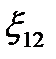 =0), то из (28) приходим к закону Ома для однородного участка цепи (26). Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, т.е.
=0), то из (28) приходим к закону Ома для однородного участка цепи (26). Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, т.е. 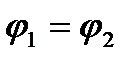 ; тогда из (28) получаем закон Ома для замкнутой цепи:
; тогда из (28) получаем закон Ома для замкнутой цепи:
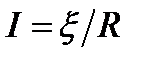 ,
,
где x - ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи. В общем случае  , где r – внутренне сопротивление источника тока, R1 – сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид:
, где r – внутренне сопротивление источника тока, R1 – сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид:
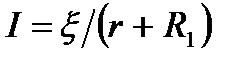 . (29)
. (29)
Закон Джоуля-Ленца. Правила Кирхгофа.
Рассмотрим однородный проводник, к концам которого приложено напряжение U. За время dt через сечение проводника переносится заряд dq=Idt. Так как ток представляет собой перемещение заряда под действием электрического поля, то, по формуле (13), работа тока
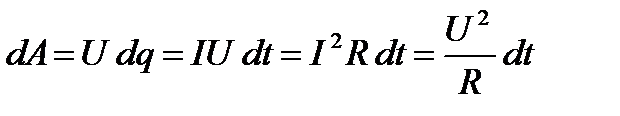 . (30)
. (30)
По определению мощности и с использованием формулы (30) можно получить выражение для мощности тока:
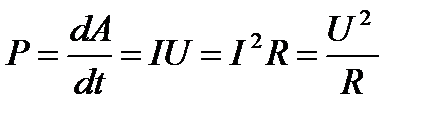 . (31)
. (31)
Работа тока выражается в джоулях, а мощность – в ваттах. На практике применяются также внесистемные единицы работы тока: ватт-час (Вт×ч) и киловатт-час (кВт×ч). 1 Вт×ч – работа тока мощностью 1 Вт в течение 1 ч, т.е. 1 Вт×ч=3600 Вт×с=3,6×103 Дж.
Если ток проходит по неподвижному металлическому проводнику, то вся работа тока идет на его нагревание и, по закону сохранения энергии,  . Таким образом, используя выражение (30), получим
. Таким образом, используя выражение (30), получим
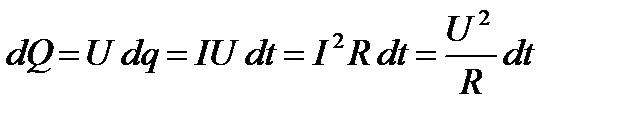 . (32)
. (32)
Это выражение представляет собой закон Джоуля-Ленца.
Выделим в проводнике элементарный цилиндрический объем 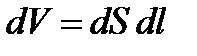 (ось цилиндра совпадает с направлением тока), сопротивление которого
(ось цилиндра совпадает с направлением тока), сопротивление которого 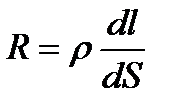 . По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота
. По закону Джоуля-Ленца, за время dt в этом объеме выделится теплота
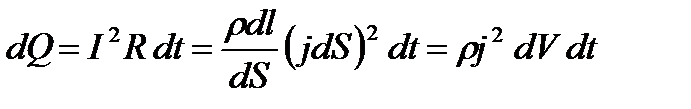 .
.
Количество теплоты, выделяющееся за единицу времени в единице объема, называется удельной тепловой мощностью тока:
 . (33, а)
. (33, а)
Используя дифференциальную форму закона Ома ( 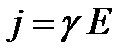 ) и соотношение r=1/g, получим
) и соотношение r=1/g, получим
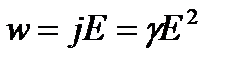 . (33, б)
. (33, б)
Формулы (33) являются обобщенным выражением закона Джоуля-Ленца в дифференциальной форме, пригодным для любого проводника.
Обобщенный закон Ома (28) позволяет рассчитать практически любую сложную цепь. Однако непосредственный расчет разветвленных цепей, содержащих несколько замкнутых контуров, довольно сложен. Эта задача решается более просто с помощью двух правил Кирхгофа.
Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, – отрицательным.
Итак, первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю
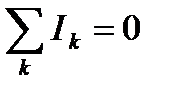 .
.
Второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Ii на сопротивления Ri соответствующих участков этого контура равна алгебраической сумме ЭДС xk, встречающихся в этом контуре
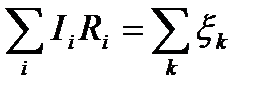 .
.
Эмиссионные явления. Электрический ток в газах. Плазма.
Как известно, для существования электрического тока необходимо наличие свободных электронов. Как показывает опыт, свободные электроны при обычных температурах практически не покидают металл. Следовательно, в поверхностном слое металла должно быть задерживающее электрическое поле, препятствующее выходу электронов из металла в окружающий вакуум. Работа, которую нужно затратить для удаления электрона из металла в вакуум, называется работой выхода. Работа выхода выражается в электрон-вольтах (эВ): 1 эВ равен работе, совершаемой силами поля при перемещении элементарного электрического заряда при прохождении им разности потенциалов в 1 В. Так как заряд электрона равен 1,6×10-19 Кл, то 1 эВ=1,6×10-19 Дж. Работа выхода зависит от химической природы металлов и от чистоты их поверхности и колеблется в пределах нескольких электрон-вольт.
Если сообщить электронам в металлах энергию, необходимую для преодоления работы выхода, то часть электронов может покинуть металл, в результате чего наблюдается явление испускания электронов, или электронной эмиссии. В зависимости от способа сообщения электронам энергии различают четыре вида эмиссии.
1. Термоэлектронная эмиссия – это испускание электронов нагретыми металлами. Концентрация свободных электронов в металлах достаточно высока, поэтому доже при средних температурах вследствие распределения электронов по скоростям (по энергиям) некоторые электроны обладают энергией, достаточной для преодоления потенциального барьера на границе металла. С повышением температуры число электронов, кинетическая энергия теплового движения которых больше работы выхода, растет и явление термоэлектронной эмиссии становится заметным.
2. Фотоэлектронная эмиссия – это эмиссия электронов из металла под действием света, а также коротковолнового электромагнитного излучения (например, рентгеновского).
3. Вторичная электронная эмиссия – это испускание электронов поверхностью металлов, полупроводников или диэлектриков при бомбардировке их пучком электронов. Вторичный электронный поток состоит из электронов, отраженных поверхностью (упруго и неупруго отраженные электроны), и «истинно» вторичных электронов – электронов, выбитых из металла, полупроводника или диэлектрика первичными электронами.
4. Автоэлектронная эмиссия – это эмиссия электронов с поверхности металлов под действием сильного внешнего электрического поля.
Газы при не слишком высоких температурах и при давлениях, близких к атмосферному, являются хорошими изоляторами. Это объясняется тем, что газы при обычных условиях состоят из нейтральных атомов и молекул и не содержат свободных зарядов (электронов и ионов). Газ становится проводником электричества, когда некоторая часть его молекул ионизируется, т.е. произойдет расщепление нейтральных атомов и молекул на ионы и свободные электроны. Для этого газ надо подвергнуть действию какого-либо ионизатора. В ионизированном газе имеются положительные и отрицательные ионы и свободные электроны. Одновременно с процессом ионизации газа всегда идет и обратный процесс – процесс рекомбинации: положительные и отрицательные ионы, положительные ионы и электроны, встречаясь, воссоединяются между собой с образованием нейтральных атомов и молекул. Чем больше ионов возникает под действием ионизатора, тем интенсивнее идет и процесс рекомбинации.
Прохождение электрического тока через газы называются газовым разрядом. Разряды, существующие только под действием внешних ионизаторов, называются несамостоятельными. Разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным. В зависимости от давления газа, конфигурации электродов, параметров внешней цепи говорят о четырех типах самостоятельного разряда.
1. Тлеющий разряд возникает при низких давлениях. Характеризуется неодинаковыми по интенсивности излучения участками разряда. Используется в лампах дневного света, газосветных трубках для светящихся надписей и реклам.
2. Искровой разряд возникает при больших напряженностях электрического поля в газе, находящемся под давлением порядка атмосферного. Искра имеет вид ярко светящегося тонкого канала, сложным образом изогнутого и разветвленного (молния и т.п.).
3. Если после зажигания искрового разряда от мощного источника постепенно уменьшать расстояние между электродами, то разряд становится непрерывным – возникает дуговой разряд. При этом сила тока резко возрастает, достигая сотен ампер, а напряжение на разрядном промежутке падает до нескольких десятков вольт. Дуговой разряд находит применение для сварки и резки металлов.
4. Коронный разряд – высоковольтный электрический разряд при высоком (например, атмосферном) давлении в резко неоднородном поле вблизи электродов с большой кривизной поверхности (например, острия). Когда напряженность поля вблизи острия достигает 30 кВ/см, то вокруг него возникает свечение в виде короны, чем и вызвано название этого вида разряда.
Плазмой называется сильно ионизированный газ, в котором концентрации положительных и отрицательных зарядов практически одинаковы. Различают высокотемпературную плазму, возникающую при сверхвысоких температурах, и газоразрядную плазму, возникающую при газовом разряде. Плазма характеризуется степенью ионизации a – отношением числа ионизированных частиц к полному их числу в единице объема плазмы. В зависимости от величины a говорят о слабо (a составляет доли процента), умеренно (a – несколько процентов) и полностью (a близко к 100%) ионизированной плазме.
Плазма обладает следующими основными свойствами:
- высокой степенью ионизации газа, в пределе – полной ионизацией;
- равенством нулю результирующего пространственного заряда (концентрация положительных и отрицательных частиц в плазме практически одинакова);
- большой электропроводностью, причем ток в плазме создается в основном электронами, как наиболее подвижными частицами; свечением;
- сильным взаимодействием с электрическим и магнитным полями;
- колебаниями электронов в плазме с большой частотой (» 108 Гц), вызывающими общее вибрационное состояние плазмы;
- «коллективным» - одновременным взаимодействием громадного числа частиц (в обычных газах частицы взаимодействуют друг с другом попарно).
Эти свойства определяют качественное своеобразие плазмы, позволяющее считать ее особым, четвертым, состоянием вещества.
Лекция 3.
Дата добавления: 2015-12-16; просмотров: 2178;
