Магнитное поле и его характеристики. Движение заряженных частиц в электрических и магнитных полях.

Магнитное поле и его характеристики. Закон Био-Савара-Лапласа.

Опыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды.

Количественной характеристикой магнитного поля является вектор магнитной индукции В. Он является также силовой характеристикой и численно равен максимальному вращающему моменту, действующему на рамку с магнитным моментом, равным единице. В качестве единицы измерения магнитной индукции в системе СИ принимают тесла (Тл).

Так как магнитное поле является силовым, т.е. способно оказывать воздействие на что-либо, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции. Линии магнитной индукции всегда замкнуты и охватывают проводники с током.

В любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микротоки создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:

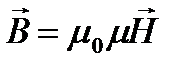, (1)

где m₀ – магнитная постоянная (m₀=4p×10^-7 Гн/м), m - безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды. В СИ напряженность магнитного поля измеряют в ампер на метр (А/м).

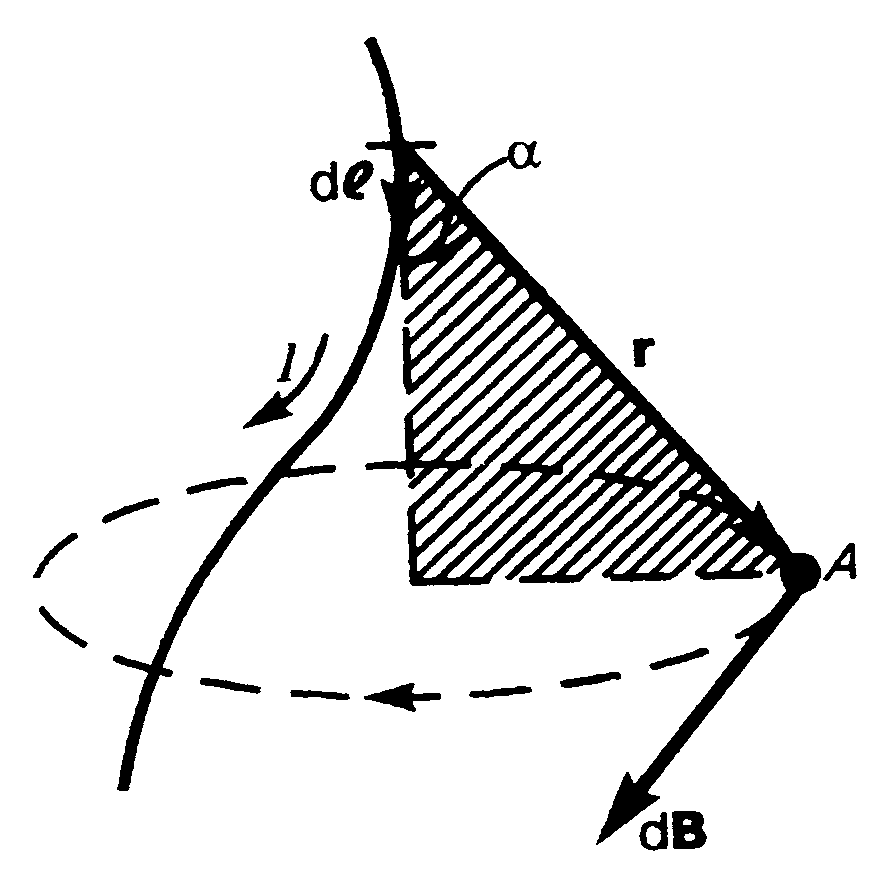Рис. 1

Закон Био-Савара-Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А (рис. 1) индукцию поля dB, записывается в виде

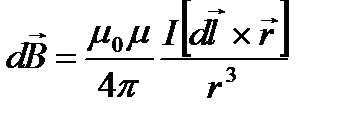, (2)

где dl – вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током, r – радиус-вектор, проведенный из элемента dl проводника в точку А поля, r – модуль радиуса-вектора r. Направление dB перпендикулярно dl и r, т.е. перпендикулярно плоскости, в которой они лежат, и совпадает с касательной к линии магнитной индукции. Это направление может быть найдено по правилу правого винта. Модуль вектора dB определяется выражением

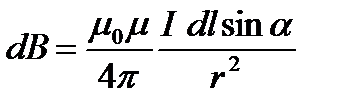, (3)

где a - угол между векторами dl и r.

Для магнитного поля справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемая несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

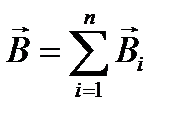. (4)

Рассмотрим применение закона Био-Савара-Лапласа к конкретным конфигурациям тока.

1. Магнитная индукция поля прямого тока – тока, текущего по тонкому прямому проводу бесконечной длины (рис. 2):

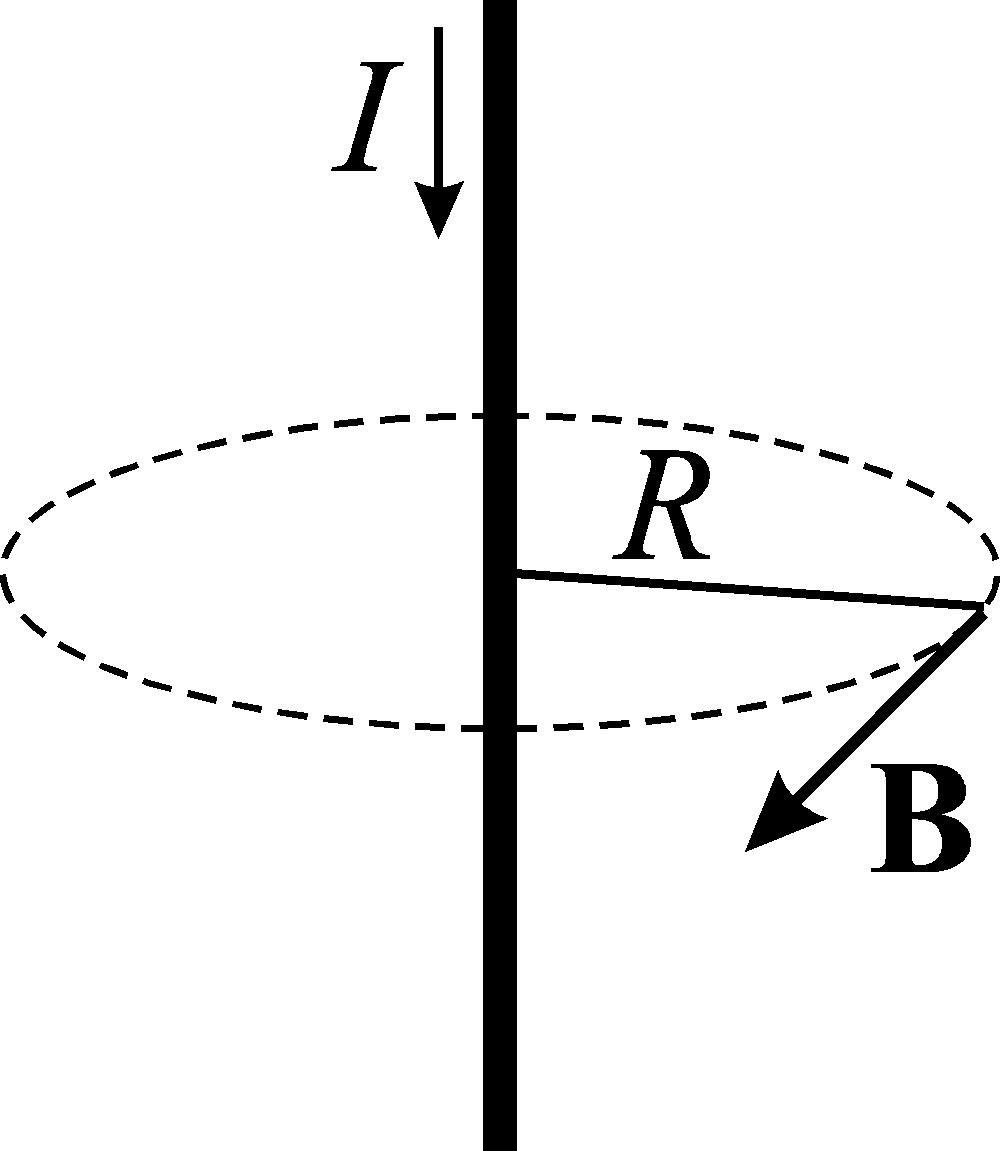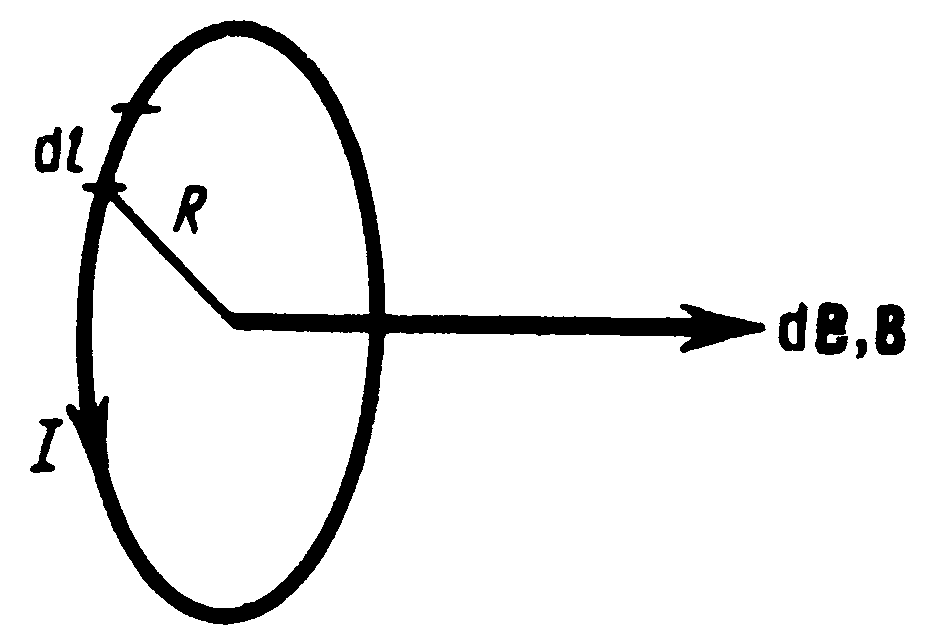Рис. 2 Рис.3

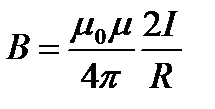, (5)

где R – расстояние от тока до искомой точки.

2. Магнитная индукция поля в центре кругового проводника с током (рис. 3):

, (6)

где R – радиус витка.

2. Закон Ампера. Магнитное поле движущегося заряда. Поток магнитной индукции.

Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила dF, с которой магнитное поле действует на элемент проводника dl с током, находящимся в магнитном поле, равна

, (7)

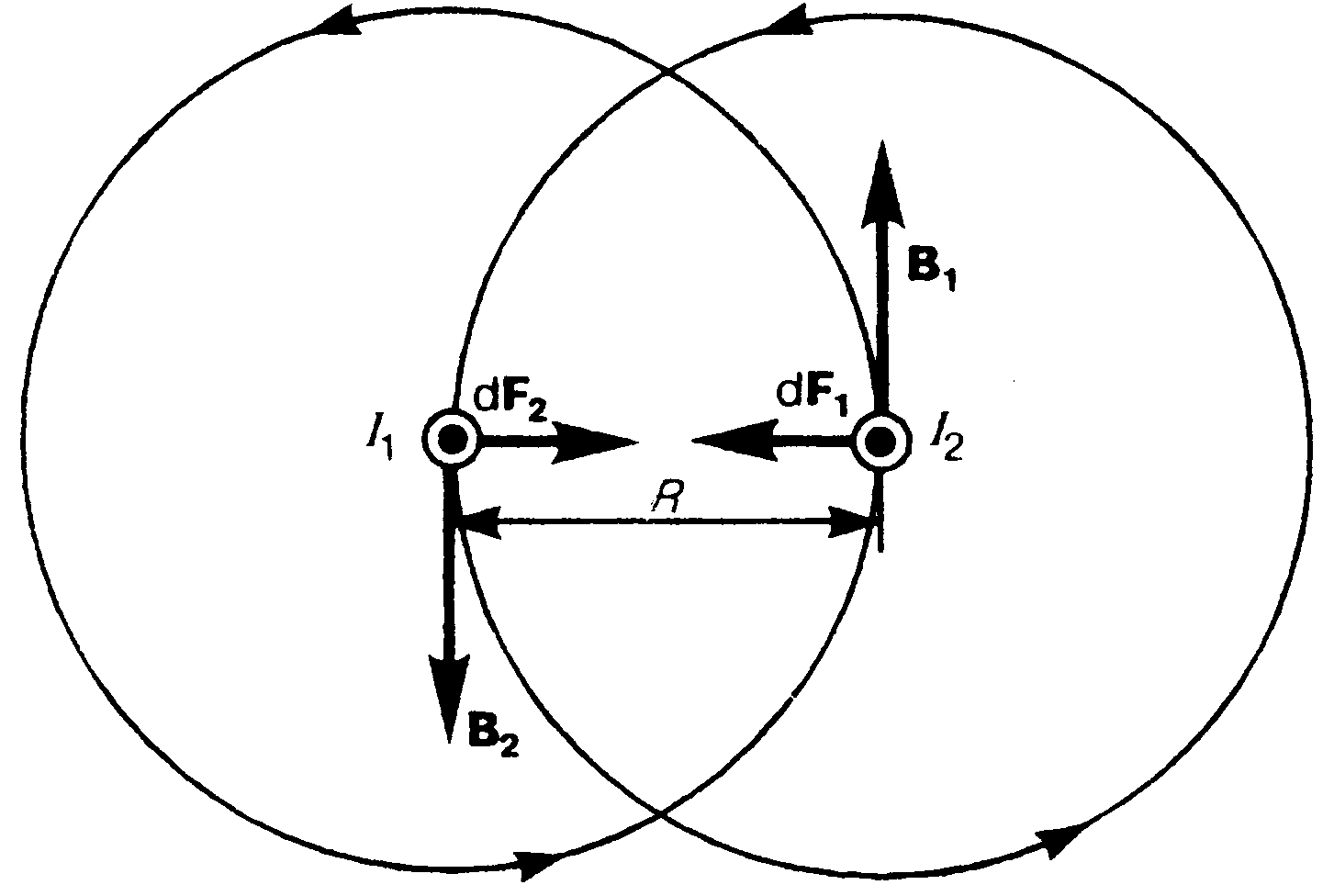Рис. 4

где dl – вектор, по модулю равный dl и совпадающий по направлению с током, B – вектор магнитной индукции. Направление вектора dF может быть найдено по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Два параллельных тока одинакового направления притягиваются друг к другу с силой (рис. 4)

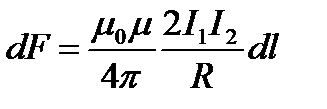, (8)

где R – расстояние между проводниками с токами I₁ и I₂. Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (8).

Рис. 5

Любой движущийся в вакууме или среде заряд создает вокруг себя магнитное поле. Под свободным движением заряда понимается его движение с постоянной скоростью. Закон, определяющий поле В точечного заряда Q, свободно движущегося с нерелятивистской скоростью v, выражается формулой:

, (9)

где r – радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис. 5).

Модуль магнитной индукции вычисляется по формуле

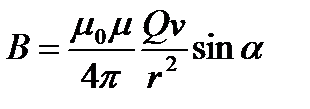, (10)

где a – угол между векторами v и r.

Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная

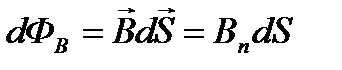, (11)

где 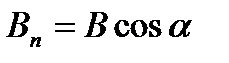– проекция вектора В на направление нормали к площадке dS (a - угол между векторами n и B), dS=dSn – вектор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке.

Поток вектора магнитной индукции через произвольную поверхность S равен

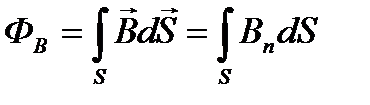. (12)

Для однородного поля и плоской поверхности, расположенной перпендикулярно вектору В, 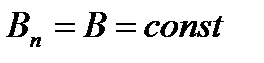и

.

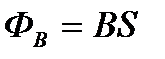Из этой формулы определяется единица магнитного потока – вебер (Вб): 1 Вб – магнитный поток, проходящий сквозь плоскую поверхность площадью 1 м², расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1 Тл.

Теорема Гаусса для поля В: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

. (13)

Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Теорема о циркуляции для поля В. Поле соленоида и тороида.

Циркуляцией вектора В по заданному замкнутому контуру называется интеграл

,

где dl – вектор элементарной длины контура, направленной вдоль обхода контура, 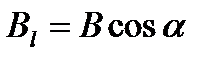– составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), a - угол между векторами dl и B.

Закон полного тока для магнитного поля в вакууме (теорема о циркуляции вектора В): циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m₀ на алгебраическую сумму токов, охватываемых этим контуром:

, (14)

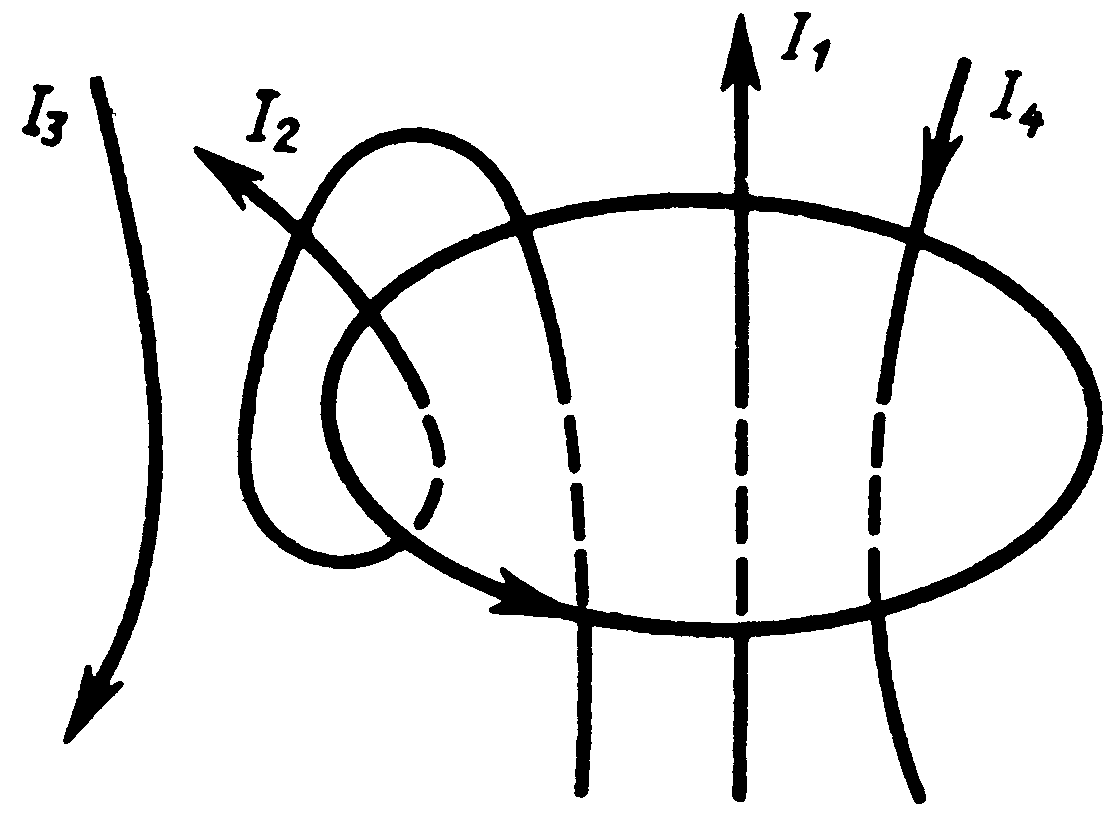Рис. 6

где n – число проводников с токам, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным. Например, для системы токов, изображенных на рис. 6,

.

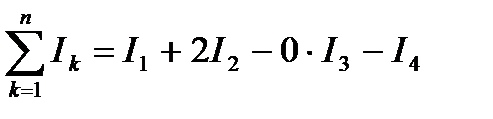Выражение (14) справедливо только для поля в вакууме, поскольку для поля в веществе необходимо учитывать молекулярные токи.

Сравнивая выражения для циркуляции векторов Е и В, видно принципиальное различие: циркуляция вектора Е электростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляция вектора В магнитного поля не равна нулю, такое поле называется вихревым.

С помощью теоремы о циркуляции можно вычислить магнитные поля, создаваемые соленоидом и тороидом. Соленоид – равномерно намотанная на цилиндрическую поверхность проволочная спираль, по которой течет электрический ток. Если катушка длиной l состоит из N витков, по которым течет ток I, то поле внутри нее будет вычисляться по формуле:

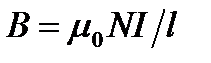. (15)

Тороид – кольцевая катушка, витки которой намотаны на сердечник, имеющий форму тора. Для него поле определяется:

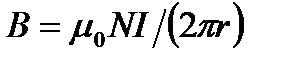, (16)

где r – радиус оси тора.

Следует отметить, что поле внутри соленоида и тороида однородно (краевыми эффектами при расчетах пренебрегают).

Магнитный момент контура с током

При исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта. В магнитном поле рамка с током испытывает ориентирующее действие, т.к. на него действует пара сил Ампера. Вращающий момент зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой:

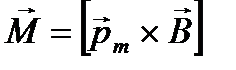, (17)

где p_m – вектор магнитного момента с током. Для плоского контура с током I

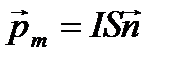, (18)

где S – площадь поверхности контура (рамки), n – единичный вектор нормали к поверхности рамки. Направление p_m совпадает с n.

Формула (17) справедлива для контура с током, находящемся в однородном магнитном поле, независимо от формы этого контура. Если контур с током находится в неоднородном магнитном поле, то действие сил Ампера на контур не сводится только к результирующему моменту. В этом случае на контур действует еще и результирующая сила

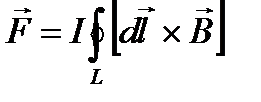, (19)

где интегрирование ведется по всем участкам замкнутого контура L с током I; В – магнитная индукция внешнего магнитного поля, т.к. для собственного магнитного поля контура F=0. Можно показать, что для силы F также справедлива формула

, (20)

где – оператор набла.

На основе взаимодействия тока и магнитного поля в системе СИ устанавливается единица силы тока – ампер. Один ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2×10^-7 Н.

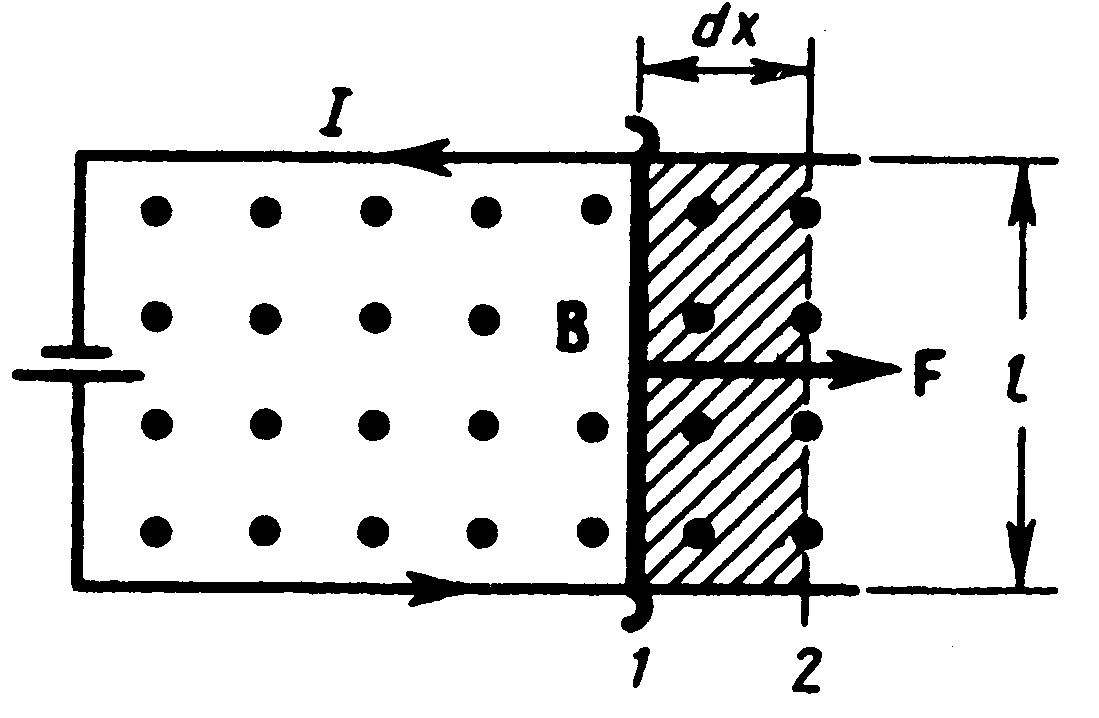Рис. 7

Работа по перемещению проводника в магнитном поле

На проводник с током в магнитном поле действуют силы Ампера, под действием которых он может перемещаться, т.е. магнитное поле способно совершать работу. Для ее определения рассмотрим проводник длиной l с током I, помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура (рис. 7). Под действием силы Ампера 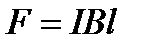проводник переместится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

,

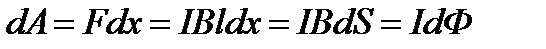Рис. 8

так как – площадь, пересекаемая проводником при его перемещении в магнитном поле, 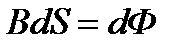– поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,

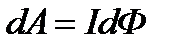, (21)

т.е. работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.

Найдем работу сил Ампера при перемещении в магнитном поле замкнутого контура с током I. Пусть в результате малого перемещения контур перешел от положения С в положение С’ (рис. 8). При этом малый элемент dl контура совершил перемещение dr и прочертил малую площадку dS. Искомая работа сил Ампера при малом перемещении контура определяется формулой

,

где dФ_m – магнитный поток через поверхность, прочерченную контуром. Таким образом работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром. Последняя формула остается справедливой для контура любой формы в произвольном магнитном поле.

Движение заряженных частиц в электрических и магнитных полях

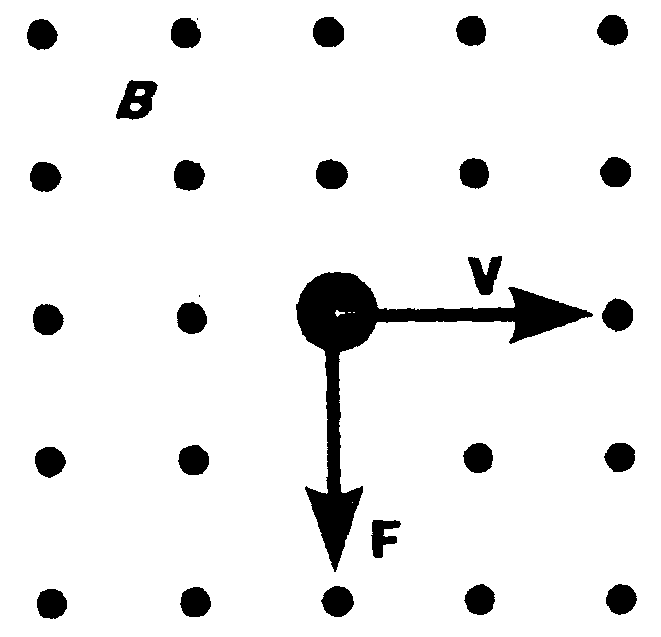Рис. 9

Опыт показывает, что магнитное поле действует не только на проводники с током, но и на отдельные заряды, движущиеся в магнитном поле. Сила, действующая на электрический заряд Q, движущийся в магнитном поле В со скоростью v, называется силой Лоренца и выражается формулой

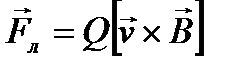. (22)

Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v, то отогнутый большой палец покажет направление силы, действующей на положительный заряд (рис. 9). Модуль силы Лоренца равен

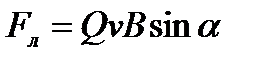. (23)

Магнитное поле действует только на движущиеся в нем заряды. Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает.

Если на движущийся заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил – кулоновской силы и силы Лоренца:

. (24)

Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

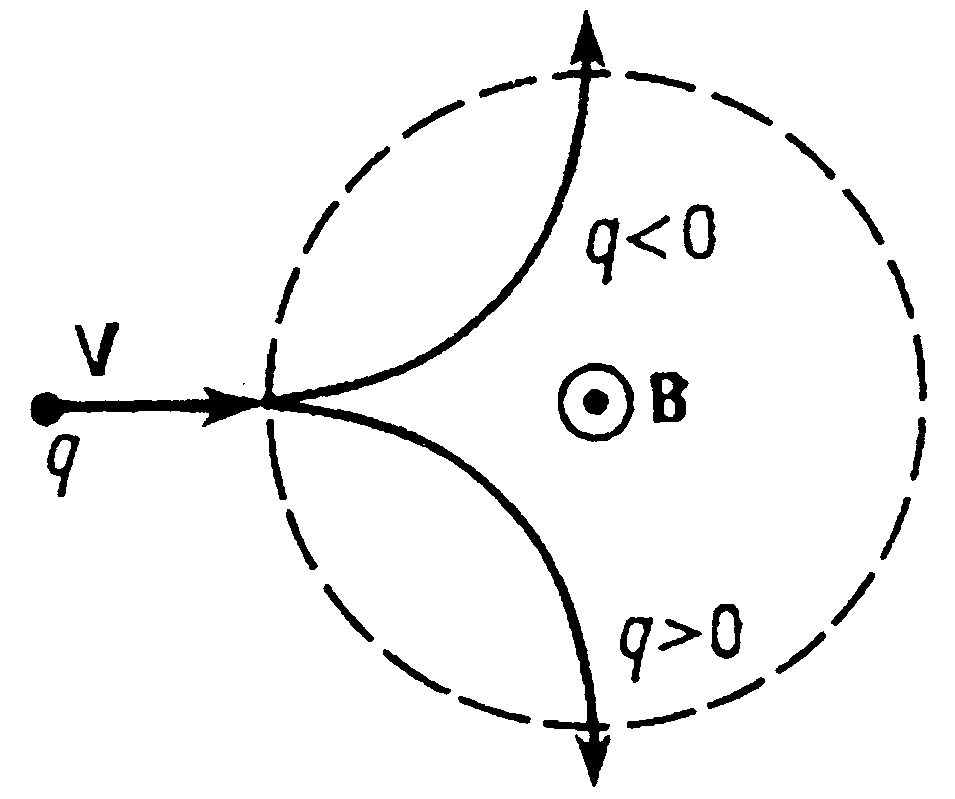Рис. 10

В однородном электрическом поле заряженная частица приобретает (или теряет) кинетическую энергию, что выражается в увеличении (или уменьшении) скорости ее движения. Рассмотрим движение заряженных частиц в однородных магнитных полях.

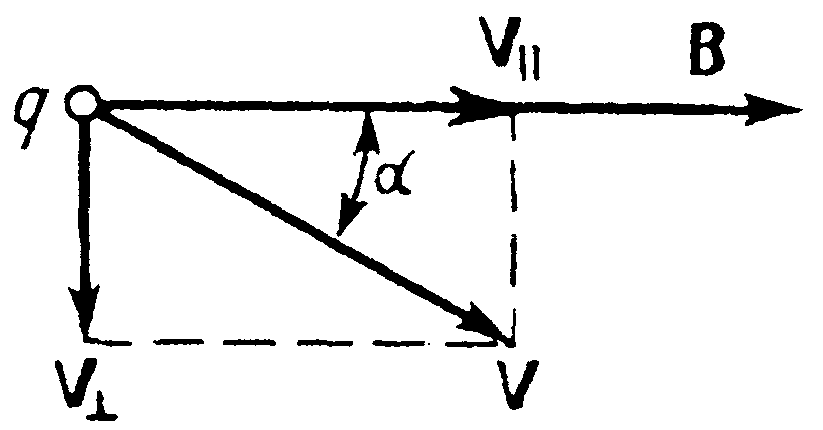
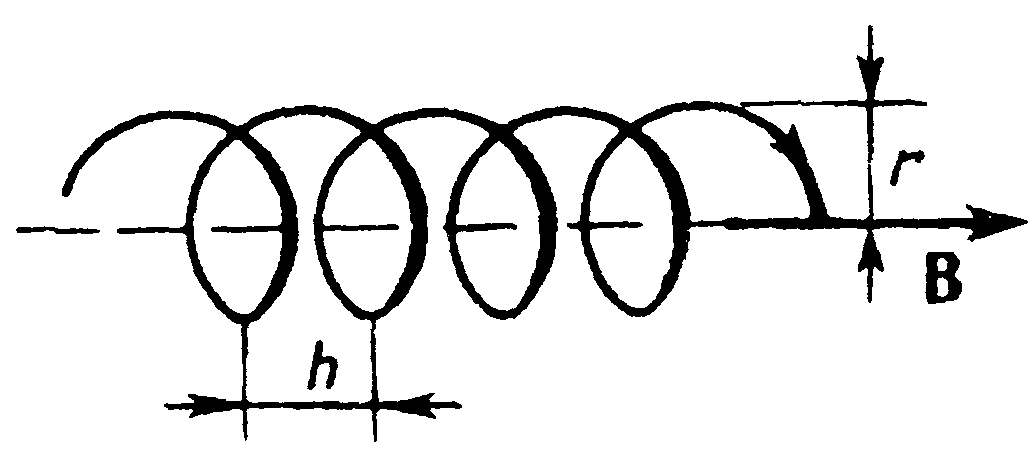Рис. 11

Если частица влетает в магнитное поле так, что ее скорость направлена вдоль линии магнитной индукции (a=0 или p), то сила Лоренца равна 0, т.е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно. Если частица влетает в магнитное поле в направлении перпендикулярном линиям магнитной индукции, то сила Лоренца постоянна по модулю и нормальна к траектории частицы. Под действием силы Лоренца эта траектория искривляется – частица начинает двигаться по дуге окружности (рис. 10), радиус r которой определяется из условия 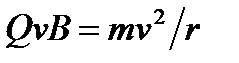, откуда

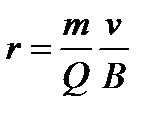, (25)

где m – масса частицы, Q/m – ее удельный заряд. Период обращения частицы вычисляется

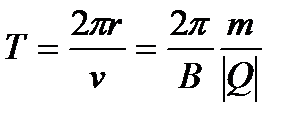. (26)

Если скорость заряженной частицы направлена под углом a к вектору В, то ее движение можно представить в виде суперпозиции: 1) равномерного прямолинейного движения вдоль поля со скоростью ; 2) равномерного движения со скоростью 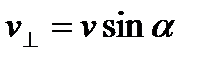по окружности в плоскости, перпендикулярной полю. В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 11). Радиус вращения определяется по формуле (25), где v заменяем на 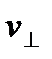. Шаг винтовой линии определится

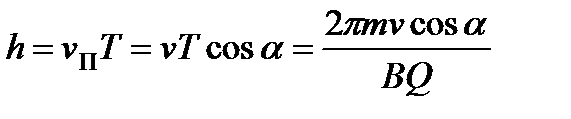. (27)

Использование движения заряженных частиц в электрических

и магнитных полях.

Описанные выше движения заряженных частиц в однородных электрических и магнитных полях лежат в основе многих физических явлений. Рассмотрим лишь некоторые.

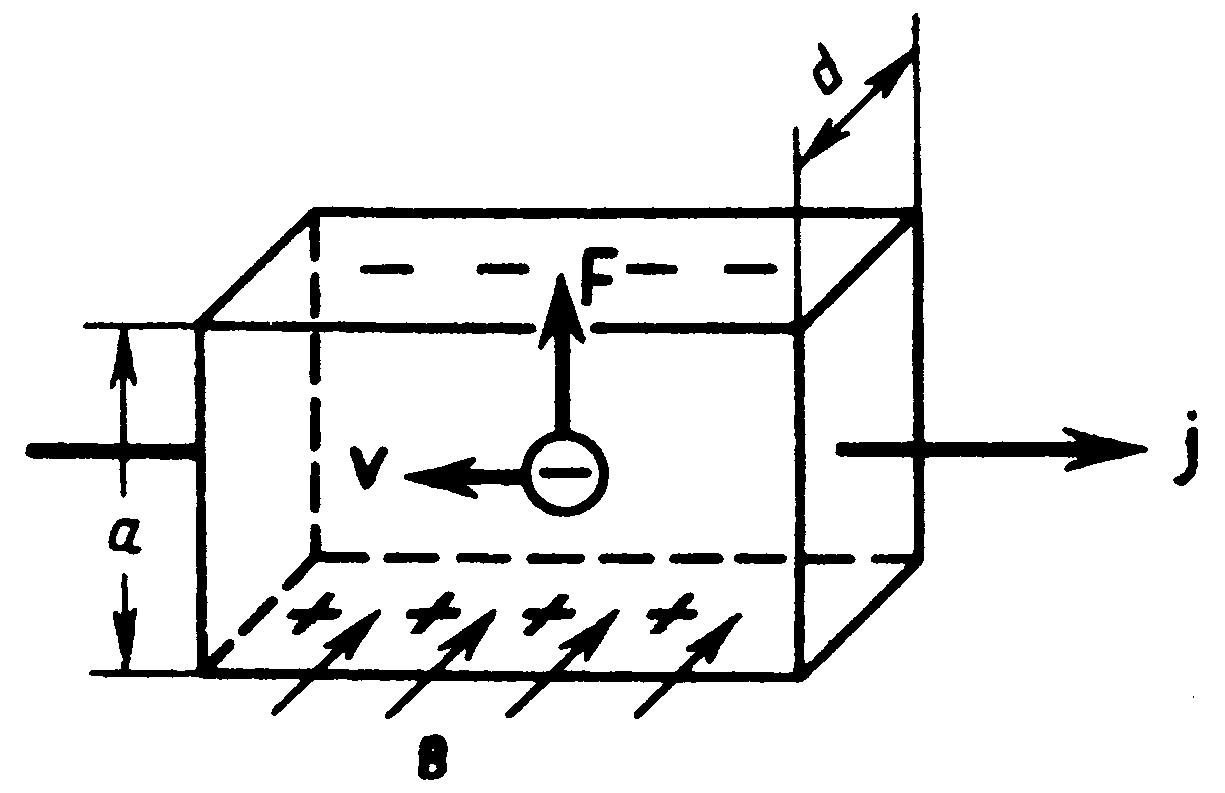Рис. 12

1) Эффект Холла – возникновение в металле (или полупроводнике) с током плотностью j, помещенном в магнитное поле В, электрического поля в направлении, перпендикулярном B и j. Поместим металлическую пластинку с током плотностью j в магнитное поле В, перпендикулярное j (рис. 12). При данном направлении j скорость носителей тока в металле – электронов – направлена справа налево. Электроны испытывают действие силы Лоренца, которая в данном случае направлена вверх. Таким образом, у верхнего края пластинки возникает повышенная концентрация электронов (он зарядится отрицательно), а у нижнего – их недостаток (зарядится положительно). В результате этого между краями пластинки возникает дополнительное поперечное электрическое поле, направленное снизу вверх. Поперечная (холловская) разность потенциалов определится

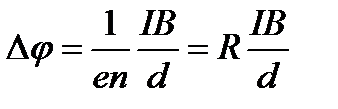, (28)

где d – толщина пластинки, I – сила тока, В – магнитная индукция, 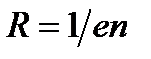- постоянная Холла, зависящая от вещества. По измеренному значению постоянной Холла можно: 1) определить концентрацию носителей тока в проводнике (при известном характере проводимости и заряде носителей); 2) судить о природе проводимости полупроводников, т.к. знак постоянной Холла совпадает со знаком заряда е носителей тока. Эффект Холла также применяется для умножения постоянных токов в аналоговых вычислительных машинах, в измерительной технике (датчики Холла) и т.д.

2) На основе анализа результатов опытов с катодными лучами (по их отклонению в электрическом и магнитном полях, а также по их сравнительно малому ослаблению при прохождении через газы) Томсон пришел к выводу, что катодные лучи не зависят от материала катода и представляют собой поток одних и тех же заряженных отрицательных частиц, причем их размер во много раз меньше размеров атомов. Так была открыта первая в истории элементарная частица – электрон.

3) Для измерения удельных зарядов положительных ионов использовался метод скрещенных полей. Каналовые лучи пропускались через плоский конденсатор, помещенный между полюсами электромагнита так, что направления векторов Е и В совпадали или были противоположны друг другу. В результате совместного действия электрического и магнитных полей положительные ионы, образующие каналовые лучи, отклонялись как в вертикальном, так и в поперечном направлениях, распределяясь по ветвям параболы, ось которой параллельна векторам Е и В. Различным точкам параболы соответствуют ионы, обладающие различными скоростями. Чем больше скорость иона, тем слабее он отклоняется в электрическом и магнитных полях. Ионам с различными удельными зарядами соответствуют разные параболы. При пропускании лучей, состоящих из ионов одного вещества, получают картинки из нескольких парабол, что является доказательством существования изотопов – различных по своей массе атомов одного и того же химического элемента. Приборы, позволяющие измерять удельные заряды ионов и соответственно их массы с высокой степенью точности, называют масс-спектрометры.

4) Ускорителями заряженных частиц называют устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т.д.). В современных мощных ускорителях заряженная частица многократно проходит через электрическое поле, каждый раз увеличивая свою энергию от нескольких тысяч до нескольких сотен тысяч электрон-вольт. Для управления движением частиц и периодического возвращения их в область ускоряющего электрического поля применяется сильное поперечное магнитное поле.

5) Электронно-лучевая трубка (ЭЛТ) – вакуумный прибор, служащий для преобразования в видимое изображение различных электрических сигналов. Для этого в ЭЛТ присутствует электронная пушка, служащая для выработки узконаправленного пучка электронов. Изменение направления луча в ЭЛТ происходит при пропускании пучка через систему управляемых конденсаторов или электромагнитов. При попадании пучка электронов на участок экрана, покрытого люминофором, происходит его свечение.

Лекция 4