Волны в однородных изотропных средах
Спроецируем уравнение Максвелла
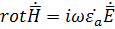 и
и 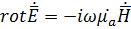 на оси декартовый системы координат. Получим систему скалярных уравнений
на оси декартовый системы координат. Получим систему скалярных уравнений
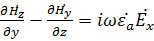
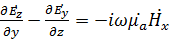
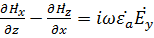
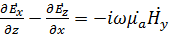
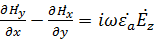 с
с 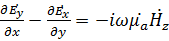
Напряженность магнитного поля можно вычислить из второго уравнения Максвелла 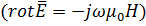 подставив в него полученные выше составляющие вектора
подставив в него полученные выше составляющие вектора 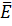 то есть,
то есть, 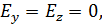 а
а 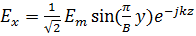 . При этом
. При этом
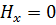
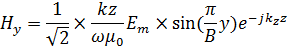
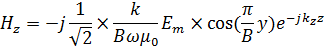
Решение для вектора электрического поля
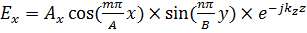
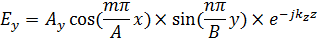
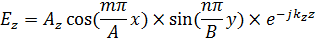
Будут удовлетворять уравнениям Максвелла только в том случае, если
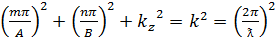 ,
,
где 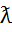 - длина волны в свободном пространстве (6)
- длина волны в свободном пространстве (6)
Из (6) следует что
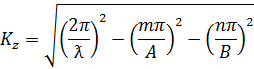
В направлении оси волновода уравнение поля определяется множителем 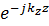 . Для того чтобы в этом направлении поле представляло собой незатухающую бегущую волну необходимо, чтобы
. Для того чтобы в этом направлении поле представляло собой незатухающую бегущую волну необходимо, чтобы 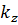 было действительным числом, то есть подкоренным выражением (7) было положительным числом, а это значит, что по волноводу нельзя передавать энергию на частотах, лежащих ниже некоторой критической частоты.
было действительным числом, то есть подкоренным выражением (7) было положительным числом, а это значит, что по волноводу нельзя передавать энергию на частотах, лежащих ниже некоторой критической частоты.
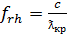 ,
,
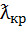 - критическая длина волны
- критическая длина волны
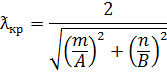
Критическая длина волны определяется из условий равенства нулю подкоренного выражения (7).
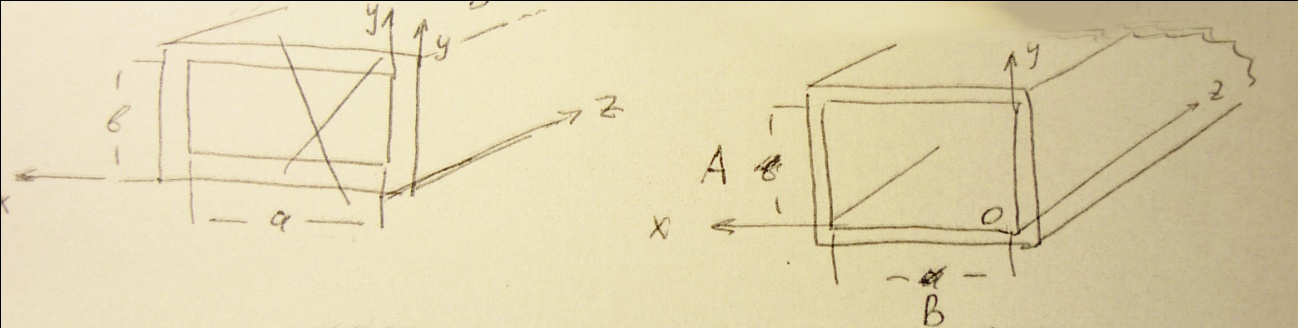
Для определения поля в каком волноводе в общем случае необходимо решить уравнение Максвелла или соответствующие волновые уравнения. При этом решение ищут в той системе координат, координатные поверхности которой по форме подобны внутренним поверхностям волновода. Рассмотрим электромагнитное поле частоты 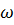 в бесконечно длинном прямоугольном регулярном волноводе с металлическими проводящими стенками, заполненными идеальными диэлектриком с параметром
в бесконечно длинном прямоугольном регулярном волноводе с металлическими проводящими стенками, заполненными идеальными диэлектриком с параметром 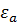 и
и 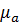 . Задачу решаем в прямоугольной системе координат. Положим, что в рассматриевом объеме нет сторонних токов и свободных зарядов. Тогда волновое уравнение для
. Задачу решаем в прямоугольной системе координат. Положим, что в рассматриевом объеме нет сторонних токов и свободных зарядов. Тогда волновое уравнение для 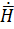 запишется в виде
запишется в виде 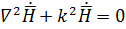 , где
, где 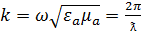 – волновое число диэлектрика, заполняемого волновод.
– волновое число диэлектрика, заполняемого волновод.
Окончательным решение для электрических и магнитных полей имеют вид волны 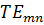
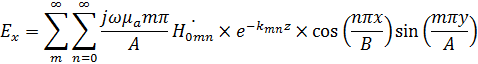
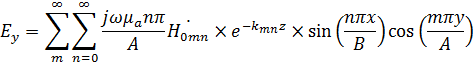
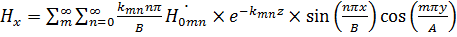 (8)
(8)
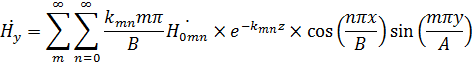
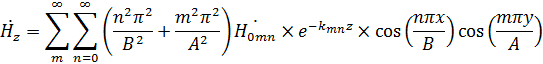
где 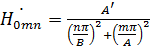 ;
;
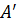 - постоянная, зависящая от интенсивности сторонних источников.
- постоянная, зависящая от интенсивности сторонних источников.
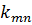 - коэффициент распространения.
- коэффициент распространения.
Из (8) следует, что одной угловой частоте 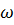 соответствует бесконечное число полей поперечно-электрического типа. Каждый вид поля определяется собственными значениями
соответствует бесконечное число полей поперечно-электрического типа. Каждый вид поля определяется собственными значениями 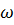 и ƛ .Теоретически все виды полей могут возбуждаться и существовать одновременно ,однако большая часть частных полей затухает в волноводе. Чтобы в волноводе была волна определенной длины её длина должна быть меньше критической.
и ƛ .Теоретически все виды полей могут возбуждаться и существовать одновременно ,однако большая часть частных полей затухает в волноводе. Чтобы в волноводе была волна определенной длины её длина должна быть меньше критической.
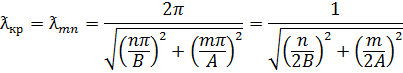
Критическая частота 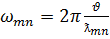
В направлении осей x и y 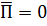 ,так как составляющая
,так как составляющая  сдвинута по фазе
сдвинута по фазе  относительно
относительно 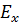 и
и 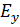 . Таким образом энергия распространяется лишь вдоль волновода: в поперечном же направлении происходит лишь колебании энергии вдоль стоячей волны .
. Таким образом энергия распространяется лишь вдоль волновода: в поперечном же направлении происходит лишь колебании энергии вдоль стоячей волны .
Длина волны в волноводе определяется соотношением
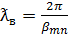 , где
, где 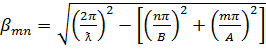 ,
,
где 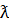 -длинна волны на частоте f в свободном пространстве .
-длинна волны на частоте f в свободном пространстве .
обозначая 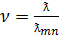
фазовая скорость волны в волноводе:
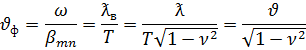
Если волновод заполнен воздухом , то фазовая скорость аналогична фазовой скорости волновода, образованного параллельными идеально проводящими плоскостями оказывается больше предельной скорости- скорости света в вакууме. Передача же сигнала происходит со скоростью 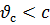 , при этом передача сигнала оценивается групповой скоростью
, при этом передача сигнала оценивается групповой скоростью
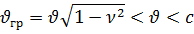
Зависимость фазовой и групповой скорости определяется выражением 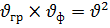
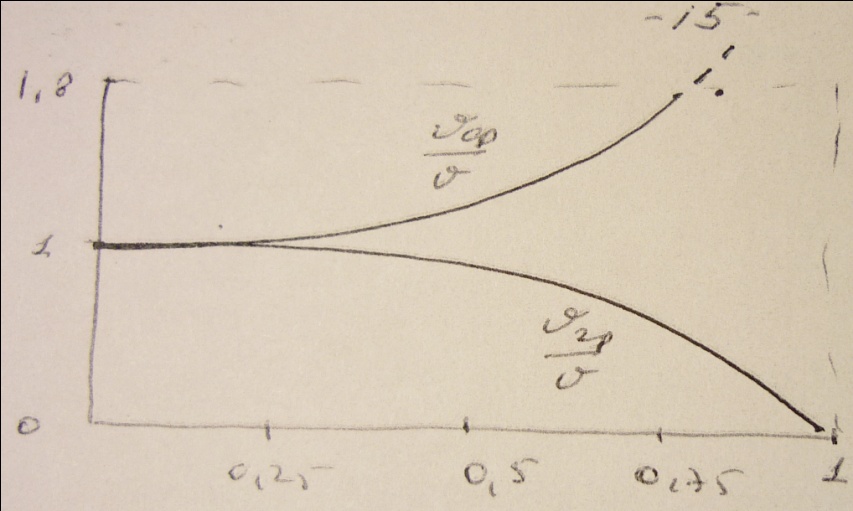
где ƛ-длина волны в свободном пространстве; 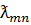 -длина волны m и n- типа.
-длина волны m и n- типа.
Колебание, которому соответствует наибольшая критическая длина волны, называется основным колебанием. Наибольшая критическая длина волны получается при наименьшем значении m и n. Однако волна 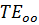 существовать не может так как все составляющие напряженностей поля при m=0 и n=0 равны 0.Наименьшими значениями m и n при которых напряженности E и H отличны от нуля m=1 и n=0. Это колебание
существовать не может так как все составляющие напряженностей поля при m=0 и n=0 равны 0.Наименьшими значениями m и n при которых напряженности E и H отличны от нуля m=1 и n=0. Это колебание 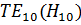 и m=0 n=1 это колебание
и m=0 n=1 это колебание 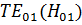 .
.
Для волны 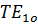 составляющие напряженностей поля определяются при
составляющие напряженностей поля определяются при 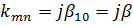
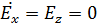
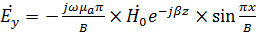
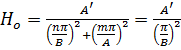
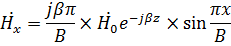
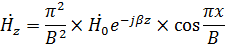
Дата добавления: 2015-12-16; просмотров: 1087;
